1、對卷積的困惑

卷積這個概念，很早以前就學過，但是一直沒有搞懂。教科書上通常會給出定義，給出很多性質，也會用實例和圖形進行解釋，但究竟為什么要這么設計，這么計算，背后的意義是什么，往往語焉不詳。作為一個學物理出身的人，一個公式倘若倘若給不出結合實際的直觀的通俗的解釋（也就是背后的“物理”意義），就覺得少了點什么，覺得不是真的懂了。

教科書上一般定義函數?f, g?的卷積?f * g(n)?如下：

連續形式：

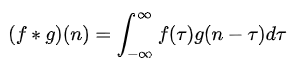
離散形式：

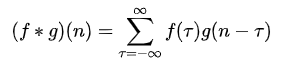
并且也解釋了，先對g函數進行翻轉，相當于在數軸上把g函數從右邊褶到左邊去，也就是卷積的“卷”的由來。

然后再把g函數平移到n，在這個位置對兩個函數的對應點相乘，然后相加，這個過程是卷積的“積”的過程。

這個只是從計算的方式上對公式進行了解釋，從數學上講無可挑剔，但進一步追問，為什么要先翻轉再平移，這么設計有何用意？還是有點費解。

在知乎，已經很多的熱心網友對卷積舉了很多形象的例子進行了解釋，如卷地毯、丟骰子、打耳光、存錢等等。讀完覺得非常生動有趣，但過細想想，還是感覺有些地方還是沒解釋清楚，甚至可能還有瑕疵，或者還可以改進（這些后面我會做一些分析）。

帶著問題想了兩個晚上，終于覺得有些問題想通了，所以就寫出來跟網友分享，共同學習提高。不對的地方歡迎評論拍磚。。。

明確一下，這篇文章主要想解釋兩個問題：

1. 卷積這個名詞是怎么解釋？“卷”是什么意思？“積”又是什么意思？

2. 卷積背后的意義是什么，該如何解釋？

2、考慮的應用場景

為了更好地理解這些問題，我們先給出兩個典型的應用場景：

1. 信號分析

一個輸入信號f(t)，經過一個線性系統（其特征可以用單位沖擊響應函數g(t)描述）以后，輸出信號應該是什么？實際上通過卷積運算就可以得到輸出信號。

2. 圖像處理

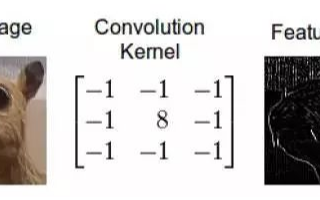
輸入一幅圖像f(x,y)，經過特定設計的卷積核g(x,y)進行卷積處理以后，輸出圖像將會得到模糊，邊緣強化等各種效果。

3、對卷積的理解

對卷積這個名詞的理解：所謂兩個函數的卷積，本質上就是先將一個函數翻轉，然后進行滑動疊加。

在連續情況下，疊加指的是對兩個函數的乘積求積分，在離散情況下就是加權求和，為簡單起見就統一稱為疊加。

整體看來是這么個過程：

翻轉——>滑動——>疊加——>滑動——>疊加——>滑動——>疊加.....

多次滑動得到的一系列疊加值，構成了卷積函數。

卷積的“卷”，指的的函數的翻轉，從?g(t)?變成?g(-t)?的這個過程；同時，“卷”還有滑動的意味在里面（吸取了網友李文清的建議）。如果把卷積翻譯為“褶積”，那么這個“褶”字就只有翻轉的含義了。

卷積的“積”，指的是積分/加權求和。

有些文章只強調滑動疊加求和，而沒有說函數的翻轉，我覺得是不全面的；有的文章對“卷”的理解其實是“積”，我覺得是張冠李戴。

對卷積的意義的理解：

1. 從“積”的過程可以看到，我們得到的疊加值，是個全局的概念。以信號分析為例，卷積的結果是不僅跟當前時刻輸入信號的響應值有關，也跟過去所有時刻輸入信號的響應都有關系，考慮了對過去的所有輸入的效果的累積。在圖像處理的中，卷積處理的結果，其實就是把每個像素周邊的，甚至是整個圖像的像素都考慮進來，對當前像素進行某種加權處理。所以說，“積”是全局概念，或者說是一種“混合”，把兩個函數在時間或者空間上進行混合。

2. 那為什么要進行“卷”？直接相乘不好嗎？我的理解，進行“卷”（翻轉）的目的其實是施加一種約束，它指定了在“積”的時候以什么為參照。在信號分析的場景，它指定了在哪個特定時間點的前后進行“積”，在空間分析的場景，它指定了在哪個位置的周邊進行累積處理。

4、舉例說明

下面舉幾個例子說明為什么要翻轉，以及疊加求和的意義。

例1：信號分析

如下圖所示，輸入信號是?f(t)?，是隨時間變化的。系統響應函數是?g(t)?，圖中的響應函數是隨時間指數下降的，它的物理意義是說：如果在?t=0 的時刻有一個輸入，那么隨著時間的流逝，這個輸入將不斷衰減。換言之，到了?t=T時刻，原來在?t=0 時刻的輸入f(0)的值將衰減為f(0)g(T)。

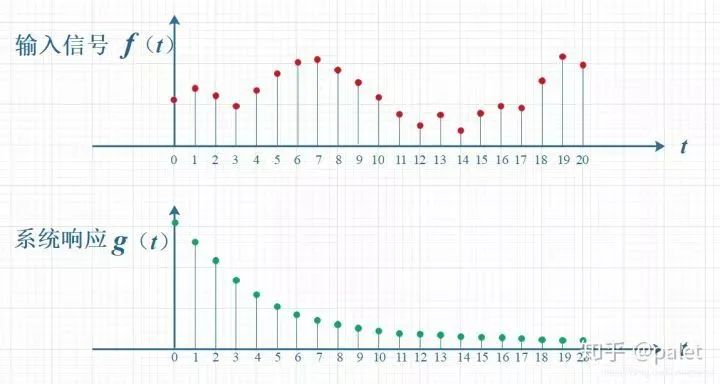
考慮到信號是連續輸入的，也就是說，每個時刻都有新的信號進來，所以，最終輸出的是所有之前輸入信號的累積效果。如下圖所示，在T=10時刻，輸出結果跟圖中帶標記的區域整體有關。其中，f(10)因為是剛輸入的，所以其輸出結果應該是f(10)g(0)，而時刻t=9的輸入f(9)，只經過了1個時間單位的衰減，所以產生的輸出應該是 f(9)g(1)，如此類推，即圖中虛線所描述的關系。這些對應點相乘然后累加，就是T=10時刻的輸出信號值，這個結果也是f和g兩個函數在T=10時刻的卷積值。

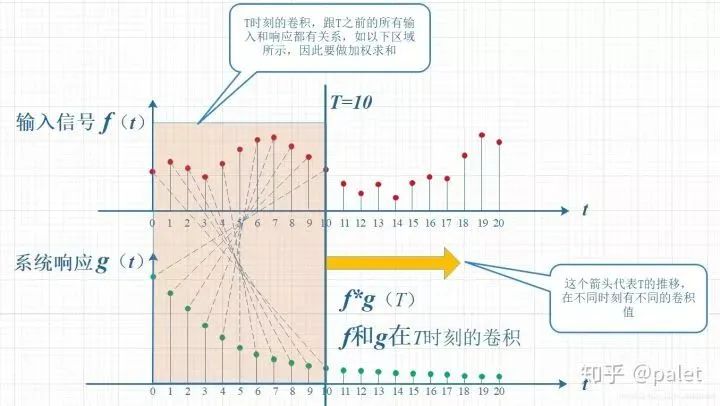
顯然，上面的對應關系看上去比較難看，是擰著的，所以，我們把g函數對折一下，變成了g(-t)，這樣就好看一些了。看到了嗎？這就是為什么卷積要“卷”，要翻轉的原因，這是從它的物理意義中給出的。

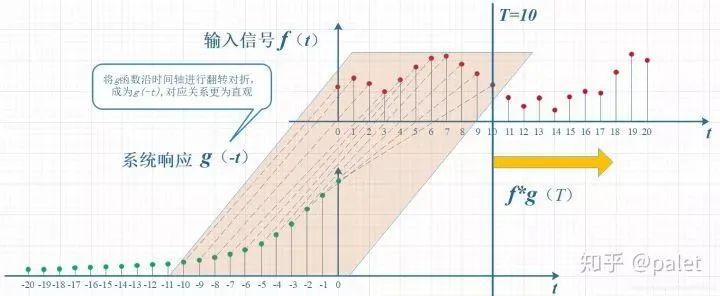
上圖雖然沒有擰著，已經順過來了，但看上去還有點錯位，所以再進一步平移T個單位，就是下圖。它就是本文開始給出的卷積定義的一種圖形的表述：

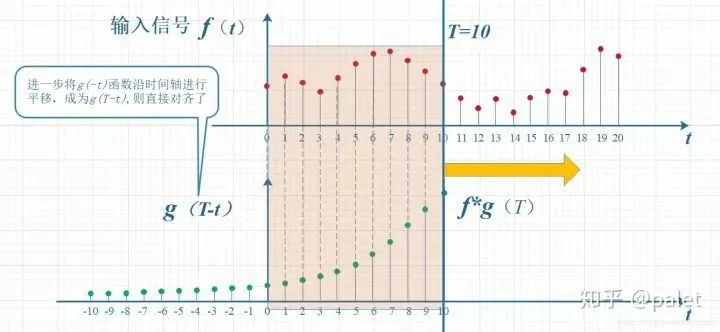
所以，在以上計算T時刻的卷積時，要維持的約束就是：t+ (T-t) = T??。這種約束的意義，大家可以自己體會。

例2：丟骰子

在本問題?如何通俗易懂地解釋卷積？中排名第一的馬同學在中舉了一個很好的例子（下面的一些圖摘自馬同學的文章，在此表示感謝），用丟骰子說明了卷積的應用。

要解決的問題是：有兩枚骰子，把它們都拋出去，兩枚骰子點數加起來為4的概率是多少?

分析一下，兩枚骰子點數加起來為4的情況有三種情況：1+3=4， 2+2=4, 3+1=4

因此，兩枚骰子點數加起來為4的概率為：

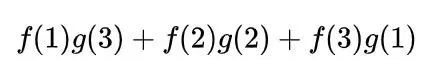
寫成卷積的方式就是：

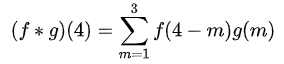
在這里我想進一步用上面的翻轉滑動疊加的邏輯進行解釋。

首先，因為兩個骰子的點數和是4，為了滿足這個約束條件，我們還是把函數 g 翻轉一下，然后陰影區域上下對應的數相乘，然后累加，相當于求自變量為4的卷積值，如下圖所示：

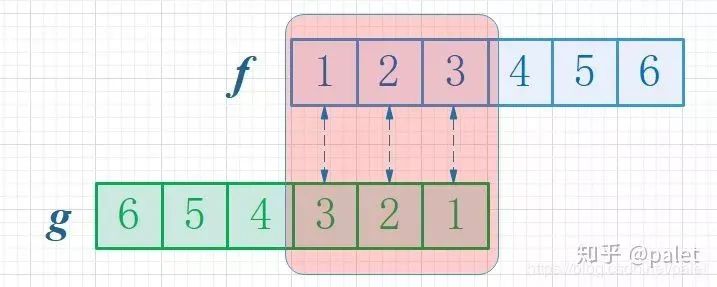
進一步，如此翻轉以后，可以方便地進行推廣去求兩個骰子點數和為 n 時的概率，為f 和 g的卷積 f*g(n)，如下圖所示：

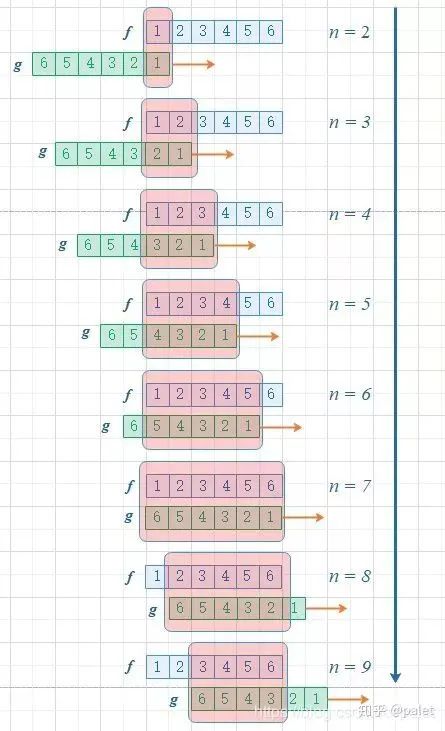
由上圖可以看到，函數 g 的滑動，帶來的是點數和的增大。這個例子中對f和g的約束條件就是點數和，它也是卷積函數的自變量。有興趣還可以算算，如果骰子的每個點數出現的概率是均等的，那么兩個骰子的點數和n=7的時候，概率最大。

例3：圖像處理

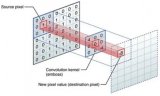
還是引用知乎問題?如何通俗易懂地解釋卷積？中馬同學的例子。圖像可以表示為矩陣形式（下圖摘自馬同學的文章）：

對圖像的處理函數（如平滑，或者邊緣提取），也可以用一個g矩陣來表示，如：

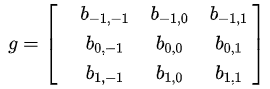
注意，我們在處理平面空間的問題，已經是二維函數了，相當于：

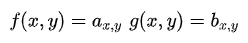
那么函數f和g的在（u，v）處的卷積該如何計算呢？

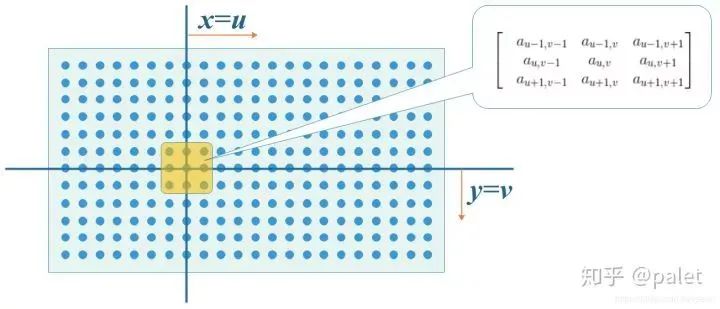
首先我們在原始圖像矩陣中取出（u,v）處的矩陣：

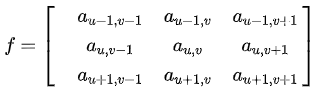
然后將圖像處理矩陣翻轉（這個翻轉有點意思，不是延x軸和y軸兩個方向翻轉，而是沿右上到左下的對角線翻轉，這是為了湊后面的內積公式。），如下：

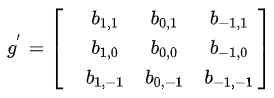
可對比下圖：

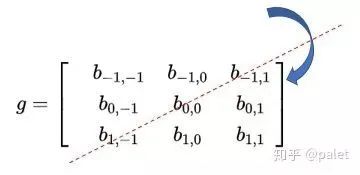
計算卷積時，就可以用和的內積：

?

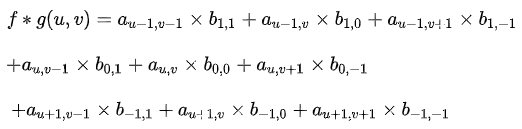
請注意，以上公式有一個特點，做乘法的兩個對應變量a,b的下標之和都是（u,v），其目的是對這種加權求和進行一種約束。這也是為什么要將矩陣g進行翻轉的原因。以上矩陣下標之所以那么寫，并且進行了翻轉，是為了讓大家更清楚地看到跟卷積的關系。這樣做的好處是便于推廣，也便于理解其物理意義。實際在計算的時候，都是用翻轉以后的矩陣，直接求矩陣內積就可以了。

以上計算的是（u,v）處的卷積，延x軸或者y軸滑動，就可以求出圖像中各個位置的卷積，其輸出結果是處理以后的圖像（即經過平滑、邊緣提取等各種處理的圖像）。

再深入思考一下，在算圖像卷積的時候，我們是直接在原始圖像矩陣中取了（u,v）處的矩陣，為什么要取這個位置的矩陣，本質上其實是為了滿足以上的約束。因為我們要算（u，v）處的卷積，而g矩陣是3x3的矩陣，要滿足下標跟這個3x3矩陣的和是（u,v），只能是取原始圖像中以（u，v）為中心的這個3x3矩陣，即圖中的陰影區域的矩陣。

推而廣之，如果如果g矩陣不是3x3，而是6x6，那我們就要在原始圖像中取以（u，v）為中心的6x6矩陣進行計算。由此可見，這種卷積就是把原始圖像中的相鄰像素都考慮進來，進行混合。相鄰的區域范圍取決于g矩陣的維度，維度越大，涉及的周邊像素越多。而矩陣的設計，則決定了這種混合輸出的圖像跟原始圖像比，究竟是模糊了，還是更銳利了。

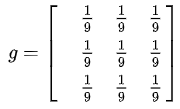
比如說，如下圖像處理矩陣將使得圖像變得更為平滑，顯得更模糊，因為它聯合周邊像素進行了平均處理：

而如下圖像處理矩陣將使得像素值變化明顯的地方更為明顯，強化邊緣，而變化平緩的地方沒有影響，達到提取邊緣的目的：

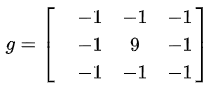
5、對一些解釋的不同意見

上面一些對卷積的形象解釋，如知乎問題?卷積為什么叫「卷」積？中荊哲以及問題?如何通俗易懂地解釋卷積？中馬同學等人提出的如下比喻：

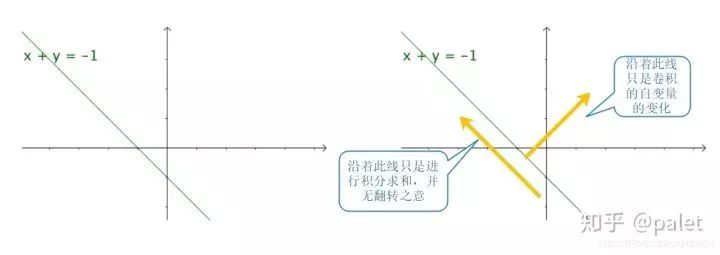
其實圖中“卷”的方向，是沿該方向進行積分求和的方向，并無翻轉之意。因此，這種解釋，并沒有完整描述卷積的含義，對“卷”的理解值得商榷。

審核編輯：黃飛

?