本文是對卷積神經網絡的基礎進行介紹,主要內容包括卷積神經網絡概念、卷積神經網絡結構、卷積神經網絡求解、卷積神經網絡LeNet-5結構分析、卷積神經網絡注意事項。
一、卷積神經網絡概念
上世紀60年代,Hubel等人通過對貓視覺皮層細胞的研究,提出了感受野這個概念,到80年代,Fukushima在感受野概念的基礎之上提出了神經認知機的概念,可以看作是卷積神經網絡的第一個實現網絡,神經認知機將一個視覺模式分解成許多子模式(特征),然后進入分層遞階式相連的特征平面進行處理,它試圖將視覺系統模型化,使其能夠在即使物體有位移或輕微變形的時候,也能完成識別。
卷積神經網絡(Convolutional Neural Networks, CNN)是多層感知機(MLP)的變種。由生物學家休博爾和維瑟爾在早期關于貓視覺皮層的研究發展而來。視覺皮層的細胞存在一個復雜的構造。這些細胞對視覺輸入空間的子區域非常敏感,我們稱之為感受野,以這種方式平鋪覆蓋到整個視野區域。這些細胞可以分為兩種基本類型,簡單細胞和復雜細胞。簡單細胞最大程度響應來自感受野范圍內的邊緣刺激模式。復雜細胞有更大的接受域,它對來自確切位置的刺激具有局部不變性。
通常神經認知機包含兩類神經元,即承擔特征提取的采樣元和抗變形的卷積元,采樣元中涉及兩個重要參數,即感受野與閾值參數,前者確定輸入連接的數目,后者則控制對特征子模式的反應程度。卷積神經網絡可以看作是神經認知機的推廣形式,神經認知機是卷積神經網絡的一種特例。
CNN由紐約大學的Yann LeCun于1998年提出。CNN本質上是一個多層感知機,其成功的原因關鍵在于它所采用的局部連接和共享權值的方式,一方面減少了的權值的數量使得網絡易于優化,另一方面降低了過擬合的風險。CNN是神經網絡中的一種,它的權值共享網絡結構使之更類似于生物神經網絡,降低了網絡模型的復雜度,減少了權值的數量。該優點在網絡的輸入是多維圖像時表現的更為明顯,使圖像可以直接作為網絡的輸入,避免了傳統識別算法中復雜的特征提取和數據重建過程。在二維圖像處理上有眾多優勢,如網絡能自行抽取圖像特征包括顏色、紋理、形狀及圖像的拓撲結構;在處理二維圖像問題上,特別是識別位移、縮放及其它形式扭曲不變性的應用上具有良好的魯棒性和運算效率等。
CNN本身可以采用不同的神經元和學習規則的組合形式。
CNN具有一些傳統技術所沒有的優點:良好的容錯能力、并行處理能力和自學習能力,可處理環境信息復雜,背景知識不清楚,推理規則不明確情況下的問題,允許樣品有較大的缺損、畸變,運行速度快,自適應性能好,具有較高的分辨率。它是通過結構重組和減少權值將特征抽取功能融合進多層感知器,省略識別前復雜的圖像特征抽取過程。
CNN的泛化能力要顯著優于其它方法,卷積神經網絡已被應用于模式分類,物體檢測和物體識別等方面。利用卷積神經網絡建立模式分類器,將卷積神經網絡作為通用的模式分類器,直接用于灰度圖像。
CNN是一個前潰式神經網絡,能從一個二維圖像中提取其拓撲結構,采用反向傳播算法來優化網絡結構,求解網絡中的未知參數。
CNN是一類特別設計用來處理二維數據的多層神經網絡。CNN被認為是第一個真正成功的采用多層層次結構網絡的具有魯棒性的深度學習方法。CNN通過挖掘數據中的空間上的相關性,來減少網絡中的可訓練參數的數量,達到改進前向傳播網絡的反向傳播算法效率,因為CNN需要非常少的數據預處理工作,所以也被認為是一種深度學習的方法。在CNN中,圖像中的小塊區域(也叫做“局部感知區域”)被當做層次結構中的底層的輸入數據,信息通過前向傳播經過網絡中的各個層,在每一層中都由過濾器構成,以便能夠獲得觀測數據的一些顯著特征。因為局部感知區域能夠獲得一些基礎的特征,比如圖像中的邊界和角落等,這種方法能夠提供一定程度對位移、拉伸和旋轉的相對不變性。
CNN中層次之間的緊密聯系和空間信息使得其特別適用于圖像的處理和理解,并且能夠自動的從圖像抽取出豐富的相關特性。
CNN通過結合局部感知區域、共享權重、空間或者時間上的降采樣來充分利用數據本身包含的局部性等特征,優化網絡結構,并且保證一定程度上的位移和變形的不變性。
CNN受視覺神經機制的啟發而設計,是為識別二維或三維信號而設計的一個多層感知器,這種網絡結構對平移、縮放、傾斜等變形具有高度不變性。
CNN可以用來識別位移、縮放及其它形式扭曲不變性的二維或三維圖像。CNN的特征提取層參數是通過訓練數據學習得到的,所以其避免了人工特征提取,而是從訓練數據中進行學習;其次同一特征圖的神經元共享權值,減少了網絡參數,這也是卷積網絡相對于全連接網絡的一大優勢。共享局部權值這一特殊結構更接近于真實的生物神經網絡使CNN在圖像處理、語音識別領域有著獨特的優越性,另一方面權值共享同時降低了網絡的復雜性,且多維輸入信號(語音、圖像)可以直接輸入網絡的特點避免了特征提取和分類過程中數據重排的過程。
CNN是一種特殊的深層的神經網絡模型,它的特殊性體現在兩個方面,一方面它的神經元的連接是非全連接的,另一方面同一層中某些神經元之間的連接的權重是共享的(即相同的)。它的非全連接和權值共享的網絡結構使之更類似于生物神經網絡,降低了網絡模型的復雜度(對于很難學習的深層結構來說,這是非常重要的),減少了權值的數量。
CNN是一種深度的監督學習下的機器學習模型,具有極強的適應性,善于挖掘數據局部特征,提取全局訓練特征和分類,它的權值共享結構網絡使之更類似于生物神經網絡,在模式識別各個領域都取得了很好的成果。
稀疏連接:在BP神經網絡中,每一層的神經元節點是一個線性一維排列結構,層與層各神經元節點之間是全連接的。卷積神經網絡中,層與層之間的神經元節點不再是全連接形式,利用層間局部空間相關性將相鄰每一層的神經元節點只與和它相近的上層神經元節點連接,即局部連接。這樣大大降低了神經網絡架構的參數規模。
權重共享:在卷積神經網絡中,卷積層的每一個卷積濾波器重復的作用于整個感受野中,對輸入圖像進行卷積,卷積結果構成了輸入圖像的特征圖,提取出圖像的局部特征。每一個卷積濾波器共享相同的參數,包括相同的權重矩陣和偏置項。共享權重的好處是在對圖像進行特征提取時不用考慮局部特征的位置。而且權重共享提供了一種有效的方式,使要學習的卷積神經網絡模型參數數量大大降低。
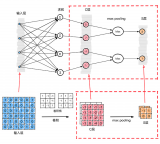
最大池采樣:它是一種非線性降采樣方法。在通過卷積獲取圖像特征之后是利用這些特征進行分類。可以用所有提取到的特征數據進行分類器的訓練,但這通常會產生極大的計算量。所以在獲取圖像的卷積特征后,要通過最大池采樣方法對卷積特征進行降維。將卷積特征劃分為數個n*n的不相交區域,用這些區域的最大(或平均)特征來表示降維后的卷積特征。這些降維后的特征更容易進行分類。
最大池采樣在計算機視覺中的價值體現在兩個方面:(1)、它減小了來自上層隱藏層的計算復雜度;(2)、這些池化單元具有平移不變性,即使圖像有小的位移,提取到的特征依然會保持不變。由于增強了對位移的魯棒性,最大池采樣方法是一個高效的降低數據維度的采樣方法。
Softmax回歸:它是在邏輯回歸的基礎上擴張而來,它的目的是為了解決多分類問題。在這類問題中,訓練樣本的種類一般在兩個以上。Softmax回歸是有監督學習算法,它也可以與深度學習或無監督學習方法結合使用。
CNN是一種帶有卷積結構的深度神經網絡,通常至少有兩個非線性可訓練的卷積層,兩個非線性的固定卷積層(又叫Pooling Laye)和一個全連接層,一共至少5個隱含層。
卷積神經網絡中,輸入就是一幅幅的圖像,權值W就是卷積模板,一般是卷積層和下采樣層交替,最后是全連接的神經網絡。
局部區域感知能夠發現數據的一些局部特征,比如圖片上的一個角,一段弧,這些基本特征是構成動物視覺的基礎。
CNN中每一層的由多個map組成,每個map由多個神經單元組成,同一個map的所有神經單元共用一個卷積核(即權重),卷積核往往代表一個特征,比如某個卷積核代表一段弧,那么把這個卷積核在整個圖片上滾一下,卷積值較大的區域就很有可能是一段弧。注意卷積核其實就是權重,我們并不需要單獨去計算一個卷積,而是一個固定大小的權重矩陣去圖像上匹配時,這個操作與卷積類似,因此我們稱為卷積神經網絡,實際上,BP也可以看作一種特殊的卷積神經網絡,只是這個卷積核就是某層的所有權重,即感知區域是整個圖像。權重共享策略減少了需要訓練的參數,使得訓練出來的模型的泛華能力更強。
CNN一般采用卷積層與采樣層交替設置,即一層卷積層接一層采樣層,采樣層后接一層卷積...這樣卷積層提取出特征,再進行組合形成更抽象的特征,最后形成對圖片對象的描述特征,CNN后面還可以跟全連接層,全連接層跟BP一樣。
CNN的最大特點就是稀疏連接(局部感受)和權值共享。稀疏連接和權值共享可以減少所要訓練的參數,減少計算復雜度。
卷積神經網絡是一個多層的神經網絡,每層由多個二維平面組成,而每個平面由多個獨立神經元組成。
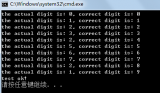
卷積網絡在本質上是一種輸入到輸出的映射,它能夠學習大量的輸入與輸出之間的映射關系,而不需要任何輸入和輸出之間的精確的數學表達式,只要用已知的模式對卷積網絡加以訓練,網絡就具有輸入輸出對之間的映射能力。卷積網絡執行的是有導師訓練,所以其樣本集是由形如:(輸入向量,理想輸出向量)的向量對構成的。所有這些向量對,都應該是來源于網絡即將模擬的系統的實際“運行”結果。它們可以是從實際運行系統中采集來的。在開始訓練前,所有的權都應該用一些不同的小隨機數進行初始化。“小隨機數”用來保證網絡不會因權值過大而進入飽和狀態,從而導致訓練失敗;“不同”用來保證網絡可以正常地學習。實際上,如果用相同的數去初始化權矩陣,則網絡無能力學習。訓練算法與傳統的BP算法差不多。
二、卷積神經網絡結構
卷積神經網絡整體架構:卷積神經網絡是一種多層的監督學習神經網絡,隱含層的卷積層和池采樣層是實現卷積神經網絡特征提取功能的核心模塊。該網絡模型通過采用梯度下降法最小化損失函數對網絡中的權重參數逐層反向調節,通過頻繁的迭代訓練提高網絡的精度。卷積神經網絡的低隱層是由卷積層和最大池采樣層交替組成,高層是全連接層對應傳統多層感知器的隱含層和邏輯回歸分類器。第一個全連接層的輸入是由卷積層和子采樣層進行特征提取得到的特征圖像。最后一層輸出層是一個分類器,可以采用邏輯回歸,Softmax回歸甚至是支持向量機對輸入圖像進行分類。
卷積神經網絡結構包括:卷積層,降采樣層,全鏈接層。每一層有多個特征圖,每個特征圖通過一種卷積濾波器提取輸入的一種特征,每個特征圖有多個神經元。
卷積層:使用卷積層的原因是卷積運算的一個重要特點是,通過卷積運算,可以使原信號特征增強,并且降低噪音。
降采樣層:使用降采樣的原因是,根據圖像局部相關性的原理,對圖像進行子采樣可以減少計算量,同時保持圖像旋轉不變性。
采樣的目的主要是混淆特征的具體位置,因為某個特征找出來后,它的具體位置已經不重要了,我們只需要這個特征與其他的相對位置,比如一個“8”,當我們得到了上面一個"o"時,我們不需要知道它在圖像的具體位置,只需要知道它下面又是一個“o”我們就可以知道是一個'8'了,因為圖片中"8"在圖片中偏左或者偏右都不影響我們認識它,這種混淆具體位置的策略能對變形和扭曲的圖片進行識別。
全連接層:采用softmax全連接,得到的激活值即卷積神經網絡提取到的圖片特征。
卷積層的map個數是在網絡初始化指定的,而卷積層的map的大小是由卷積核和上一層輸入map的大小決定的,假設上一層的map大小是n*n、卷積核的大小是k*k,則該層的map大小是(n-k+1)*(n-k+1)。
采樣層是對上一層map的一個采樣處理,這里的采樣方式是對上一層map的相鄰小區域進行聚合統計,區域大小為scale*scale,有些實現是取小區域的最大值,而ToolBox里面的實現是采用2*2小區域的均值。注意,卷積的計算窗口是有重疊的,而采樣的計算窗口沒有重疊,ToolBox里面計算采樣也是用卷積(conv2(A,K,'valid'))來實現的,卷積核是2*2,每個元素都是1/4,去掉計算得到的卷積結果中有重疊的部分。
CNN的基本結構包括兩種特殊的神經元層,其一為卷積層,每個神經元的輸入與前一層的局部相連,并提取該局部的特征;其二是池化層,用來求局部敏感性與二次特征提取的計算層。這種兩次特征提取結構減少了特征分辨率,減少了需要優化的參數數目。
CNN是部分連接網絡,其最底層是特征提取層(卷積層),接著是池化層(Pooling),然后可以繼續增加卷積、池化或全連接層。用于模式分類的CNN,通常在最后層使用softmax.
一般情況下,CNN的結構形式是:輸入層--> Conv層 --> Pooling層 --> (重復Conv、Pooling層) … --> FC(Full-connected)層 --> 輸出結果。通常輸入層大小一般為2的整數倍,如32,64,96,224,384等。通常卷積層使用較小的filter,如3*3,最大也就5*5。Pooling層用于對卷積結果進行降低維度,例如選擇2*2的區域對卷積層進行降低維度,則選擇2*2區域的最大值作為輸出,這樣卷積層的維度就降為之前一半。
一般地,CNN的基本結構包括兩層,其一為特征提取層,每個神經元的輸入與前一層的局部接受域相連,并提取該局部的特征。一旦該局部特征被提取后,它與其它特征間的位置關系也隨之確定下來;其二是特征映射層,網絡的每個計算層由多個特征映射組成,每個特征映射是一個平面,平面上所有神經元的權值相等。特征映射結構采用影響函數核小的sigmoid函數作為卷積網絡的激活函數,使得特征映射具有位移不變性。此外,由于一個映射面上的神經元共享權值,因而減少了網絡自由參數的個數。卷積神經網絡中的每一個卷積層都緊跟著一個用來求局部平均與二次提取的計算層,這種特有的兩次特征提取結構減小了特征分辨率。
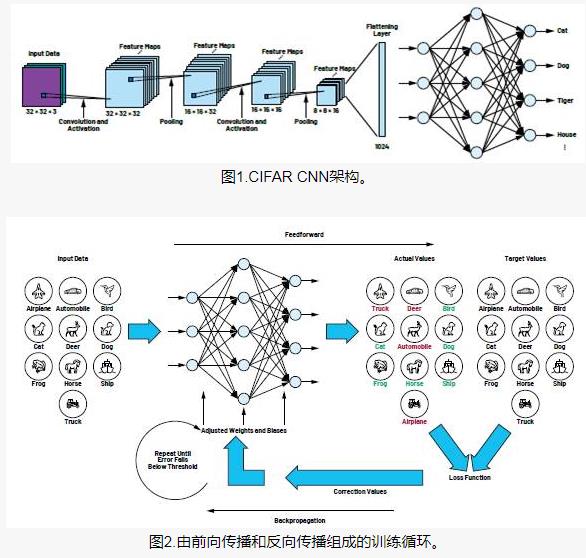
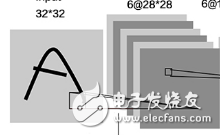
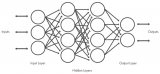
對于圖像識別任務,卷積神經網絡的結構一般如下圖所示。輸入層讀入經過簡單的規則化(統一大小)的圖像。每一層中的單元將前一層中的一組小的局部近鄰的單元作為輸入。這種局部連接觀點來源于早期的感知器,并且和Hubel、Wiesel從貓科動物的視覺系統中發現的局部感知、方向選擇神經元相一致。通過局部感知場,神經元能夠抽取一些基本的視覺特征,比如有向邊、結束點、邊角等等。這些特征然后被更高層的神經元所使用。并且,適用于某個局部的基礎特征抽取器同樣也傾向于適用于整個圖像。通過利用這種特征,卷積神經網絡利用一組分布于圖像各個不同位置但具有相同權值向量的單元,來獲取圖像的特征并構成一幅特征圖(Feature Map)。在每個位置,來自不同特征圖的單元得到各自不同類型的特征。一個特征圖中的不同單元被限制為對輸入圖中的各個不同位置的局部數據進行同樣的操作。這種操作等同于將輸入圖像對于一個小的核進行卷積。一個卷積層中通常包含多個具有不同權值向量的特征圖,使得在同一個位置能夠獲得多種不同的特征。如下圖,第一個隱含層包含4個特征圖,每個特征圖由5*5的局部感知區域構成。一旦一個特征被檢測到,只要其相對于其他特征的相對位置沒有改變,那么其在圖像中的絕對位置就變得不是特別重要。因此,每個卷積層后面跟隨著一個降采樣層。降采樣層進行局部平均和降采樣的操作,降低特征圖的分辨率,同時降低了網絡輸出對于位移和變形的敏感程度。第二個隱含層進行2*2的平均化降采樣的操作。后續的卷積層和降采樣層都交替分布連接,構成一個“雙金字塔”結構:特征圖的數目逐漸增多,而且特征圖的分辨率逐漸降低。

由于所有權重都是通過反向傳播算法訓練得到 ,卷積神經網絡可以被看作自動合成其自身的特征抽取器。
一般情況下卷積神經網絡中,卷積層和降采樣層交替連接在一起,用于降低計算時間并逐步建立起更高的空間和數據結構不變性,并通過比較小的降采樣系數使得這些特性得以維持。
CNN的分類模型與傳統模型的不同點在于其可以直接將一幅二維圖像輸入模型中,接著在輸出端即給出分類結果。其優勢在于不需復雜的預處理,將特征抽取,模式分類完全放入一個黑匣子中,通過不斷的優化來獲得網絡所需參數,在輸出層給出所需分類,網絡核心就是網絡的結構設計與網絡的求解。這種求解結構比以往多種算法性能更高。
CNN是一個多層的神經網絡,每層由多個二維平面組成,而每個平面由多個獨立神經元組成。網絡中包含簡單元(S-元)和復雜元(C-元),S-元聚合在一起組成S-面,S-面聚合在一起組成S-層。C-元、C-面和C-層之間存在類似的關系。網絡的中間部分由S-層與C-層串接而成,輸入級只含一層,它直接接受二維視覺模式。樣本特征提取步驟已嵌入到卷積神經網絡模型的互聯結構中。
一般,S為特征提取層,每個神經元的輸入與前一層的局部感受野相連接,并提取該局部的特征,一旦該局部特征被提取,它與其它特征之間的位置關系就被確定;C是特征映射層,網絡的每個計算層由多個特征映射組成,每個特征映射為一個平面,平面上所有神經元的權值相同。特征映射結構采用影響函數核小的Sigmoid函數作為卷積網絡的激活函數,使得特征映射具有位移不變性。由于每個映射面上的神經元權值共享,減少了網絡的自由參數數目,降低了網絡參數選擇的復雜度。CNN中的每一個特征提取層(S-層)都跟著一個用來求局部平均與二次提取的計算層(C-層),這種特有的兩次特征提取結構使網絡在識別時對輸入樣本有較高的畸變容忍能力。
CNN網絡除了輸入輸出層,還有中間的卷積層,抽樣層與全連接層,將原始圖像直接輸入到輸入層,原始圖像的大小決定了輸入向量的尺寸,神經元提取圖像的局部特征,每個神經元都與前一層的局部感受野相連,通過交替出現的抽樣層(S)與卷積層(C)和最后的全連接層,在輸出層給出網絡的輸出。在卷積層和抽樣層中有若干個特征圖,每一層有多個平面,每層中各平面的神經元提取圖像中特定區域的局部特征,如邊緣特征,方向特征等,在訓練時不斷修正S-層神經元的權值。同一層面上的神經元權值相同,這樣可以有相同程度的位移、旋轉不變性。由于權值共享,所以從一個平面到下個平面的映射可以看做是作卷積運算,S-層可看作是模糊濾波器,起到二次特征提取的作用。隱層與隱層之間空間分辨率遞減,每層所含的平面數遞增,這樣可用于檢測更多的特征信息。
卷積層中,前一層的特征圖與一個可學習的核進行卷積,卷積的結果經過激活函數后的輸出形成這一層的神經元,從而構成該層特征圖。卷積層與抽樣層間隔出現,卷積層每一個輸出的特征圖可能與前一層的幾個特征圖的卷積建立關系。每個特征圖可以有不同的卷積核。卷積層主要的任務就是從不同的角度來選擇前一層特征圖的各角度特征使其具有位移不變性。卷積的本質就是對前一層的特征圖進行處理,來得到這一層的特征圖。抽樣層主要作用是降低網絡的空間分辨率,通過降低圖像的空間分辨率來消除偏移和圖像的扭曲。
隱層的參數個數和隱層的神經元個數無關,只和濾波器的大小和濾波器種類的多少有關。隱層的神經元個數,它和原圖像,也就是輸入的大小(神經元個數)、濾波器的大小和濾波器在圖像中的滑動步長都有關。
三、卷積神經網絡求解
CNN通過三個方法來實現識別圖像的位移、縮放和扭曲不變性,即局域感受野、權值共享和次抽樣。局域感受野指的是每一層網絡的神經元只與上一層的一個小鄰域內的神經單元連接,通過局域感受野,每個神經元可以提取初級的視覺特征,如方向線段,端點和角點等;權值共享使得CNN具有更少的參數,需要相對少的訓練數據;次抽樣可以減少特征的分辨率,實現對位移、縮放和其它形式扭曲的不變性。卷積層之后通常用一個次抽樣層來減少計算時間、建立空間和結構上的不變性。
構造好網絡之后,需要對網絡進行求解,如果像傳統神經網絡一樣分配參數,則每一個連接都會有未知參數。而CNN采用的是權值共享,這樣一來通過一幅特征圖上的神經元共享同樣的權值就可以大大減少自由參數,這可以用來檢測相同的特征在不同角度表示的效果。在網絡設計中通常都是抽樣層與卷積層交替出現,全連接層的前一層通常為卷積層。
在CNN中,權值更新是基于反向傳播算法。
CNN在本質上是一種輸入到輸出的映射,它能夠學習大量的輸入與輸出之間的映射關系,而不需要任何輸入和輸出之間的精確的數學表達式,只要用已知的模式對卷積網絡加以訓練,網絡就具有輸入輸出對之間的映射能力。卷積網絡執行的是監督訓練,所以其樣本集是由形如:輸入向量,理想輸出向量的向量對構成的。所有這些向量對,都應該是來源于網絡即將模擬系統的實際“運行”結構,它們可以是從實際運行系統中采集來。在開始訓練前,所有的權都應該用一些不同的隨機數進行初始化。“小隨機數”用來保證網絡不會因權值過大而進入飽和狀態,從而導致訓練失敗;“不同”用來保證網絡可以正常地學習。實際上,如果用相同的數去初始化權矩陣,則網絡無學習能力。
訓練算法主要包括四步,這四步被分為兩個階段:
第一階段,向前傳播階段:
(1)、從樣本集中取一個樣本,輸入網絡;
(2)、計算相應的實際輸出;在此階段,信息從輸入層經過逐級的變換,傳送到輸出層。這個過程也是網絡在完成訓練后正常執行時執行的過程。
第二階段,向后傳播階段:
(1)、計算實際輸出與相應的理想輸出的差;
(2)、按極小化誤差的方法調整權矩陣。
這兩個階段的工作一般應受到精度要求的控制。
網絡的訓練過程如下:
(1)、選定訓練組,從樣本集中分別隨機地尋求N個樣本作為訓練組;
(2)、將各權值、閾值,置成小的接近于0的隨機值,并初始化精度控制參數和學習率;
(3)、從訓練組中取一個輸入模式加到網絡,并給出它的目標輸出向量;
(4)、計算出中間層輸出向量,計算出網絡的實際輸出向量;
(5)、將輸出向量中的元素與目標向量中的元素進行比較,計算出輸出誤差;對于中間層的隱單元也需要計算出誤差;
(6)、依次計算出各權值的調整量和閾值的調整量;
(7)、調整權值和調整閾值;
(8)、當經歷M后,判斷指標是否滿足精度要求,如果不滿足,則返回(3),繼續迭代;如果滿足就進入下一步;
(9)、訓練結束,將權值和閾值保存在文件中。這時可以認為各個權值已經達到穩定,分類器已經形成。再一次進行訓練,直接從文件導出權值和閾值進行訓練,不需要進行初始化。
四、卷積神經網絡LeNet-5結構分析

CNN是一種帶有卷積結構的深度神經網絡,通常至少有兩個非線性可訓練的卷積層,兩個非線性的固定卷積層(又叫Pooling Layer或降采樣層)和一個全連接層,一共至少5個隱含層。
CNN的結構受到著名的Hubel-Wiesel生物視覺模型的啟發,尤其是模擬視覺皮層V1和V2層中Simple Cell和Complex Cell的行為。
LeNet-5手寫數字識別結構(上圖)分析:
1. 輸入層:N個32*32的訓練樣本
輸入圖像為32*32大小。這要比Mnist數據庫中最大的字母還大。這樣做的原因是希望潛在的明顯特征如筆畫斷點或角點能夠出現在最高層特征監測子感受野的中心。
2. C1層:
輸入圖片大小: 32*32
卷積窗大小: 5*5
卷積窗種類: 6
輸出特征圖數量: 6
輸出特征圖大小: 28*28 (32-5+1)
神經元數量: 4707 (28*28)*6)
連接數: 122304 (28*28*5*5*6)+(28*28*6)
可訓練參數: 156 5*5*6+6
用6個5×5的過濾器進行卷積,結果是在卷積層C1中,得到6張特征圖,特征圖的每個神經元與輸入圖片中的5×5的鄰域相連,即用5×5的卷積核去卷積輸入層,由卷積運算可得C1層輸出的特征圖大小為(32-5+1)×(32-5+1)=28×28。
3. S2層:
輸入圖片大小: (28*28)*6
卷積窗大小: 2*2
卷積窗種類: 6
輸出下采樣圖數量:6
輸出下采樣圖大小:14*14 (28/2)*(28/2)
神經元數量: 1176 (14*14)*6
連接數: 5880 2*2*14*14*6+14*14*6
可訓練參數: 12 1*6+6
卷積和子采樣過程:
(1)、卷積過程包括:用一個可訓練的濾波器fx去卷積一個輸入的圖像(第一階段是輸入的圖像,后面的階段就是卷積特征map了),然后加一個偏置bx,得到卷積層Cx。
卷積運算一個重要的特點就是,通過卷積運算,可以使原信號特征增強,并且降低噪音。
(2)、子采樣過程包括:每鄰域四個像素求和變為一個像素,然后通過標量Wx+1加權,再增加偏置bx+1,然后通過一個sigmoid激活函數,產生一個大概縮小四倍的特征映射圖Sx+1。
利用圖像局部相關性的原理,對圖像進行子抽樣,可以減少數據處理量同時保留有用信息。
卷積之后進行子抽樣的思想是受到動物視覺系統中的“簡單的”細胞后面跟著“復雜的”細胞的想法的啟發而產生的。
降采樣后,降采樣層S2的輸出特征圖大小為(28÷2)×(28÷2)=14×14。
S2層每個單元的4個輸入相加,乘以一個可訓練參數,再加上一個可訓練偏置。結果通過sigmoid函數計算。可訓練系數和偏置控制著sigmoid函數的非線性程度。如果系數比較小,那么運算近似于線性運算,下采樣相當于模糊圖像。如果系數比較大,根據偏置的大小下采樣可以被看成是有噪聲的“或”運算或者有噪聲的“與”運算。每個單元的2*2感受野并不重疊,因此S2中每個特征圖的大小是C1中特征圖大小的1/4(行和列各1/2)。
從一個平面到下一個平面的映射可以看作是作卷積運算,S-層可看作是模糊濾波器,起到二次特征提取的作用。隱層與隱層之間空間分辨率遞減,而每層所含的平面數遞增,這樣可用于檢測更多的特征信息。
4. C3層:
輸入圖片大小: (14*14)*6
卷積窗大小: 5*5
卷積窗種類: 16
輸出特征圖數量: 16
輸出特征圖大小: 10*10 (14-5+1)
神經元數量: 1600 (10*10)*16)
連接數: 151600 1516*10*10
可訓練參數: 1516 6*(3*25+1)+6*(4*25+1)+3*(4*25+1)+1*(6*25+1)
C3層也是一個卷積層,它同樣通過5x5的卷積核去卷積S2層,然后得到的特征map就只有10x10個神經元,但是它有16種不同的卷積核,所以就存在16個特征map了。這里需要注意的一點是:C3中的每個特征map是連接到S2中的所有6個或者幾個特征map的,表示本層的特征map是上一層提取到的特征map的不同組合(這個做法也并不是唯一的)。
C3中每個特征圖由S2中所有6個或者幾個特征map組合而成。為什么不把S2中的每個特征圖連接到每個C3的特征圖呢?原因有2點。第一,不完全的連接機制將連接的數量保持在合理的范圍內。第二,也是最重要的,其破壞了網絡的對稱性。由于不同的特征圖有不同的輸入,所以迫使他們抽取不同的特征。
5. S4層:
輸入圖片大小: (10*10)*16
卷積窗大小: 2*2
卷積窗種類: 16
輸出下采樣圖數量: 16
輸出下采樣圖大小: (5*5)*16
神經元數量: 400 (5*5)*16
連接數: 2000 (2*2*5*5*16)+(5*5*16)
可訓練參數: 32 (1+1)*16
S4層是一個下采樣層,由16個5*5大小的特征圖構成。特征圖中的每個單元與C3中相應特征圖的2*2鄰域相連接,跟C1和S2之間的連接一樣。S4層有32個可訓練參數(每個特征圖1個因子和一個偏置)和2000個連接。
6. C5層:
輸入圖片大小: (5*5)*16
卷積窗大小: 5*5
卷積窗種類: 120
輸出特征圖數量: 120
輸出特征圖大小: 1*1 (5-5+1)
神經元數量: 120 (1*120)
連接數: 48120 5*5*16*120*1+120*1
可訓練參數: 48120 5*5*16*120+120
C5層是一個卷積層,有120個特征圖。每個單元與S4層的全部16個單元的5*5鄰域相連。由于S4層特征圖的大小也為5*5(同濾波器一樣),故C5特征圖的大小為1*1,這構成了S4和C5之間的全連接。之所以仍將C5標示為卷積層而非全相聯層,是因為如果LeNet-5的輸入變大,而其他的保持不變,那么此時特征圖的維數就會比1*1大。C5層有48120個可訓練連接。
7. F6層:
輸入圖片大小: (1*1)*120
卷積窗大小: 1*1
卷積窗種類: 84
輸出特征圖數量: 1
輸出特征圖大小: 84
神經元數量: 84
連接數: 10164 120*84+84
可訓練參數: 10164 120*84+84
F6層有84個單元(之所以選這個數字的原因來自于輸出層的設計),與C5層全相連。有10164個可訓練參數。如同經典神經網絡,F6層計算輸入向量和權重向量之間的點積,再加上一個偏置。然后將其傳遞給sigmoid函數產生單元i的一個狀態。
8. OUTPUT層:
輸入圖片大小: 1*84
輸出特征圖數量: 1*10
最后,輸出層由歐式徑向基函數(EuclideanRadial Basis Function)單元組成,每類一個單元,每個有84個輸入。換句話說,每個輸出RBF單元計算輸入向量和參數向量之間的歐式距離。輸入離參數向量越遠,RBF輸出的越大。一個RBF輸出可以被理解為衡量輸入模式和與RBF相關聯類的一個模型的匹配程度的懲罰項。用概率術語來說,RBF輸出可以被理解為F6層配置空間的高斯分布的負log-likelihood。給定一個輸入模式,損失函數應能使得F6的配置與RBF參數向量(即模式的期望分類)足夠接近。這些單元的參數是人工選取并保持固定的(至少初始時候如此)。這些參數向量的成分被設為-1或1。雖然這些參數可以以-1和1等概率的方式任選,或者構成一個糾錯碼,但是被設計成一個相應字符類的7*12大小(即84)的格式化圖片。這種表示對識別單獨的數字不是很有用,但是對識別可打印ASCII集中的字符串很有用。
使用這種分布編碼而非更常用的“1 of N”編碼用于產生輸出的另一個原因是,當類別比較大的時候,非分布編碼的效果比較差。原因是大多數時間非分布編碼的輸出必須為0。這使得用sigmoid單元很難實現。另一個原因是分類器不僅用于識別字母,也用于拒絕非字母。使用分布編碼的RBF更適合該目標。因為與sigmoid不同,他們在輸入空間的較好限制的區域內興奮,而非典型模式更容易落到外邊。
RBF參數向量起著F6層目標向量的角色。需要指出這些向量的成分是+1或-1,這正好在F6 sigmoid的范圍內,因此可以防止sigmoid函數飽和。實際上,+1和-1是sigmoid函數的最大彎曲的點處。這使得F6單元運行在最大非線性范圍內。必須避免sigmoid函數的飽和,因為這將會導致損失函數較慢的收斂和病態問題。
五、卷積神經網絡注意事項
1. 數據集的大小和分塊
數據驅動的模型一般依賴于數據集的大小,CNN和其它經驗模型一樣,能適用于任意大小的數據集,但用于訓練的數據集應該足夠大,能夠覆蓋問題域中所有已知可能出現的問題。設計CNN的時候,數據集中應該包含三個子集:訓練集、測試集、驗證集。訓練集應該包含問題域中的所有數據,并在訓練階段用來調整網絡權值。測試集用來在訓練過程中測試網絡對于訓練集中未出現的數據的分類性能。根據網絡在測試集上的性能情況,網絡的結構可能需要做出調整,或者增加訓練循環的次數。驗證集中的數據同樣應該包含在測試集合訓練集中沒有出現過的數據,用于在確定網絡結構后能夠更加好的測試和衡量網絡的性能。Looney等人建議,數據集中的65%用于訓練,25%用于測試,剩余的10%用于驗證。
2. 數據預處理
為了加速訓練算法的收斂速度,一般都會采用一些數據預處理技術,這其中包括:去除噪聲、輸入數據降維、刪除無關數據等。數據的平衡化在分類問題中異常重要,一般認為訓練集中的數據應該相對于標簽類別近似于平均分布,也就是每一個類別標簽所對應的數據量在訓練集中是基本相等的,以避免網絡過于傾向于表現某些分類的特點。為了平衡數據集,應該移除一些過度富余的分類中的數據,并相應的補充一些相對樣例稀少的分類中的數據。還有一個辦法就是復制一部分這些樣例稀少分類中的數據,并在這些輸入數據中加入隨機噪聲。
3. 數據規則化
將數據規則化到一個統一的區間(如[0,1])中具有很重要的優點:防止數據中存在較大數值的數據造成數值較小的數據對于訓練效果減弱甚至無效化。一個常用的方法是將輸入和輸出數據按比例調整到一個和激活函數(sigmoid函數等)相對應的區間。
4. 網絡權值初始化
CNN的初始化主要是初始化卷積層和輸出層的卷積核(權重)和偏置。
網絡權值初始化就是將網絡中的所有連接權值(包括閾值)賦予一個初始值。如果初始權值向量處在誤差曲面的一個相對平緩的區域的時候,網絡訓練的收斂速度可能會異常緩慢。一般情況下,網絡的連接權值和閾值被初始化在一個具有0均值的相對小的區間內均勻分布,比如[-0.30, +0.30]這樣的區間內。
5. BP算法的學習速率
如果學習速率n選取的比較大則會在訓練過程中較大幅度的調整權值w,從而加快網絡訓練的速度,但這會造成網絡在誤差曲面上搜索過程中頻繁抖動且有可能使得訓練過程不能收斂,而且可能越過一些接近優化w。同樣,比較小的學習速率能夠穩定的使得網絡逼近于全局最優點,但也有可能陷入一些局部最優區域。對于不同的學習速率設定都有各自的優缺點,而且還有一種自適應的學習速率方法,即n隨著訓練算法的運行過程而自行調整。
6. 收斂條件
有幾個條件可以作為停止訓練的判定條件,訓練誤差、誤差梯度和交叉驗證。一般來說,訓練集的誤差會隨著網絡訓練的進行而逐步降低。
7. 訓練方式
訓練樣例可以有兩種基本的方式提供給網絡訓練使用,也可以是兩者的結合:逐個樣例訓練(EET)、批量樣例訓練(BT)。在EET中,先將第一個樣例提供給網絡,然后開始應用BP算法訓練網絡,直到訓練誤差降低到一個可以接受的范圍,或者進行了指定步驟的訓練次數。然后再將第二個樣例提供給網絡訓練。EET的優點是相對于BT只需要很少的存儲空間,并且有更好的隨機搜索能力,防止訓練過程陷入局部最小區域。EET的缺點是如果網絡接收到的第一個樣例就是劣質(有可能是噪音數據或者特征不明顯)的數據,可能使得網絡訓練過程朝著全局誤差最小化的反方向進行搜索。相對的,BT方法是在所有訓練樣例都經過網絡傳播后才更新一次權值,因此每一次學習周期就包含了所有的訓練樣例數據。BT方法的缺點也很明顯,需要大量的存儲空間,而且相比EET更容易陷入局部最小區域。而隨機訓練(ST)則是相對于EET和BT一種折衷的方法,ST和EET一樣也是一次只接受一個訓練樣例,但只進行一次BP算法并更新權值,然后接受下一個樣例重復同樣的步驟計算并更新權值,并且在接受訓練集最后一個樣例后,重新回到第一個樣例進行計算。ST和EET相比,保留了隨機搜索的能力,同時又避免了訓練樣例中最開始幾個樣例如果出現劣質數據對訓練過程的過度不良影響。
以上整理的內容主要摘自:
1. 《Gradient-Based Learning Applied to Document Recognition》,1998,Yann LeCun
2. 《卷積神經網絡在圖像識別上的應用研究》,2012,碩論,浙江大學
3. 《卷積神經網絡的研究與應用》,2013,碩論,南京林業大學
4. 《卷積神經網絡及其應用》,2014,碩論,大連理工大學
5. 《基于卷積神經網絡的深度學習算法與應用研究》,2014,碩論,浙江工商大學
 電子發燒友App
電子發燒友App





















評論