上一次我們用了單隱層的神經網絡,效果還可以改善,這一次就使用CNN。
卷積神經網絡

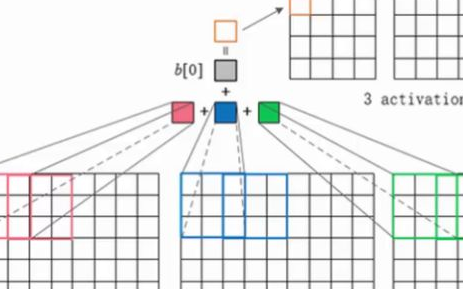
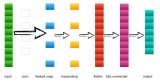
上圖演示了卷積操作
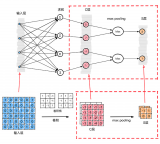
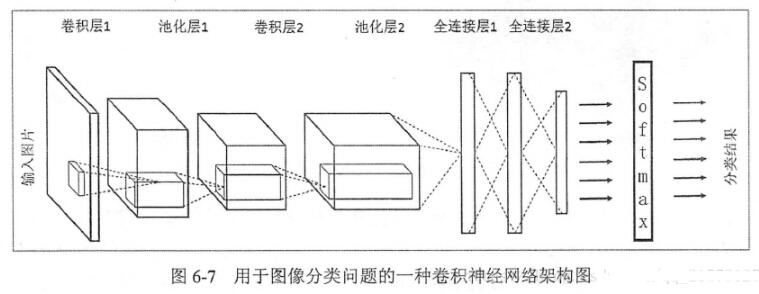
LeNet-5式的卷積神經網絡,是計算機視覺領域近期取得的巨大突破的核心。卷積層和之前的全連接層不同,采用了一些技巧來避免過多的參數個數,但保持了模型的描述能力。這些技巧是:
1, 局部聯結:神經元僅僅聯結前一層神經元的一小部分。
2, 權重共享:在卷積層,神經元子集之間的權重是共享的。(這些神經元的形式被稱為特征圖[feature map])
3, 池化:對輸入進行靜態的子采樣。
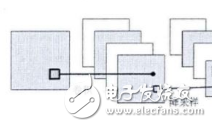
局部性和權重共享的圖示
卷積層的單元實際上連接了前一層神經元中的一個2維patch,這個前提讓網絡利用了輸入中的2維結構。
當使用Lasagne中的卷積層時,我們必須進行一些輸入準備。輸入不再像剛剛一樣是一個9216像素強度的扁平向量,而是一個有著(c,0,1)形式的三維矩陣,其中c代表通道(顏色),0和1對應著圖像的x和y維度。在我們的問題中,具體的三維矩陣為(1,96,96),因為我們僅僅使用了灰度一個顏色通道。
一個函數load2d對前述的load函數進行了包裝,完成這個2維到三維的轉變:
def load2d(test=False, cols=None):
X, y = load(test=test)
X = X.reshape(-1, 1, 96, 96)
return X, y
我們將要創建一個具有三個卷積層和兩個全連接層的卷積神經網絡。每個卷積層都跟著一個2*2的最大化池化層。初始卷積層有32個filter,之后每個卷積層我們把filter的數量翻番。全連接的隱層包含500個神經元。
這里還是一樣沒有任何形式(懲罰權重或者dropout)的正則化。事實證明當我們使用尺寸非常小的filter,如3*3或2*2,已經起到了非常不錯的正則化效果。
代碼如下:
net2 = NeuralNet(
layers=[
('input', layers.InputLayer),
('conv1', layers.Conv2DLayer),
('pool1', layers.MaxPool2DLayer),
('conv2', layers.Conv2DLayer),
('pool2', layers.MaxPool2DLayer),
('conv3', layers.Conv2DLayer),
('pool3', layers.MaxPool2DLayer),
('hidden4', layers.DenseLayer),
('hidden5', layers.DenseLayer),
('output', layers.DenseLayer),
],
input_shape=(None, 1, 96, 96),
conv1_num_filters=32, conv1_filter_size=(3, 3), pool1_pool_size=(2, 2),
conv2_num_filters=64, conv2_filter_size=(2, 2), pool2_pool_size=(2, 2),
conv3_num_filters=128, conv3_filter_size=(2, 2), pool3_pool_size=(2, 2),
hidden4_num_units=500, hidden5_num_units=500,
output_num_units=30, output_nonlinearity=None,
update_learning_rate=0.01,
update_momentum=0.9,
regression=True,
max_epochs=1000,
verbose=1,
)
X, y = load2d() # load 2-d data
net2.fit(X, y)
# Training for 1000 epochs will take a while. We'll pickle the
# trained model so that we can load it back later:
import cPickle as pickle
with open('net2.pickle', 'wb') as f:
pickle.dump(net2, f, -1)
訓練這個網絡和第一個網絡相比,將要耗費巨大的時空資源。每次迭代要慢15倍,整個1000次迭代下來要耗費20多分鐘的時間,這還是在你有一個相當不錯的GPU的基礎上。
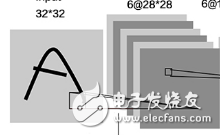
然而耐心總是得到回饋,我們的模型和結果自然比剛剛好得多。讓我們來看一看運行腳本時的輸出。首先是輸出形狀的層列表,注意因為我們選擇的窗口尺寸,第一個卷積層的32個filter輸出了32張94*94 的特征圖。
InputLayer (None, 1, 96, 96) produces 9216 outputs
Conv2DCCLayer (None, 32, 94, 94) produces 282752 outputs
MaxPool2DCCLayer (None, 32, 47, 47) produces 70688 outputs
Conv2DCCLayer (None, 64, 46, 46) produces 135424 outputs
MaxPool2DCCLayer (None, 64, 23, 23) produces 33856 outputs
Conv2DCCLayer (None, 128, 22, 22) produces 61952 outputs
MaxPool2DCCLayer (None, 128, 11, 11) produces 15488 outputs
DenseLayer (None, 500) produces 500 outputs
DenseLayer (None, 500) produces 500 outputs
DenseLayer (None, 30) produces 30 outputs
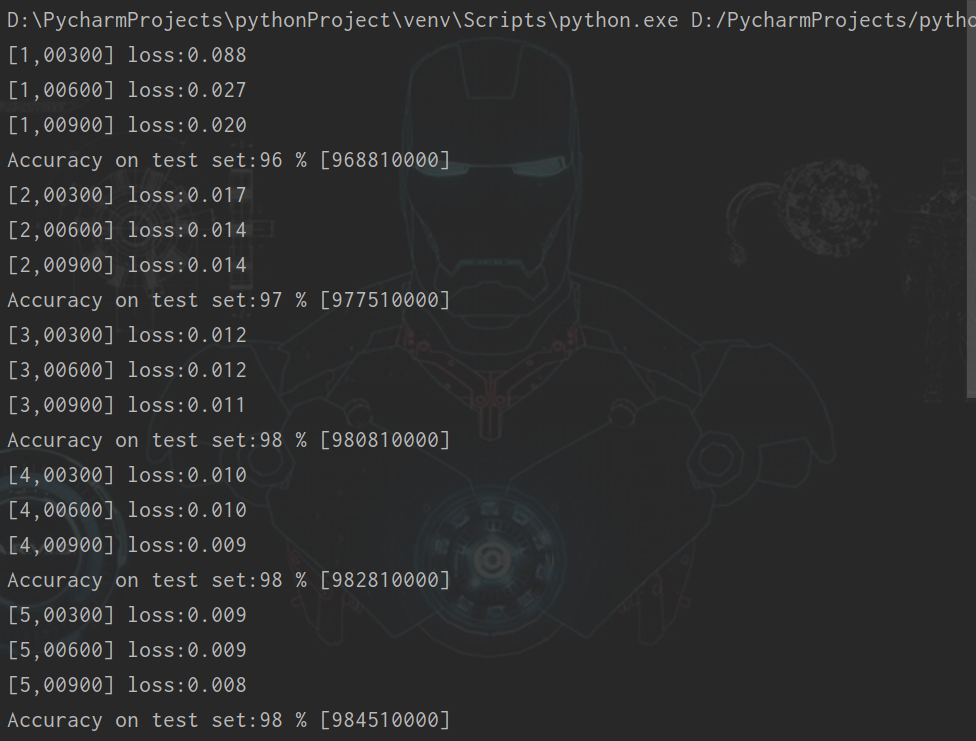
接下來我們看到,和第一個網絡輸出相同,是每一次迭代訓練損失和驗證損失以及他們之間的比率。
Epoch | Train loss | Valid loss | Train / Val
--------|--------------|--------------|----------------
1 | 0.111763 | 0.042740 | 2.614934
2 | 0.018500 | 0.009413 | 1.965295
3 | 0.008598 | 0.007918 | 1.085823
4 | 0.007292 | 0.007284 | 1.001139
5 | 0.006783 | 0.006841 | 0.991525
...
500 | 0.001791 | 0.002013 | 0.889810
501 | 0.001789 | 0.002011 | 0.889433
502 | 0.001786 | 0.002009 | 0.889044
503 | 0.001783 | 0.002007 | 0.888534
504 | 0.001780 | 0.002004 | 0.888095
505 | 0.001777 | 0.002002 | 0.887699
...
995 | 0.001083 | 0.001568 | 0.690497
996 | 0.001082 | 0.001567 | 0.690216
997 | 0.001081 | 0.001567 | 0.689867
998 | 0.001080 | 0.001567 | 0.689595
999 | 0.001080 | 0.001567 | 0.689089
1000 | 0.001079 | 0.001566 | 0.688874
1000次迭代后的結果相對第一個網絡,有了非常不錯的改善,我們的RMSE也有不錯的結果。
>>> np.sqrt(0.001566) * 48
1.8994904579913006
 電子發燒友App
電子發燒友App




















評論