1.概述
SVPWM是近年發展的一種比較新穎的控制方法,是由三相功率逆變器的六個功率開關元件組成的特定開關模式產生的脈寬調制波,能夠使輸出電流波形盡可能接近于理想的正弦波形。空間電壓矢量PWM與傳統的正弦PWM不同,它是從三相輸出電壓的整體效果出發,著眼于如何使電機獲得理想圓形磁鏈軌跡。SVPWM技術與SPWM相比較,繞組電流波形的諧波成分小,使得電機轉矩脈動降低,旋轉磁場更逼近圓形,而且使直流母線電壓的利用率有了很大提高,且更易于實現數字化。
2.SVPWM基本原理
SVPWM 的理論基礎是平均值等效原理,即在一個開關周期內通過對基本電壓矢量加以組合,使其平均值與給定電壓矢量相等。
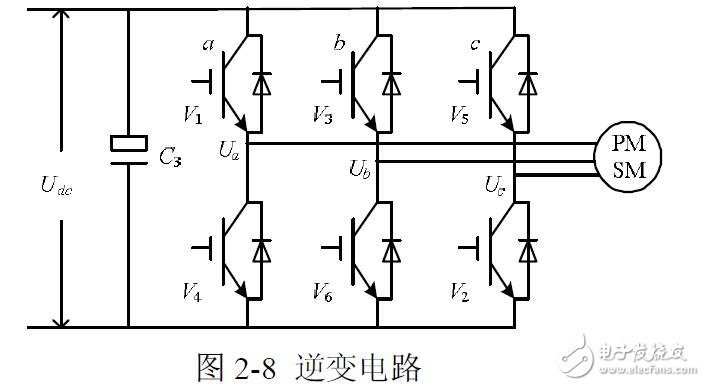
在上圖的逆變電路中,設直流母線上的電壓為Udc,逆變器輸出的三相相電壓為UA、UB、UC,其分別施加在空間上互差120度的平面坐標系上,定義這三個電壓空間矢量為UA(t)、UB(t)、UC(t),他們方向始終在各自的軸線上,而大小隨時間按正弦規律變化,時間相位上互差120度。假設Um為相電壓的有效值,f為電源頻率,則有:

可見U(t)是一個旋轉的空間矢量,它的幅值不變,為相電壓峰值,且以角頻率ω= 2πf按逆時針方向勻速旋轉的空間矢量。而SVPWM算法的目的就是使用三相橋的開關狀態把在空間中旋轉的U(t)矢量表示出來。
由于逆變器三相橋臂共有6個開關管,為了研究各相上下橋臂不同開關組合 時逆變器輸出的空間電壓矢量,特定義開關函數Sx(x=a、b、c) 為:

(Sa、Sb、Sc)的全部可能組合共有八個,包括 6個非零矢量Ul(001)、U2(010)、U3(011)、U4(100)、U5(101)、U6(110)、和兩個零矢量 U0(000)、U7(111),下面以其中一種開關組合為例分析,假設Sx(x=a、b、c)=(100),此時等效電路如圖:
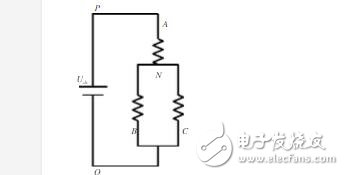
因此相電壓可以表示為:(相電壓是每相相對于電機中間連接點的電壓)
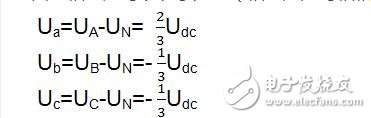
同理可得,其他開關狀態三相的相電壓。另外線電壓是兩相之間的電壓差,如Uab=Ua-Ub。如前面所說
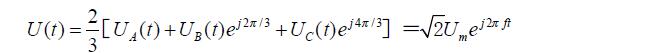
當開關Sa=1時,UA(t)=Udc;當開關Sb=1時,UB(t)=Udc;當開關Sc=1時,UC(t)=Udc。因此上式可以寫成:
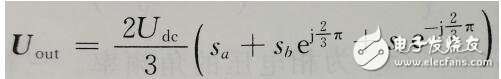
可以看到Uout的模值不變,改變的只是相位。
開關狀態與線電壓、相電壓、Uout列在一起:
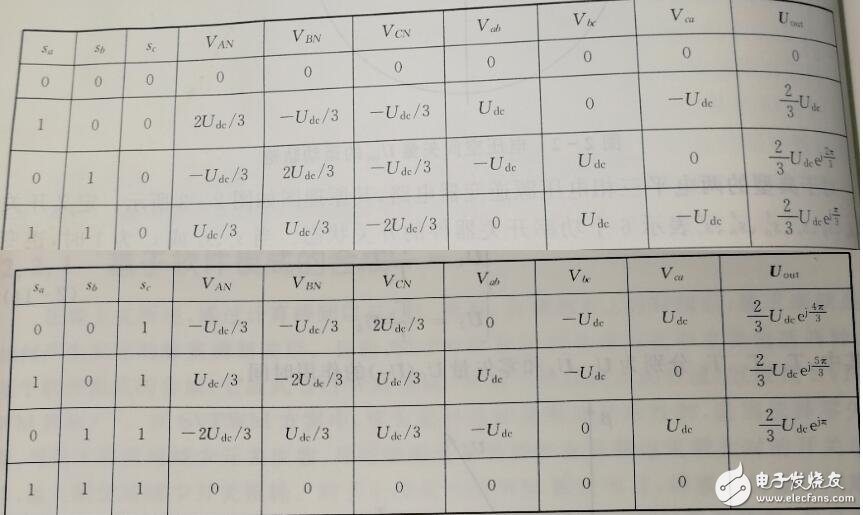
把上面的8個電壓空間矢量按照Uout的相位關系放在扇區圖中:

上圖中,6個非零矢量幅值相同,相鄰的矢量間隔60度。兩個零矢量幅值為零,位于中心。
三相電壓給定所合成的電壓向量旋轉角速度為ω=2πf,則旋轉一周所需的時間為T=1/ f;若載波頻率是 fs ,則頻率比為 R=fs / f。這樣將電壓旋轉平面等切割成R個小增量,亦即設定電壓向量每次增量的角度是:γ=2π/ R。
現在假設需要輸出一個空間矢量Uref,假設它在第I扇區,我們先把第I扇區單獨取出來,然后用和它相鄰的兩個電壓空間矢量來表示它:
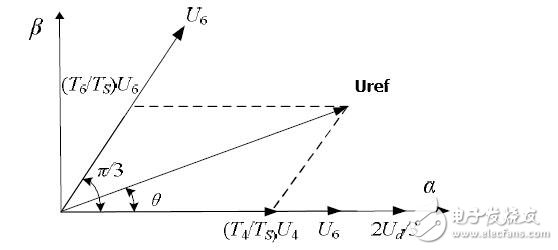

得到以 U4、U6、U7 及 U0 合成的 Uref 的時間后,接下來就是如何產生實際的脈寬調制波形。在 SVPWM 調制方案中,零矢量的選擇是最具靈活性的,適當選擇零矢量,可最大限度地減少開關次數,盡可能避免在負載電流較大的時刻的開關動作,最大限度地減少開關損耗。因此,我們以減少開關次數為目標,將基本矢量作用順序的分配原則選定為:在每次開關狀態轉換時,只改變其中一相的開關狀態。并且對零矢量在時間上進行了平均分配,以使產生的 PWM 對稱,從而有效地降低 PWM 的諧波分量。可以發現當 U4(100)切換至 U0(000)時,只需改變 A 相上下一對切換開關,若由 U4(100)切換至 U7(111)則需改變 B、C 相上下兩對切換開關,增加了一倍的切換損失。因此要改變電壓向量 U4(100)、U2(010)、U1(001)的大小,需配合零電壓向量 U0(000),而要改變 U6(110)、U3(011)、U5(100), 需配合零電壓向量 U7(111)。這樣通過在不同區間內安排不同的開關切換順序, 就可以獲得對稱的輸出波形,其它各扇區的開關切換順序如表 2-2 所示。

因此就可以利用 U4、U6、U7 及 U0 的順序和時間長短的搭配來表示出Uref了。
以第Ⅰ扇區為例,其所產生的三相波調制波形在一個載波周期時間Ts 內如圖 2-11 所示,圖中電壓向量出現的先后順序為 U0、U4、U6、U7、U6、U4、U0,各電壓向量的三相波形則與表 2-2 中的開關表示符號相對應。再下一個 載波周期Ts ,Uref 的角度增加一個γ,利用式(2-33)可以重新計算新的 T0、T4、T6 及 T7 值,得到新的類似圖 2-11 的合成三相波形;這樣每一個載波周期 TS 就會合成一個新的矢量,隨著 θ 的逐漸增大,Uref 將依序進入第Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ、Ⅵ區。在電壓向量旋轉一周期后,就會產生 R 個合成矢量。
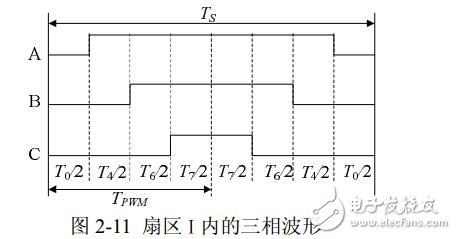
因此SVPWM會在每個載波周期進行一次計算。
通過以上 SVPWM 的法則推導分析可知要實現 SVPWM 信號的實時調制, 首先需要知道參考電壓矢量 Uref 所在的區間位置,然后利用所在扇區的相鄰兩電壓矢量和適當的零矢量來合成參考電壓矢量。
控制系統需要輸出的矢量電壓信號 Uref,它以某一角頻率 ω 在空間逆時針旋轉,當旋轉到矢量圖的某個 60°扇區中時,系統計算該區間所需的基本電壓空間矢量,并以此矢量所對應的狀態去驅動功率開關元件動作。當控制矢量在空間旋轉 360°后,逆變器就能輸出一個周期的正弦波電壓。
1.合成矢量Uref 所處扇區N 的判斷
空間矢量調制的第一步是判斷由Uα 和Uβ所決定的空間電壓矢量所處的扇區。
假定合成的電壓矢量落在第 I 扇區,可知其等價條件如下: 0《arctan(Uβ/ Uα) 《60
落在第 I 扇區的充分必要條件為:Ua 》 0 ,Uβ 》 0 且Uβ/Ua 《√3。
同理可得到合成的電壓矢量落在其它扇區的等價條件,得出:
Uref落在第Ⅱ扇區的充要條件為:Ua》0 且Uβ/ Ua》√3;
Uref落在第Ⅲ扇區的充要條件為:Ua《0 ,Uβ》 0 且-Uβ/Ua 《√3;
Uref落在第Ⅳ扇區的充要條件為:Ua《0 ,Uβ 《 0 且Uβ/Ua 《√3;
Uref落在第Ⅴ扇區的充要條件為:Uβ《0 且 -Uβ/Ua》√3;
Uref落在第Ⅵ扇區的充要條件為:Ua》0 ,Uβ《0且-Uβ/Ua 《√3;
若進一步分析以上的條件,可看出參考電壓矢量 Uref 所在的扇區完全由Uβ、√3Ua-Uβ、-√3Ua-Uβ三式決定,因此令:

再定義,若U1 》 0 ,則 A=1,否則 A=0;
若U2 》 0 ,則B=1,否則 B=0;
若U3 》 0 ,則 C=1,否則 C=0。
可以看出 A,B,C 之間共有八種組合,但由判斷扇區的公式可知 A,B,C 不會同時為 1 或同時為 0,所以實際的組合是六種,A,B,C 組合取不同的值對應著不同的扇區,并且是一一對應的,因此完全可以由 A,B,C 的組合判斷所在的扇區。為區別六種狀態,令 N=4*C+2*B+A,則可以通過下表計算參考電壓矢量Uref所在的扇區。

采用上述方法,只需經過簡單的加減及邏輯運算即可確定所在的扇區,對于提高系統的響應速度和進行仿真都是很有意義的。
2.基本矢量作用時間計算與三相 PWM 波形的合成
在傳統 SVPWM 算法如式(2-34)中用到了空間角度及三角函數,使得直接計算基本電壓矢量作用時間變得十分困難。實際上,只要充分利用 Uα 和 Uβ 就可以使計算大為簡化。
以Uref 處在第Ⅰ扇區時進行分析,根據圖 2-10 有:

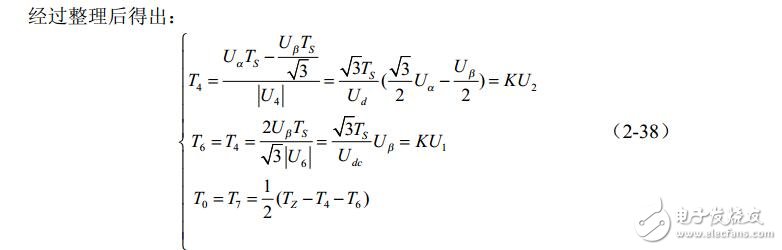
同理可求得Uref在其它扇區中各矢量的作用時間,結果如表2-4所示。表中兩個非零矢量作用時間的比例系數為 K =3Ts/Udc 。由此可根據式2-36 中的U1 、U2、U3判斷合成矢量所在扇區,然后查表得出兩非零矢量的作用時間,最后得出三相PWM波占空比,表2-4可以使SVPWM算法編程簡易實現。
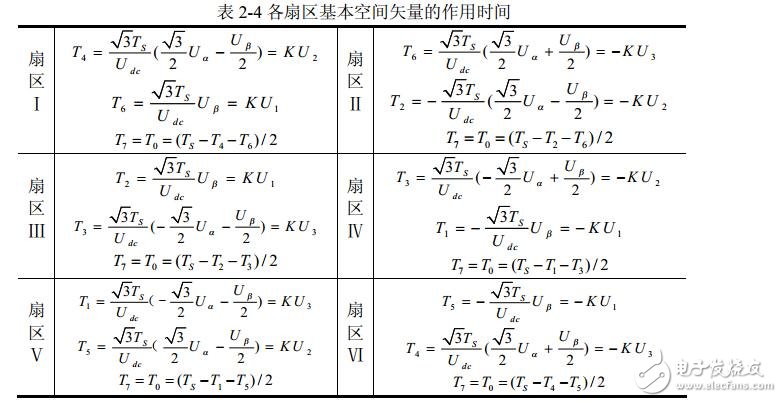
由公式(2-38)可知,當兩個零電壓矢量作用時間為0時,一個PWM周期內非零電壓矢量的作用時間最長,此時的合成空間電壓矢量幅值最大,由下圖2-12可知其幅值最大不會超過圖中所示的正六邊形邊界。而當合成矢量落在該邊界之外時,將發生過調制,逆變器輸出電壓波形將發生失真。在SVPWM調制模式下,逆變器能夠輸出的最大不失真圓形旋轉電壓矢量為圖2-12所示虛線正六邊形的內切圓,其幅值為: (√3/ 2)x(2Udc / 3) =√3Udc /3 。即逆變器輸出的不失真最大正弦相電壓幅值為√3Udc /3 ,而若采用三相SPWM調制,逆變器能輸出的不失真 最大正弦相電壓幅值為Udc/2。顯然SVPWM 調制模式下對直流側電壓利用率更高,它們的直流利用率之比為(√3Udc / 3) /(Udc / 2) =1.1547 ,即SVPWM算法比SPWM算法的直流電壓利用率提高了15.47%。
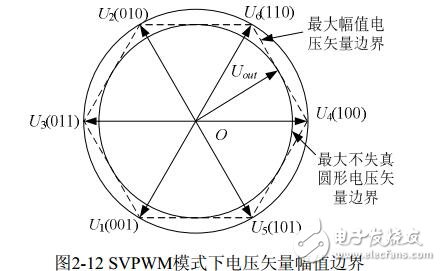
如圖當合成電壓矢量端點落在正六邊形與外接圓之間時,已發生過調制,輸出電壓將發生失真,必須采取過調制處理,這里采用一種比例縮小算法。定義每個扇區中先發生的矢量用為 Tx,后發生的矢量為 Ty。當 Tx+Ty≤TS時,矢量端點在正六邊形之內,不發生過調制;當 Tx+Ty》TS時,矢量端點超出正六邊形,發生過調制。輸出的波形會出現嚴重的失真,需采取以下措施:
設將電壓矢量端點軌跡端點拉回至正六邊形內切圓內時兩非零矢量作用時間分別為 Tx‘,Ty’,則有比例關系:

 電子發燒友App
電子發燒友App












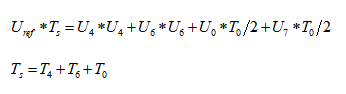










評論