描述

數學很難。當你的老師不喜歡教它時。

根據維基百科，

CUDA （Compute Unified Device Architecture）是由Nvidia創建的并行計算平臺和應用程序編程接口（API）模型。它允許軟件開發人員和軟件工程師使用支持 CUDA 的圖形處理單元 (GPU) 進行通用處理——一種稱為 GPGPU（圖形處理單元上的通用計算）的方法。CUDA平臺是一個軟件層，可直接訪問 GPU 的虛擬指令集和并行計算元素，以執行計算內核。

CUDA （Compute Unified Device Architecture）是由Nvidia創建的并行計算平臺和應用程序編程接口（API）模型。它允許軟件開發人員和軟件工程師使用支持 CUDA 的圖形處理單元 (GPU) 進行通用處理——一種稱為 GPGPU（圖形處理單元上的通用計算）的方法。CUDA平臺是一個軟件層，可直接訪問 GPU 的虛擬指令集和并行計算元素，以執行計算內核。

換句話說，英偉達提供了一個新的開發框架，由硬件和軟件組成，用于并行計算任務，從而減少完成時間。

CUDA 范例由具有多個處理器的專用硬件和 C/C++ 語言的巧妙擴展組成，能夠通過簡單的任務來處理每個處理器的功能。當您必須執行搜索、查詢、排序和卷積等重復性任務時，您可以（部分）擺脫繁重的循環，并將一小部分操作安排給不同的工作人員。由于數千個工作線程并行運行，完成任務的時間大大減少。

當然也有一些注意事項：雖然串行馮諾依曼調度只需要一個輸入、一個在指令后完成詳細說明的黑盒和一個輸出，但并行架構需要考慮數據存儲在哪里，誰在處理它（以及如何），一些數據何時可以免費用于下一次評估。并發分析并不容易，但是一旦你知道了基礎，它就變得簡單了。

CUDA 硬件 – Jetson Nano

CUDA 迎來了它的第 10 個化身，展示了作為一個強大而穩定的開發工具。CUDA 作為一種圖形架構誕生，能夠在顯示器上快速處理像素并驅動其顏色，如今已成為一個完整的并行開發系統。雖然它的名氣仍然存在于圖形數據處理和成像領域，但越來越多的開發人員投入時間和精力來揭示和利用隱藏在裸機中的并行能力。工程師和數學研究人員重構了眾所周知的串行算法，以利用多處理的驚人速度。

沒錯。我們開發了一種帶有 CUDA GPU 的并行分解算法，比原始 CPU 方法快 1,000 倍。只需將一個線程專用于 960 個殘差類（共 4620 個）中的每一個，我們就有了如此巨大的加速。但是Jetson Nano沒有 960 個備用計算單元，雖然它仍然可以從 128 個 CUDA 內核中受益，但我們將在其上測試不同的分解算法。

我們將嘗試一種完全不同的方法，而不是使用 125 cu 將工作細分為 8 個塊，但確定性稍差，但這將利用Jetson Nano使用統計模擬的有限 CUDA。

?

分解——Pollard Rho 算法

來自維基百科：

假設我們需要分解一個數 n = p*q，其中 p 是一個非平凡的因子。一個多項式模 n，稱為 g(x)（例如，g(x) = (x2 + 1) mod n，用于生成偽隨機序列。選擇一個起始值，比如 2，序列繼續為 x1 =g(2), x2=g(g(2)), x3=g(g(g(2))) 等。該序列與另一個序列{xk mod p}有關。由于事先不知道p ，這個序列在算法中是無法明確計算的，但算法的核心思想就在其中。

因為這些序列的可能值的數量是有限的（模運算保證了它），所以 {xk} 序列（即 mod n）和 {xk mod p} 序列最終都會重復，即使我們不知道后者. 假設序列表現得像隨機數。由于生日悖論（我們將在另一篇文章中分析），重復發生之前的 xk 的數量預計為 O(√N)，其中 N 是可能值的數量。所以序列 {xk mod p} 可能會比序列 {xk} 更早地重復。一旦一個序列有一個重復的值，這個序列就會循環，因為每個值只依賴于它之前的值。這種最終循環的結構產生了“Rho 算法”的名稱，因為當值 x1 mod p、x2 mod p 等時，它與希臘字符 ρ 的形狀相似。

假設我們需要分解一個數 n = p*q，其中 p 是一個非平凡的因子。一個多項式模 n，稱為 g(x)（例如，g(x) = (x2 + 1) mod n，用于生成偽隨機序列。選擇一個起始值，比如 2，序列繼續為 x1 =g(2), x2=g(g(2)), x3=g(g(g(2))) 等。該序列與另一個序列{xk mod p}有關。由于事先不知道p ，這個序列在算法中是無法明確計算的，但算法的核心思想就在其中。
因為這些序列的可能值的數量是有限的（模運算保證了它），所以 {xk} 序列（即 mod n）和 {xk mod p} 序列最終都會重復，即使我們不知道后者. 假設序列表現得像隨機數。由于生日悖論（我們將在另一篇文章中分析），重復發生之前的 xk 的數量預計為 O(√N)，其中 N 是可能值的數量。所以序列 {xk mod p} 可能會比序列 {xk} 更早地重復。一旦一個序列有一個重復的值，這個序列就會循環，因為每個值只依賴于它之前的值。這種最終循環的結構產生了“Rho 算法”的名稱，因為當值 x1 mod p、x2 mod p 等時，它與希臘字符 ρ 的形狀相似。

好的。現在讓我們深吸一口氣，看看上一段的真正含義。

假設我們在一條長長的圓形賽道上跑步。我們怎么知道我們已經完成了一個周期？一個聰明的解決方案是讓兩個跑步者 A 和 B 跑得比 A 快兩倍。他們從同一個位置開始，當 B 超過 A 時，我們知道 B 至少循環了一次。

我們有以下算法：

x = 2; y = 2; d = 1
while d == 1:
x = g(x)
y = g(g(y))
d = gcd(|x - y|, n)
if d == n:
return failure
else:
return d

假設我們想分解數字 8051。我們有

n = 8051
x = 2
y = 2
g(x) = (x^2 + 1)
g(g(x)) = g(x^2 + 1)

應用該算法，我們得到以下解決步驟：

迭代示例

?

從不同的 x 和/或 y 開始，我們可以找到 8051、83 的另一個除數

如果我們使用樸素的試因式分解算法，我們應該測試 N 的平方根以下的所有質因數。試制因式算法隨著數字 (2n/2) 的位數呈指數增長。

Pollard Rho 算法在其運行時間和它找到一個因子的概率之間提供了一種權衡。在 O(√d) <= O(n1/4) 次迭代中，可以以大約 0.5 的概率實現素數除數。這是一個啟發式的主張，對算法的嚴格分析仍然是開放的。

從理論到實踐

為了展示實際的算法（以及并行實現如何加速結果），我們準備了一個簡短的源代碼，使用一個 CPU、通過 OpenMP 的多個 CPU 和 GPU 運行 Pollard Rho 分解。提供了要分解的候選者列表，以顯示：

• 隨著因子的增長，算法如何變慢
• 放緩是如何歸因于因子大小，而不是因子數量
• GPU 開銷如何使并行算法在較小的因素上比 CPU 慢
• 正確選擇 GPU 的塊大小和塊數如何帶來更好的結果
• 并行算法的整體增益是多少。

?

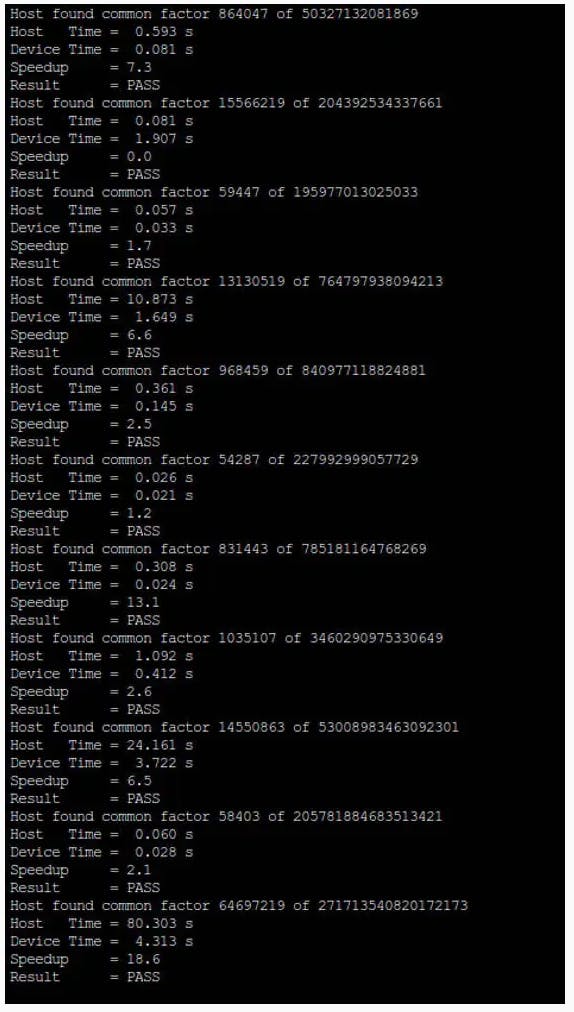
我們提出的算法僅限于 64 位數字，但很容易將其擴展到多精度算術。無論如何，眾所周知，Pollard Rho 的效率隨著因子的長度而降低：一般情況下，當 N 超過 40 位時，應選擇其他方法（如 P-1 和 ECM）。

該算法對于具有小因子的數字非常快，但在所有因子都很大的情況下較慢。The ρ algorithm's most remarkable success was the factorization of the eighth Fermat number , F 8 = 1238926361552897 * 93461639715357977769163558199606896584051237541638188580280321. The ρ algorithm was a good choice for F 8 because the prime factor p = 1238926361552897 is much smaller than the other factor. UNIVAC 1100/42 的分解耗時 2 小時。

您可以在我的FermatSearch網站上找到有關費馬分解和素數證明的更多信息。

CPU和GPU實現的區別

我們有兩個不同的內核作為主機和設備運行。

主機內核在 CPU（或啟用 OpenMP 時的 CPU）上運行。它需要對數字進行分解，然后循環直到找到解決方案。

設備內核在 GPU 上運行。x 和 y 的（隨機）值被預先計算、索引并存儲在數組中。數組在要分解的數字之后異步復制。然后啟動塊。設備代碼的每個線程同時訪問數組的一部分，計算其步長 (g(x), g(g(x)), 和的絕對值和 gcd)，然后將結果存儲回數組中，然后檢查 GCD 是否大于 1。如果是，我們有一個因子。該值保存在結果位置。一旦這個單程循環完成，結果就會被傳送回主機內存，并返回給調用主程序。

它的表現如何？

我們使用了 19 個數字的列表，并在 2 個不同的平臺上對它們進行了測試：一臺配備Intel Core i7 9800X處理器和Nvidia RTX 2060 GPU的 PC ，以及 Nvidia Jetson Nano板。

PC給出了以下結果：

Overall results:
Host?? Time = 503.134 s
Device Time =?? 1.576 s
Speedup???? = 319.2

換句話說，即使是 CUDA 中算法的簡單實現也顯示出 320 倍的加速。當我們有 1920 個計算單元時，我們在 GPU 上運行 256×256 網格，并且沒有利用共享內存加速或寄存器優化。

在 Nano 上，我們實現了以下時序：

Overall results:
Host?? Time = 1893.795 s
Device Time =?? 39.448 s
Speedup???? =?? 48.0

Nano 上的 GPU 是 Maxwell，具有少量內核和低于 1 GHz 的時鐘，但相對于 CPU，我們實現了 48 倍的加速。

我們還注意到，使用并行算法的 Jetson Nano 的 CUDA 比Intel 9800X 快 12 倍以上。對于成本比 PC 系統低 15 倍的電路板來說還不錯。

Github上提供了使用 Jetson Nano 試驗 CUDA 的源代碼。我們將很快測試其他背靠背 CPU vs GPU 算法，不僅展示并行計算的樂趣，也展示 CUDA 圖形加速的驚人之處。

?