Software-Defined-Radio (SDR) is a current communication research hotspot and the development direction. Digital modulation and demodulation are important content of SDR.
The SDR demodulation generally uses digital correlative demodulation. Digital correlative demodulation is the same with analog correlative demodulation, but its calculation is complicated. Discrete Fourier Transform (DFT) is used for digital signal analysis and processing. The paper is about a DFT-based algorithm for AM (DSB, SSB and VSB with strong carrier) signal demodulation. The main idea is to filter the digitalized AM signal received with BPF, then do DFT on samples in every one(or several) carrier circle to get the amplitude of AM signal and get rid of the zero frequency current. Compared with digital orthogonal demodulation framework, it is simple and easier to be realized for it doesn’t need to resume local carrier and filter with LPF in two branches. Simulation of this demodulation scheme indicates that noise-resisting property has been improved obviously. It is hopeful for this demodulation scheme to be applied to the design of AM signal digital receiver.
The paper also discussed the SSB, VSB signal modulation theory and simulation of the formation of SSB, VSB signal scheme.
KEYWORDS:software radio, digital demodulation,discrete fourier transform, Matlab
目 錄
摘要……………………………………………………………………………………III
ABSTRACT……………………………………………………………………………IV
第一章 緒論…………………………………………………………………………1
1.1 軟件無線電技術…………………………………………………………………1
1.1.1 基本原理…………………………………………………………………1
1.1.2 系統結構…………………………………………………………………2
1.2 軟件無線電的實際應用………………………………………………………3
1.3 軟件無線電中的調制解調技術………………………………………………5
1.4 課題設計內容…………………………………………………………………6
第二章 模擬調制信號數字化解調方案……………………………………………8
2.1 兩種解調方案…………………………………………………………………8
2.1.1 數字化正交解調…………………………………………………………8
2.1.2 基于DFT的數字化解調…………………………………………………10
2.2 方案比較……………………………………………………………………11
第三章 基于DFT的數字化解調系統結構…………………………………………12
3.1 A/D部分……………………………………………………………………12
3.2 帶通濾波器部分……………………………………………………………13
3.3 DFT運算部分…………………………………………………………………14
3.3.1 DFT公式的選擇…………………………………………………………14
3.3.2 DFT處理數字信號原理討論……………………………………………15
3.4 信號恢復部分………………………………………………………………16
第四章 模擬調制信號數字化解調實現與仿真…………………………………18
4.1 Matlab簡介與通信仿真……………………………………………………18
4.2 模擬調制信號的實現………………………………………………………19
4.2.1 AM信號調制算法與實現………………………………………………19
4.2.2 DSB信號調制算法與實現………………………………………………20
4.2.3 SSB信號調制算法與實現………………………………………………22
4.2.4 VSB信號調制算法與實現………………………………………………24
4.3 模擬調制信號數字化解調方法與仿真……………………………………26
4.3.1 AM信號解調方法與仿真……………………………………………………26
4.3.2 DSB信號解調方法與仿真……………………………………………………27
4.3.3 SSB信號解調方法與仿真……………………………………………………29
4.3.4 VSB信號解調方法與仿真……………………………………………………32
第五章 總結與展望………………………………………………………………33
5.1 方案設計優點與待改進之處………………………………………………33
5.2 總結…………………………………………………………………………34
5.3 收獲與心得……………………………………………………………………35
結束語…………………………………………………………………………………36 參考文獻……………………………………………………………………………37
附錄………………………………………………………………………………………38
摘 要
軟件無線電(SDR)是當前通信技術的一個研究熱點和發展方向。數字化調制、解調是SDR中的一個重要內容。SDR的解調一般采用數字相干解調的方法。數字相干解調法從原理上講與模擬相干解調法一樣,但計算量較大。離散傅立葉變換(DFT)是數字信號分析和處理中常用而有效的手段。該文提出便是一種基于離散傅立葉變換(DFT)的模擬調制信號(AM、DSB、插入強載波的SSB和VSB)數字化解調算法,方法是對采樣后的數字化信號進行帶通濾波后,按照每一個(或數個)載波周期內的采樣值進行離散傅立葉變換(DFT),求出載波的幅值,再除去直流分量。用Matlab語言編程,對前述模擬調制信號的基于DFT運算的解調方法進行了仿真研究,結果顯示該解調方案的抗干擾性能有所明顯改善。與數字化正交解調結構相比,省去了本地載波恢復,兩路低通濾波,簡單而易于實現,可望在采用AM信號方式的數字化接收機的設計中得到應用。
文中還討論了SSB、VSB信號的調制原理和在仿真中生成的SSB、VSB信號的方法。
關鍵詞:軟件無線電,數字化解調, 離散傅立葉變換,Matlab
ABSTRACT
第一章 緒論
1.1 軟件無線電技術
軟件無線電,顧名思義就是用現代軟件來操縱、控制傳統的”純硬件電路”的無線通信。軟件無線電技術的重要價值在于:傳統的硬件無線電通信設備只是作為無線電通信的基本平臺,而許多的通信功能則是由軟件來實現,打破了有史以來設備通信功能的實現僅僅依賴于硬件發展的格局。軟件無線電技術的出現是通信領域繼固定通信到移動通信,模擬通信到數字通信之后的第三次革命[1]。
1.1.1軟件無線電的基本原理
軟件無線電的基本思想就是將寬帶模數變換器(A/D,Analog/Digital,模/數)及數模變換器(D/A,Digital/Analog,數/模)盡可能地接近天線,建立一個具有”AD-DSP(Digital Signal Process,數字信號處理)-DA”模型的通用的、開放的硬件平臺,在這個平臺上盡量利用軟件技術來實現電臺的各種功能模塊[2]。如使用寬帶ADC(Analog Digital Convert,模數轉換器)通過可編程來實現各種通信頻段的選擇,如HF(High Frequency,高頻),VHF (Very High Frequency,特高頻),UHF(Ultra High Frequency,超高頻),SHF(Super High Frequency,甚高頻)等,通過軟件編程來完成傳送信號抽樣、量化、編碼、解碼運算處理和變換,以實現射頻電臺的收發功能;通過軟件編程實現不同的信道調制方式的選擇,如調幅、調頻、單邊帶、數據、跳頻和擴頻等,通過軟件編程實現不同的保密結構,網絡協議和控制終端功能等。軟件無線電是軟件化,計算密集型的操作形式。
從軟件無線電的技術實現來看,決定性的步驟在于將A/D和D/A變換器盡量向射頻端靠攏應用寬帶天線或多頻段天線,并將整個中頻段作A/D變換,這之后整個的處理都用可編程數字器件特別是軟件來實現。可看出,這樣一個體系結構具有非常大的通用性。對解決上面提到的問題有很大的潛力,可用來實現多頻段、多用戶和多體制的通用無線通信系統。要實現以上系統,對天線,高速A/D變換器和高速的數字信號處理器和通用CPU(Central Processing Unit,中央處理器)的要求都很高。
上述要求在以前(甚至某些要求對現在)都幾乎是不可實現的。然而我們可以參考個人計算機領域的經驗,在個人微機的概念提出初期,計算機行業也是各種不同的機器相互競爭,沒有什么標準可言。由于當時的微電子技術還很落后,大多數人認為個人擁有計算機是不現實的。僅僅過了十幾年的時間,微電子技術的發展已經使得個人微機成為了當今最熱門的產業,而那些在發展初期沒有抓住時機的公司和國家也遠遠地落后了。如今微機領域的競爭早以將重點轉移到了軟件的競爭上了。而下個世紀的個人通信系統將很有可能是一個具有驚人處理能力和標準射頻接口的通用硬件平臺,依靠不同的軟件提供異常豐富的功能和服務,也就是說通信領域將經歷類似于個人微機在八九十年代所經歷的變革,而現在正是這一變革的關鍵時刻。
軟件無線電這一概念提出的背景是[3]:
1.硬件工藝水平提高很快,A/D/A、DSP和CPU等的性能越來越好。
2.新的通信體制和標準不斷提出,通信產品的生存期縮短,開發費用上升,傳統的通信體制很難適應。
3.各種通信體制共存,對多種體制間的互聯要求也日趨強烈。這一點在軍事通信中表現尤為突出,也是軟件無線電首先在軍事領域得到發展的主要原因。
4.無線頻帶越來越擁擠,對通信系統的頻帶利用率和抗干擾能力要求不斷提高。沿著現在通信系統的發展方向,很難對頻帶重新規劃,采用新的抗干擾方法需要對系統結構做較大改動,代價很大。
1.1.2 軟件無線電的系統結構
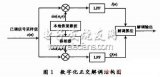
由圖1.1可看出,所謂軟件無線電,其關鍵思想以及與傳統結構的主要區別在于:
1.將A/D和D/A向RF(Radio Frequency,射頻)端靠近。由基帶移到中頻。對整個系統頻帶進行采樣。
2.用高速的DSP/CPU代替傳統的專用數字電路與低速DSP/CPU做A/D后的一系列處理。以上兩點僅僅是結構上的區別。
圖1.1 軟件無線電系統結構簡圖
隨著微電子技術的發展,各種數字器件的性能不斷提高,現有的數字無線電也會不斷發展,也將使得A/D/A一步步地向RF端靠近。那么軟件無線電會不會僅僅是數字無線電的進一步發展呢?回答是否定的。我們認為:軟件無線電和數字無線電的進一步發展在概念上是不同的。這主要是因為A/D/A的移向RF端只是為軟件無線電的實現提供了必不可少的條件,而真正關鍵的步驟是采用通用的可編程能力強的器件(DSP、CPU等)代替專用的數字電路。由此帶來的一系列好處才是軟件無線電的真正目的所在。
軟件無線電的最終目的就是要使通信系統擺脫硬件系統結構的束縛。在系統結構相對通用和穩定的情況下,通過軟件實現各種功能,使得系統的改進和升級非常方便且代價小,且不同的系統間能夠互聯和兼容。而數字無線電的進一步發展并不能做到這一點[4]。它只能導致對硬件和系統結構更多的依賴。不過,目前軟件無線電更多地是以一種概念和猜想的形式出現,具體的定義和體系結構尚無定論。可以說除了上面提到的兩點關鍵思想被普遍接受以外,其它各方面的內容都在爭論和探討之中。而本文所討論的就是軟件無線電中的數字化調制解調技術,其他方面不做進一步的討論。
1.2 軟件無線電的實際應用
軟件無線電作為一門新興的技術,目前的應用領域有:
1.蜂窩移動通信系統
在蜂窩移動通信系統中,基站和移動終端采用軟件無線電結構,硬件簡單,功能由軟件定義。射頻頻段、信道訪問模式及信道調制都可編程。在此系統中,軟件無線電的發射與其它系統不同,它先劃分可用的傳輸信道,探測傳播路徑,進行適合信道的調制,電子控制發射波束指向正確的方向,選擇合適的功率,然后再發射。接收也同樣如此,它能劃分當前信道和相鄰信道的能量分布,識別輸入傳輸信號的模式,自適應抵消干擾,估計所需信號多徑的動態特征,對多徑的所需信號進行相干合并和自適應均衡,對信道調制進行柵格譯碼,然后通過FEC(Forward Error Correct,前向糾錯)譯碼糾正剩余錯誤,盡可能降低誤比特率。此外,軟件無線電能通過許多軟件工具增加增值業務。這些軟件工具能幫助分析無線電環境,定義所需的增加內容,在無線環境下,測試由軟件開發增值業務的樣板,最后再通過軟件或硬件開放該增值業務。
2.智能天線
智能天線最初用于雷達、聲納及軍事通信領域,由于價格等因素,一直未能普及到其它通信領域。近年來,數字信號處理技術迅速發展,數字信號處理芯片的處理能力不斷提高,芯片價格已可接受。同時,利用數字技術可在基帶形成天線波束,取代了模擬電路,提高了天線系統的可靠性和靈活程度。在我國的TD-SCDMA(Time Division-Synchronous Code Division Multiple Access,時分同步的碼分多址技術)方案中,基站采用智能天線技術,利用數字信號處理技術識別用戶信號到達方向,形成天線主波束。
引入SDMA(Spase Division Multiple Access,空分多址)方式后,根據用戶信號不同的空間傳播方向,提供不同的空間信道。采用數字方法對陣元接收信號加權處理,形成無線波束,使主波束對準用戶信號方向,干擾信號方向形成天線方向零缺陷或較低的功率增益,達到抑制干擾目的。
使用智能無線的優勢在于:無線波束賦形的結果等效于提高天線的增益;天線波束賦形后,可大大減少多徑干擾;信號到達方向提供了用戶終端的方位信息,用于實現用戶定位;用多個小功率放大器代替大功率放大器,降低了基站成本,提高了設備可靠性。
3.多頻多模手機
在歐洲的ACTS FIRST(Acoustic Control and Telemetry System,聲控制與遙測系統)項目中,將軟件無線電技術應用于設計多頻/多模(可兼容GSM(Global System of Mobile,全球移動系統))、 CDMA(Code Division Multiple Access,碼分多址) 及現有的大多數模擬體制)可編程手機。它可自動檢測接收信號,接入不同的網絡,而且能滿足不同接續時間的要求。軟件無線電技術可用不同軟件實現不同無線電設備的各種功能,可任意改變信道接入方式或調制方式,利用不同軟件即可適應不同標準,構成多模手機和多功能基站,具有高度的靈活性。
它的出現,使通信的發展經歷了由固定到移動,由模擬到數字,由硬件到軟件的三次變革。軟件無線電技術正越來越廣泛應用于移動通信領域,在第二代移動通信系統向第三代移動通信系統過渡過程中,軟件無線電技術將發揮重要作用。
4.衛星通信
在當今通信領域中,衛星通信是最重要的通信方式之一。但是,由于目前衛星通信系統設備種類繁多,設備管理和維護工作復雜,使得衛星通信系統更新換代周期長,不能很好地適應現代高科技的發展步伐。而軟件無線電以其軟件定義功能和開放式模塊化結構的技術思想能很好地解決衛星通信系統存在的問題,因此,研究具有軟件無線電特征的衛星通信系統是很有意義的。
在衛星通信系統中,系統功能主要指多址方式、網絡結構、組網協議和通信業務等;而設備功能指接口標準、調制解調方式、信道編碼方式、信源編碼方式、信息速率、復用方式等。軟件無線電技術思想就是采用先進的技術手段,使得上述功能可以用軟件來定義。通過友好的人機界面,人們可以在不改變硬件設備的情況下實時地改變通信系統的功能,從而使該系統能適應各種應用環境,因而具有很強的適用性和靈活性。
考慮到衛星通信頻帶寬,信息速率高且變化范圍大的特點,在目前的計算機技術水平上,如果設備功能全由軟件來實現,由于軟件的逐條運行指令的特點,即使采用多處理器來協同運算,也無法實現高信息速率下的實時處理,使其在衛星通信中的使用范圍受到了限制。
軟件無線電技術在商用通信領域中的應用前景非常廣闊,目前軟件無線電技術已在800MHz商用蜂窩無線頻段、衛星通信等領域中得到應用,作為一種強有力的結構框架,有助于我們提供先進、經濟的無線業務。軟件無線電也存在一些缺點,如很難設計寬頻帶、低損耗天線和射頻變頻器;很難估計在實用中對處理能力的需求和可再編程DSP/CPU處理能力的配置;較難保證內部處理器接口的數據速率。目前軟件無線電結構關鍵部件還沒有開放結構標準。DSP功能庫還不能象混合和匹配VME(Versamodel Eurocard,一種傳統電信設備總線)板那樣,對來自不同軟件供應商的實時軟件進行混合和匹配。但隨著現代通信技術的飛速發展,這些缺點中大部分是可以避免的,并可以在克服這些障礙的同時,進一步降低成本,使軟件無線電臺早日投放市場。
1.3 軟件無線電中的調制解調技術
調制解調技術在近幾十年中得到了不斷的發展和完善,總的來說可以分為兩大類:單音調制和多音調制。單音調制方式即在某一時刻用輸入數據對單一載波的不同分量(如幅度、頻率、相位等)進行調制,因此也稱為單載波調制。多音調制通常是將原始信道劃分為等間隔的多個正交子信道,每個子信道使用不同的載波進行調制,故多音調制也稱為多載波或多路并行調制,有時也稱為OFDM(Orthogonal Frequency Division Multiplexing,正交頻分復用)。
由于單載波調制技術比較成熟,所以目前的數據通信系統中多采用這種調制方式。但自從1971年Weinstein、Ebert等人提出將DFT用于多音調制系統中的頻分復用以后,多音調制技術受到了越來越廣泛的關注[5]。相對單音調制來說,它具有如下特點:采用多音調制方案與采用判決反饋均衡的單音調制方案所得到的最大傳輸速率近似相等。然而,對于存在失真、衰落或非白噪聲的信道來說,多音調制可以獲得更高的傳輸速率;由于多音調制具有多路并行的特點,使得其調制信號在接收端不需進行任何特殊的處理,即可獲得相當于單音調制解調系統在接收端采用信道均衡后所得到的信噪比或信號干擾比;為了能夠獲得更佳的傳輸性能,可以在多音調制系統中采用均衡技術,由于每個窄帶子信道中的信道特性近似是線性的且脈沖響應拖尾較少,使得多音調制的均衡較單音調制的均衡簡單得多;相位抖動在單音調制系統的接收端將引起信號在空間的旋轉,從而嚴重地影響了判決:而在多音調制系統中,相位抖動所引起的失真均勻地分布在各個子通道中,使得其影響大大地減弱了;在傳輸速率相同的情況下,由于多音調制系統中的碼元周期較長,使得脈沖干擾對它的影響遠弱于對單音調制的影響;在單音調制系統中,對于單頻干擾較為敏感,而在多音調制系統中各子信道可以根據各自信噪比大小傳送不同的比特數,并可封閉干擾嚴重的信道,這樣既能充分地利用頻帶,又可克服多種干擾。
軟件無線電中信號的調制與解調是研究的重點問題之一。在通用的硬件平臺上,采用不同的軟件算法來實現不同調制與解調是軟件無線電的核心思想。
在軟件無線電系統中,調制和解調都是用程序來實現的(也稱為全數字化調制解調)。要編寫出各種類型調制信號的調制解調軟件,關鍵是確定信號處理算法。可以利用FPGA(Field Programmable Gate Array,現場可編程邏輯器件)來實現需要的調制解調算法,其計算速度比DSP更快,但是靈活性及控制功能較差,需要與DSP或單片機配合使用。最新的一項技術是可以利用DFT(Discrete Fourier Transform,離散傅立葉變換)來實現數字化調制解調算法,這是一種不需要本地載波的方法,本文將做重點介紹。
建立調制解調算法及程序的一條途徑是把模擬電路的工作原理軟件化。比如要對AM(Amplitude Modulation,調幅)信號進行相干解調,或建立載波同步,乘法器,低通濾波等軟件模塊的做法雖然可行,但是計算量很大。實際上,根據軟件無線電的特點,可以建立與調制解調電路工作原理有所不同的調制解調算法。本問所提出的便是一種不同的調制解調算法–基于DFT的模擬調制信號數字化解調算法。
綜上所述,軟件無線電中信號的調制與解調是研究的重點問題之一。
1.4課題設計內容以及研究目的與意義
數字化調制是指用軟件產生出調制信號的樣值序列,再通過D/A轉換得到模擬的調制信號,數字化解調則是指對已調波信號進行A/D轉換,再通過數據處理來實現對信號的解調。數字化調制、解調是SDR(Software-Defined Radio,軟件無線電技術)中的一個重要內容。SDR主要依靠軟件來完成接收系統的各項功能,如調制解調、智能天線、信號識別等,其優點在于可以使產品的硬件大大簡化,可靠性大大提高,便于生產和維護,可以通過更新軟件來實現產品的功能升級等。SDR是當前通信技術的一個重要研究領域和發展方向。
本次畢業設計題目為:模擬調制信號數字化解調技術研究
具體要求:
1.對SDR的基本概念進行研究,重點是數字化解調技術。
2.設計一個基于離散傅立葉變換的AM信號數字化解調算法
3.用MATLAB語言編程產生出AM信號,并實現數字化解調。
4.對DSB、SSB、VSB信號的數字化調制和解調方法進行研究。
本課題的研究內容涉及軟件無線電中的數字化解調方法,作者將現有的基于離散短時傅立葉變換(DSTFT)的AM信號數字化解調方法引入到通信系統中廣泛使用的解調中,并進行改進,從而提出了一種基于離散傅立葉變換(DFT)的AM信號數字化解調方法。作者還采用MATLAB語言編程對解調系統進行了仿真實驗,驗證了其可行性和抗干擾性能(信噪比)。基于DFT的AM信號數字化解調方法的意義在于兩個方面,首先這種解調方法不需要像現有的采用數字化正交解調方法來解調AM信號那樣需要本地載波提取和兩個低通數字濾波器,從而大大降低了解調算法的計算量;其次是與傳統的AM信號解調方式相比,在相同的輸入信噪比情況下,在一定程度上改善了解調器的性能。
文章做如下安排:我們將在第二章講述兩種常用的模擬調制信號數字化解調方案:數字化正交解調和基于DFT的數字化解調,并且對方案進行了比較,最后選擇一種優勢明顯的方案–基于DFT的數字化解調。第三章論述了基于DFT的數字化解調方案的系統結構,詳細介紹了各個部分的功能與其理論知識。從第四章開始,論述了模擬調制信號的調制算法和解調算法,并用Matlab實現了仿真。最后總結了在設計過程中的不足與待改進之處,分析了設計的前景,并對下一步工作進行了展望。
第二章 模擬調制信號數字化解調方案
2.1 兩種解調方案
軟件無線電已成為現代通信技術研究的新課題,它的基本思想是在一個通用的硬件平臺上,通過安裝不同的軟件來實現不同的通信功能。軟件無線電具有開放式模塊化結構,它主要由寬帶A/D&D/A 、可編程DSP模塊、窄帶A/D&D/A 、用戶終端等組成[6]。在接收時,來自天線的信號經過RF處理和變換,由寬帶A/D數字化,然后通過可編程DSP模塊實現各種所需的信號處理,并將處理后的數據送至多功能用戶終端;同樣,也可通過類似的流程將數據通過天線發射出去。另外,利用在線和離線軟件,軟件無線電還可以實現通信環境的分析、管理以及業務和性能的升級。軟件無線電的一個主要特點是完全可編程性,即RF頻段和帶寬、信道接入方式、傳輸速率、接口類型、業務種類、加密方法等均可由軟件編程來改變。
軟件無線電的開放式模塊化結構為調制解調的實現提供了一個良好的軟硬件平臺,但同時也對調制解調提出了更高的要求,即要求所采用的調制解調方法能夠適應不同的頻帶寬度以及不同的傳輸速率。為此,如何設計一種調制解調技術來滿足軟件無線電的需求將是本文所要討論的主要問題。當代無線通信各種技術發展很快,各種通信系統的調制方式也很多,有AM、FM(Frequency Modulation,調頻)、DSB(Double Side Band,雙邊帶調制信號)、FSK(Frequency Shift Key,頻移鍵控)、PSK(Phasic Shift Key,相移鍵控)等,其多址方式有時分多址、頻分多址和碼分多址等。各通信系統的調制方式、多址方式、通信協議等的不同導致各通信系統接收機之間差別很大,一個接收機只能滿足某些特定的需求,而無法滿足各種需要,因此增加接收機的通用性非常有意義。這其中對信號的接收處理是實現通用性的關鍵。為了實現通用性,本文使用介紹兩種常用的數字化解調的方法對信號進行處理。
2.1.1 數字化正交解調
下面首先介紹數字化正交解調方案。數字正交解調方案廣泛應用與軟件無線電接收機中[5]。對于AM信號,基帶解調算法為 。對LPF(Low Pass Filter,低通濾波器)的輸出進行數據抽取是因為基帶信號I(In-phase)、Q(Quadrature)需要的采樣率遠低于對調制信號的采樣率。這種解調方案利用軟件中可以實現的平方和開方運算而免去了復雜的載波同步過程,不僅減少了計算量,也避免了因載波同步誤差而引起的解調誤差(相位同步誤差和比較小的頻率同步誤差都不影響解調效果)。因為仍然是相干解調,所以這種解調方案具有良好的抗干擾性能。
傳統的正交解調電路采用模擬器件,由此引入的一系列模擬器件所固有的誤差降低了正交解調器的性能,例如增益平衡度、正交平衡度、直流偏移、阻抗匹配以及本振泄漏等。如今,傳統的模擬解調機制正在被數字化解調逐步代替,從而提高了系統的穩定性和信號分析的靈活性。
圖2.1 數字正交解調方案
正交調制解調算法可以使用幾乎相同的硬件電路,只通過對幅度和相位進行不同的軟件處理即可實現對不同調制信號的解調,滿足軟件無線電的設計要求。實際中一般采用FPGA和DSP協同工作的結構,FPGA主要完成下變頻、濾波抽取等需要在高速率下完成的工作,也就是解調算法的硬件通用部分,DSP負責對不同的調制信號的幅度和相位作最后的軟件解調算法。綜上所述,正交解調算法具有一定的理論及現實應用價值。
圖2.1是數字正交解調電路的一種基本模型,這是一個通過數字化的解調器,對不同類型的調制信號需要使用不同的基帶解調算法。對于AM信號,基帶解調信號需要完成采樣數據抽樣(使低通濾波器輸出信號的采樣頻率降低),計算載波幅值等工作。輸入的模擬中頻信號首先經過AD變換,實現數字采樣,其數據流分兩路通過數字乘法器分別與本地數字振蕩器產生的cos分量和sin分量相乘,實現輸入信號在頻域的搬移,即載波頻率為零,隨后進入數字低通濾波器,并根據信號帶寬進行抽取,得到同相分量I和正交分量Q兩路基帶信號,從而實現中頻信號的下變頻和兩路正交基帶信號的獲得。上述過程可以數學表達式的形式說明,AD變換后的信號以正交形式表示:
(2.1)
其中 分別是信號的同相分量和正交分量, 是輸入中頻信號的載波頻率, 通過與數字振蕩器信號
(2.2)
相乘便可實現下變頻:
(2.3)
經過數字低通濾波器濾除二次諧波分量后即可得到期待的兩路基帶信號:
(2.4)
根據不同的信號處理要求,輸出結果由FPGA加上DSP做進一步的處理。由于數字本振、數字混頻和數字濾波器的應用,電路的穩定性得到了很好的保證,通過改變數字本振的頻率和相位、數字濾波器的通帶特性,能夠方便靈活地獲得輸入中頻信號的幅度和相位特征,并且具有很好的一致性。
正交解調技術在雷達、聲納、通信等領域有著廣泛的應用。 基于直接中頻采樣技術的全數字化正交解調方法近年來得到了廣泛的研究和應用。
2.1.2 基于DFT的數字化解調
文獻[2]提出一種在軟件無線電中基于離散傅立葉變換(DFT)算法的幅度調制信號(AM)數字化解調算法,方法是對采樣后的數字化AM信號進行帶通濾波器后,按照每一個(或數個)載波周期內的采樣值進行離散傅立葉變換(DFT)求出載波的幅值,在去掉直流量。與數字化正交解調結構相比,省去了本地載波恢復,兩路低通濾波,簡單而易于實現,該解調方案仿真結果表明抗干擾性能也有所改善,可望在采用AM信號方式的數字化接收機的設計中得到應用。
基于DFT的AM信號數字化解調框圖如圖2.2所示。與圖2.1相比較,去掉了復雜的載波恢復,不需要進行兩路低通濾波,解調過程實現起來容易得多。
AM信號是使載波信號的包絡輸入調制信號呈線性對應關系,在接收方只要能夠將載波的包絡值提取出來即可恢復原來的調制信號。
圖2.2 基于DFT的AM信號數字化解調框圖
在該算法中,首先對采樣后的數字化AM信號進行帶通濾波,取出帶外信號,并對噪聲有一定的抑制效果,然后進行DFT解調恢復;設采樣頻率AM信號的載波頻率的m倍,即每個載波周期采樣m個點,m是大于或等于3的整數,每取得m格采樣數據(記為 )進行一次DFT,求出載波幅值:
(2.5)
(2.6)
(2.7)
由DFT的性質可知,序列 就是AM信號包絡的采樣值,只要求出并去掉其中的直流成分便可正確恢復原信號。
2.2 方案比較
前面所述的數字化正交解調方法存在如下缺點:
首先要進行本地載波恢復,且本地載波和信號載波之間的頻率偏差超出一定范圍時,會導致信號超出數字信道而發生失真;
其次計算量大,因為對每一個采樣值要分兩路乘法和階數較高的低通濾波:與本地載波的相乘之后要進行兩路低通濾波器來提取同相分量和正交分量;
最后是由于這種解調方案只是對傳統的相干解調方法的數字化實現,其抗干擾性能沒有得到改進。其本振、混頻、低通濾波均采用模擬技術實現,數字化在I、Q基帶信號生成之后進行。由于模擬器件的一致性及穩定性等因素,兩路正交通道間幅度一致性及相位正交性難以做得很好;此外,基帶采樣還容易受零漂、1/f噪聲的影響。這些將導致系統性能的下降。而本文后面所提出的基于DFT的AM信號數字化解調方法則省去了載波恢復,碼元確定時,是一種簡單實用的算法。
與數字化正交解調結構相比,基于DFT的數字化解調方案計算量大大降低,對采樣數據基本上只做加減運算,每8個采樣點才做一次平方、開方運算;采用較低的采樣頻率也可以正常解調;省去了本地載波恢復,兩路低通濾波,簡單而易于實現,該解調方案仿真結果表明抗干擾性能也有所改善,可望在采用AM信號方式的數字化接收機的設計中得到應用。
第三章 基于DFT的數字化解調系統結構
如第二章所述,基于DFT的數字化解調系統結構分為四個主要的部分,A/D,帶通濾波器,DFT運算以及信號恢復部分。
3.1 A/D部分
隨著通信技術的迅速發展以及計算機的廣泛應用,利用數字系統處理模擬信號的情況變得更加普遍。數字電子計算機所處理和傳送的都是不連續的數字信號,而實際中遇到的大都是連續變化的模擬量,模擬量經傳感器轉換成電信號的模擬量后,需經模/數轉換變成數字信號才可輸入到數字系統中進行處理和控制,因而作為把模擬電量轉換成數字量輸出的接口電路A/D轉換器是現實世界中模擬信號向數字信號的橋梁。
采樣是模擬信號數字化的第一個步驟,研究的重點是確定合適的采樣頻率,使得既要能夠從采樣信號(采樣序列)中無失真地恢復原模擬信號,同時又盡量降低采樣頻率,減少編碼數據速率,有利于數據的存儲、處理和傳輸.從”在采樣信號的頻譜中要完整地保留原模擬信號的頻譜”的要求出發,提出了兩種采樣方式,即低通信號采樣和帶通信號采樣。
1.低通信號采樣:如果被采樣信號是(或者看成是)低通信號,則只要選取采樣頻率 ( 是模擬信號的截止頻率),則采樣信號的頻譜中就完整地保留了原模擬信號的頻譜,只要讓采樣信號通過一個理想低通濾波器就能夠無失真地恢復原模擬信號。如果 ,則稱為過采樣.
2.帶通信號采樣(欠采樣):如果被采樣信號是帶通信號(中心頻率大于帶寬),則只要按照下面的條件
(3.1)
來選擇采樣頻率。
其中, 是帶通信號的下限頻率, 是帶通信號的上限頻率,n是的整數部分,也可記為 表示帶通信號的帶寬,則采樣信
的頻譜中就完整地保留了原帶通信號的頻譜,只要讓采樣信號通過一個理想帶通濾波器就能夠無失真地恢復原帶通信號。對于窄帶信號欠采樣的采樣頻率只需要稍大于帶寬的2倍就行了。各種已調波信號實際上都可以看作是帶通信號,是否可以按照帶通信號采樣的情況來確定一個很低的采樣頻率,從而取得很低的數據速率呢?作者認為答案是否定的。因為在軟件無線電中,對已調波信號進行采樣的目的不是要從采樣信號去恢復原來的信號,而是要用采樣信號來進行解調(通過欠采樣直接恢復基帶信號只是特例,幾乎沒有實際意義),所以對采樣速率的選擇必須考慮到解調過程(包括位同步等操作)的要求,而不能盲目地套用帶通信號采樣的公式。
現代應用中經常要求對模擬信號采樣,將其轉換為數字信號,然后對其進行計算處理,最后再重建為模擬信號。而基于DFT的模擬調制信號數字化解調的方案采用MATLAB作為仿真工具:取AM信號為多音信號,頻率為:1000Hz,2000Hz,3000Hz。載波頻率為:10000Hz,根據采樣定理,我們取采樣頻率至少為20000Hz。
具體信號為:
(3.2)
載波信號:
(3.3)
AM信號為:
(3.4)
3.2 帶通濾波器部分
數字濾波器是具有一定傳輸選擇特性的數字信號處理裝置,其輸入、輸出均為數字信號,實質上是一個由有限精度算法實現的線性時不變離散系統。它的基本工作原理是利用離散系統特性對系統輸入信號進行加工和變換,改變輸入序列的頻譜或信號波形,讓有用頻率的信號分量通過,抑制無用的信號分量輸出。
數字濾波器和模擬濾波器有著相同的濾波概念,根據其頻率響應特性可分為低通、高通、帶通、帶阻等類型,與模擬濾波器相比,數字濾波器除了具有數字信號處理的固有優點外,還有濾波精度高(與系統字長有關)、穩定性好(僅運行在0與l兩個電平狀態)、靈活性強等優點。數字濾波器按單位脈沖響應的性質可分為無限長單位脈沖響應濾波器和有限長單位脈沖響應濾波器兩種。
基于MATLAB的信號處理工具箱為數字濾波器設計帶來了全新的實現手段,設計快捷方便,仿真波形直觀。上述三種設計方案均可實現設計指標,但以直接原型變換法最為簡便。實際應用中,數字濾波器也可以對連續時間信號進行處理,但需要先對連續信號進行A/D變換,經數字濾波后,再經D/A轉換得到所需要的連續信號。
MATLAB提供了多種FIR數字濾波器的設計方法。選用ParksMcClellan最優濾波器設計是在與其他類型的濾波器進行仿真比較后決定的。作者用窗函數法中的fir1函數進行設計,濾波后的波形延遲比較大,而且在穩定區內的波形也有所削弱。用基于最小二乘約束設計方法的fircls函數進行設計,仿真結果表明碼元穩定區的波形幅度有所減少,而采用cremez函數設計出來的濾波器是非線性相位的,升余弦函數則主要是低通濾波。所以選用了ParksMcClellan設計算法。將上述帶通濾波器應用于AM信號的數字化解調仿真系統,取得了比較滿意的結果。
3.3 DFT運算部分
傅立葉變換在通信與控制系統的理論研究和實際應用之中,采用頻率域(頻域)的分析方法比經典的時間域(時域)方法有許多突出的優點。當今,傅里葉分析方法已成為信號分析與系統設計不可缺少的重要工具。20世紀70年代,出現的各種二值正交函數(沃爾什函數),它對通信、數字信號處理等技術領域的研究提供了多種途徑和手段。使人們認識到傅里葉分析不是信息科學與技術領域中唯一的變換域方法。
DFT開辟了頻域離散化得到了,使數字信號處理可以在頻域采用數字運算的方法進行,這樣就大大增加了數字信號處理的靈活性。更重要的是DFT有多種快速算法。統稱為快速傅立葉變換(FFT,Fast Fourier Transform)。從而使信號的實時處理和設備的簡化得以實現。因此,時域離散系統的研究與應用在許多方面取代了傳統的連續時間系統。所以說,DFT不僅在理論上有重要的意義,而且在各種信號的處理中亦起著核心的作用。
3.3.1 DFT公式的選擇
目前關于DFT存在著兩套公式,在大多數著作和文獻中給出的公式為:
(3.5)
(3.6)
在少數著作中給出的公式為:
(3.7)
(3.8)
這兩套公式是成對的,即每套公式中正變換成立,則逆變換也一定成立,反之亦然。它們的差別僅僅在于系數I/N的位置不同,前者將之放在DFT中,而后者將之放在IDFT中。那么它們有什么區別呢?應當如何選擇呢?實際上,公式(3.5)采用的是零延拓原理,是對有限序列采用傅立葉變換了分析而得到的,它代表FT譜的”抽樣值”,反映有限長序列的總體量,與序列的長度有關;而公式(3.7)是時限信號x(t) ( )周期延拓后的傅立葉系數近似值,它反映的是信號的平均性質,與序列的長度無關。在具體選用時,應根據實際情況來選擇使用哪種公式。
在AM信號的數字化解調算法中,采用的DFT公式是(3.7),好處在于:該公式的計算結果(載波的幅值)與有限序列的長度無關,即其值不會隨著DFT點數的增多而大幅度變化,這樣概念上就比較直觀、正確,同時可以避免由于采樣點數太多而發生數據溢出(求和可以分段進行,對每段的和先除以系數再相加,避免總的和數發生溢出)。當然如果確信不會發生求和數據發生溢出,采用公式(3.5)也是可以的。
3.3.2 DFT處理數字信號原理討論
首先需要了解DFT處理數字信號的過程和原理對幅值A ,頻率為 、初相為 的正弦波按采樣頻率f進行均勻采樣,每周期采樣點數 ,則得到時域離散周期序列,其主值序列為:
(3.9)
其中n=0,1,…N-1
根據定義對x(n)進行離散傅立葉變換(這里選取公式3.7),為保證頻譜分析的準確性,取變換區間長度為N,則有:
(3.10)
其中,
根據該計算式可得到頻域的離散序列X(0),X(1) …. X(N-1)當時域波形為正弦函數時,它所對應的傅立葉變換是一對沖激函數,即只有基波分量X(1)不為零.將 帶入公式(3.7),并根據歐拉公式作數學推導,求解X(1):
(3.11)
(3.11)即是基波分量的數學表達式,首先可以看出頻域基波分量的幅度只與時域波形的峰值存在線性關系,而與采樣點數不存在關系。其次,還可以發現初相位 對基波的幅度沒有影響,這一點很有意義。
為了分析相頻特性,將X(1)分解成實部與虛部:
(3.12)
可以解得正弦信號的幅值為
(3.13)
由此可知DFT運算完全可以提取出正弦信號的幅度信息。
由(3.13)式可以看出,解出的正弦信號的幅度值與(2.5)式得出的結果是一樣的。由此可知,基于DFT的數字化解調系統方案是可行的。
3.4 信號恢復部分
在軟件無線電、雷達等系統中,通常需要對帶通信號進行數字化,為了降低后續數字信號處理的數據量,可以采用均勻欠采樣和非均勻采樣技術。關于均勻采樣技術,很多文獻都有論述對于非均勻采樣,由于信號的采樣間隔不均勻,傳統的均勻采樣定理不再適用。如何選取采樣參數及如何根據非均勻采樣序列重建帶通信號是這種處理方法的一個基本問題。文獻用多維線性系統理論研究了帶限信號的m階采樣和重建問題。文獻討論了帶通信號的M階非均勻采樣理論,它采用M個相互錯開的均勻采樣序列以2/m倍的信號帶寬為采樣頻率對信號進行采樣。文獻[5]中采樣頻率為帶通信號非均勻采樣的最小采樣頻率(奈奎斯特速率),當m為奇數時,要求信號下截止頻率為信號帶寬的整數倍;當m為偶數時,對信號的頻帶位置沒有要求。本文將帶通信號非均勻采樣的采樣頻率范圍進行了拓寬,研究了頻譜混疊和信號重建。
對于帶限信號,只要滿足采樣定理,就可以用時域上的采樣信號完整的重建出來。對于時限信號,可以通過頻域上的采樣樣本X(k/T)完整的表示出來,這里T為信號的時域長度; 對于時限信號,可以對時域上有限個采樣樣本或者頻域上有限個采樣樣本完整的表示出來。也就是說,可以通過對時域上有限個樣本進行變換,得到頻域上的表示,并且不會丟失任何信息。 因此,我們可以對時域信號進行加窗,到達近似時限信號。直接將信號截斷,相當于矩形窗。只有采用了加窗之后,才能實現時限,這樣才能在頻域上的譜線表示(采樣表示)出來。因此,才能使用DFT/FFT進行計算。
本文對低通和帶通信號的采樣及重建進行了理論分析,指出當用最低采樣頻率2B(2倍信號帶寬)進行采樣時,如果信號的邊緣頻率分量(即信號的最高及最低頻率分量)為沖激函數,則大多數條件下不能精確重建原信號,而如果邊緣頻率分量為有限值,盡管此時信號頻譜發生混疊,仍然能夠精確重建原信號.結論不僅適用于帶通信號,也同樣適用于低通信號.
實際應用中,一方面,不論帶通信號還是低通信號,如果已知待采樣信號的邊緣頻率分量不含沖激函數,采樣頻率可以選擇2B,此時的頻譜雖然發生了混疊,仍然能夠重建原信號;另一方面,如果預先無法得知待采樣信號的邊緣頻率分量是否含有沖激函數,選擇的采樣頻率最好大于2B,這樣就不會引起頻譜混疊,且當邊緣頻率為沖激函數時,也能精確重建原信號.
帶通信號廣泛應用于通信、雷達、聲納等領域,在這些領域中常常需要對信號進行數字化處理。傳統的數字化方法是對信號進行均勻采樣,均勻采樣理論已很成熟。另一種方法是對信號進行高階周期性非均勻采樣,由于信號的采樣間隔不均勻,傳統的采樣定理不再適用,如何根據非均勻采樣序列重建帶通信號是這種信號處理的一個基本問題。許多文獻都對這個問題進行了探討,它們都是從消除信號的頻譜遷移項之間頻譜混疊出發討論信號的重建問題。文獻用多維線性系統理論討論了帶限信號的廣義采樣問題,本文將文獻中的廣義采樣定理從帶限信號擴展到帶通信號,討論了非均勻采樣時帶通信號的重建問題;將帶通信號重建像函數計算變成了一個線性方程組求解問題,利用克拉默法則(Cramer’s rule),通過求解線性方程組得出重建像函數;最后給出了計算機仿真實例。
第四章 模擬調制信號數字化解調實現與仿真
4.1 MATLAB簡介與通信仿真
MATLAB語言是一種廣泛應用于工程計算及數值分析領域的新型高級語言,自1984年由美國MathWorks公司推向市場以來,歷經十多年的發展與競爭,現已成為國際公認的最優秀的工程應用開發環境。MATLAB功能強大、簡單易學、編程效率高,深受廣大科技工作者的歡迎。
在歐美各高等院校,MATLAB已經成為線性代數、自動控制理論、數字信號處理、時間序列分析、動態系統仿真、圖像處理等課程的基本教學工具,成為大學生、碩士生以及博士生必須掌握的基本技能。
MATLAB特點:
1.數值計算和符號計算功能
MATLAB的數值計算功能包括:矩陣運算、多項式和有理分式運算、數據統計分析、數值積分、優化處理等。符號計算將得到問題的解析解。
2.MATLAB語言
MATLAB除了命令行的交互式操作以外,還可以程序方式工作。使用MATLAB可以很容易地實現C或FORTRAN語言的幾乎全部功能,包括Windows圖形用戶界面的設計。
3.圖形功能
MATLAB提供了兩個層次的圖形命令:一種是對圖形句柄進行的低級圖形命令,另一種是建立在低級圖形命令之上的高級圖形命令。利用MATLAB的高級圖形命令可以輕而易舉地繪制二維、三維乃至四維圖形,并可進行圖形和坐標的標識、視角和光照設計、色彩精細控制等等。
4.應用工具箱
基本部分和各種可選的工具箱。基本部分中有數百個內部函數。其工具箱分為兩大類:功能性工具箱和學科性工具箱。功能性工具箱主要用來擴充其符號計算功能、可視建模仿真功能及文字處理功能等。學科性工具箱專業性比較強,如控制系統工具箱、信號處理工具箱、神經網絡工具箱、最優化工具箱、金融工具箱等,用戶可以直接利用這些工具箱進行相關領域的科學研究。
MATLAB與通信仿真
一般來說,通信電路與系統仿真過程可以分為五個步驟:
1.系統建模:根據要分析的通信電路與系統,建立相應的數學模型。
2.仿真算法:找到合適的仿真算法。 MATLAB已經被確認為準確、可靠的科學計算標準軟件。
3.仿真語言:應用仿真語言編寫計算程序。MATLAB語言有非常突出的優點,是通信電路與系統仿真首選的仿真語言。
4.仿真計算:根據初步的仿真結果對該數學模型進行驗證。
5.系統仿真:進行系統仿真,并認真地分析仿真的結果。
仿真算法、仿真語言和仿真程序構成了數字仿真軟件。數學模型的正確性、仿真算法的可行性、仿真程序的準確性和可靠性,最后編制成一個成熟的仿真軟件。
通信電路與系統仿真在教學實踐中應用越來越普遍。對于改進教學效果、給學生提供形象化的信息、激發學生的學習興趣、提高學生的自學能力、加強學生對授課內容的理解等無疑是十分有益的。有利于對學生分析問題的能力和解決問題的能力的培養。
4.2 模擬調制信號的實現
軟件無線電具有靈活性,可擴展性等主要特點,這主要是因為軟件無線電的所有功能都是由軟件來實現(定義)的,通過軟件的增加,修改或者升級就可以實現新的功能。可以說,功能的軟件化是軟件無線電的最大優勢之一。在所有的軟件中,數字信號處理軟件占據著重要的位子,如:調制,解調,編碼,譯碼,信號識別,同步提取等都可以采用信號處理算法來實現。
4.2.1 AM信號調制算法與實現
AM波是怎樣的波?前面已經簡單提到,用期望信號去調制一個等幅信號的振幅的過程叫調幅,調制后的波就叫調幅波(AM波),這個被調制的信號叫載波。
設正弦型載波為:
(4.1)
式中:載波角頻率為 ;載波的初相位為 ;載波振幅為 。幅度調制信號的一般表達式為
(4.2)
其中A0=20,A1=5,A2=5,A3=5;
fc=10000Hz;fm1=1000Hz;fm2=2000 Hz;fm3=3000 Hz;
最后得到AM信號的時域表達式:
(4.3)
圖4.1 AM信號時域及頻域圖
從圖4.1可以看出,AM波的振幅變化與音頻信號一致,其波形是上下對稱的。在圖4.1中,可以看出包含了3個部分,第1部分是原來的載波,頻率是fc,振幅還是A0,第2部分為比載波高一個音頻頻的波(fc+fm1,fc+fm2,fc+fm3),第3部分為比載波低一個音頻頻率的波(fc-fm1,fc-fm2,fc-fm3),這二個部分分別被稱為上側邊帶和下側邊帶(USB,LSB),從式(4.2)可以知道這二個邊帶波各含有一個音頻信號fm1,fm2,fm3,AM波中的這3個成分除了一個原載波是等幅波外,從式(4.2)中推斷,上下邊帶這二個波成分其實也是等幅波(假定音頻fm1,fm2,fm3此時為一固定頻率比如1KHZ,2KHZ,3KHZ的正弦波),在調幅指數m為1時振幅分別為載波振幅的一半(A/2),頻率分別為fc+fm1,fc+fm2,fc+fm3和fc-fm1,fc-fm2,fc-fm3,也就是說音頻信號fm1,fm2,fm3分別包含在這二個等幅波中。
4.2.2 DSB信號調制算法與實現
DSB信號是一種與AM信號差不多形式的信號,與AM信號相比,只是其中不含有直流分量,如圖4.3所示,其中 是理想帶通濾波器。
其時域表達式為:
(4.4)
調制信號為:
(4.5)
圖4.2 抑制載波雙邊帶調制(DSB-SC)信號
DSB信號產生原理方框圖如圖4.3所示,其中詳細介紹了DSB信號產生的過程。
圖4.3 DSB信號產生原理方框圖
從圖4.2可以看出,DSB-SC波的振幅變化與音頻信號一致,其波形是上下對稱的。在圖4.2中,可以看出包含了2個部分,第1部分為比載波高一個音頻頻的波(fc+fm1,fc+fm2,fc+fm3),第2部分為比載波低一個音頻頻率(fc-fm1,fc-fm2,fc-fm3) 的波,這二個部分分別被稱為上側邊帶和下側邊帶(USB,LSB),從式(4.2)可以知道這二個邊帶波各含有一個音頻信號fm1,fm2,fm3。
4.2.3 SSB信號調制算法與實現
采用下邊帶調制時的單邊帶信號時域表達式為
(4.6)
采用上邊帶調制時的單邊帶信號時域表達式為
(4.7)
圖4.4 SSB信號產生原理方框圖
產生上邊帶信號時:
(4.8)
產生下邊帶信號時:
(4.9)
SSB信號通過MATLAB信號仿真,產生如圖4.5,4.6所示的截圖:圖上方為時域部分,圖下方為頻域部分。其產生原理即由圖4.4所示的原理方框圖。
圖4.5 抑制載波單邊帶調制(SSB)信號(上邊帶)及頻譜
圖4.6 抑制載波單邊帶調制(SSB)信號(下邊帶)及頻譜
4.2.4 VSB信號調制算法與實現
殘留邊帶(VSB)調制是一種幅度調制法,它是在雙邊帶(DSB)調制的基礎上,通過設計適當的輸出濾波器,使信號一個邊帶的頻譜成分原則上保留,另一個邊帶頻譜成分只保留小部分(殘留)。所以說,殘留邊帶調制是介于單邊帶調制與抑制載波雙邊帶調制之間的一種調制方式該調制方法由于其傳輸帶寬介于DSB和單邊帶(SSB)之間,既比雙邊帶調制節省頻譜,又比單邊帶易于解調.殘留邊帶調制的另一優點是便于實現,對發射機功放的峰均比要求比較低,因此它在廣播、電視技術等許多領域得到了廣泛的應用,如美國ATSC數字電視地面傳輸采用的就是殘留邊帶調制方。
對于具有低頻即直流分量的調制信號,用濾波法實現單邊帶調制時所需要的過渡帶是無限陡的理想濾波器,在殘留邊帶調制中已不再需要,這就避免了實現上的困難。其代價是傳輸頻帶增寬了一些。
殘旁邊帶常被運用在電視信號的傳輸上, 因為VSB信號無SSB調變信號的低頻響應差的缺點,且無DSB-SC調變信號波的頻寬,更無AM調變信號消耗大功率的缺點。因此,對于視頻基帶訊號,既可節省邊帶的頻寬,又可簡化接收電路的成本, 故使用VSB調變就顯得十分重要。 討論殘邊帶調變作為前提時,讓我們來考慮雙邊帶與載波在一起的情形。 假設輸入的基頻信號為
(4.10)
載波信號為
(4.11)
DSB信號可表示為
(4.12)
圖4.7 殘留邊帶調制(VSB)的濾波法形成
用濾波法實現殘留邊帶調制的原理如圖4.6所示。圖中 為殘留邊帶濾波器,殘留部分上邊帶時濾波器的傳遞函數如圖4.7所示。由濾波法可知,殘留邊帶信號的頻譜為
(4.13)
其時域表達式為
(4.14)
由圖示的濾波器函數,可以知道,VSB信號的時域表達式為:
(4.15)
圖4.8 殘留部分上邊帶時的傳遞函數
圖4.9 濾波法產生殘留邊帶調制VSB信號及頻譜
4.3 模擬調制信號數字化解調方法與仿真
4.3.1 AM信號解調方法與仿真
標準調幅信號(AM)可以使用SSB解調方法來解調,但是在本地載頻不夠準確的情況下,存在的較大的載頻分量會導致令人生厭的差頻聲.所以用SSB方法解調AM信號不是一種可取的方法。
前面已經提到,將音頻信號調制到載波上去就可以達到發送聲音的目的,可是我們的最終目的是實現聲音的遠距離傳送,所以還必須在接收一側將已調制的信號解讀出來,這個解調的過程就叫檢波,過去的書里有個很形象的比喻:將書信綁在箭上射出去的過程叫調制和發射,找到箭后取下書信就叫接收和檢波。
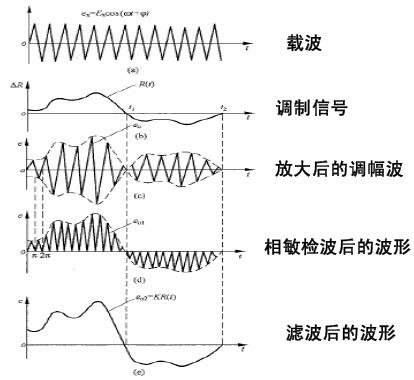
為了便于說明問題我們已經分析了AM信號的頻譜,實際的AM波形卻如圖4.10所示,是一個以載波為其頻率,振幅與音頻信號同步變化的上下對稱的波,也即其振幅變化的包絡就是我們需要的音頻信號,包絡檢波也得名于此,因為這個包絡是上下對稱互相抵消,為了得到它就必須將AM信號削去一半,這個目的可以通過使用具有單向導電特性的半導體二極管等整流元件來得到,只許AM信號的正半周或負半周通過,即可得到半個AM信號,再用電容等將細密振動的載波成分旁路吸收,最終得到音頻信號,完成整個檢波過程,因只使用簡單的二極管就能達到目的,所以一般收音機都采用這種檢波方式,不過這種檢波方式和下面即將介紹的同步檢波相比信號的再現性要低,因為檢出的是AM信號振幅變化的包絡,因受到干擾振幅變化的波形發生改變時,檢波得到的音頻信號也是受到干擾而改變的信號。
同步檢波是利用和載波同步的信號進行檢波的方式。這里所說的同步信號是由AM信號接收端產生。同步檢波的流程整理后如圖4.10。圖中最后可以看到USB和 LSB所含的音頻信號被分別提取出來,嚴格的說本文所討論的AM同步檢波過程中檢出的是上下邊帶音頻信號之和(和頻)與音頻信號之差(差頻)。這個音頻信 號之差沒有干擾時為零(兩側邊帶所含音頻信號原本是相同的),在其后的處理過程中分別將這個和差信號相加減后就能得到我們需要的一側邊帶音頻信號。達到削 除鄰頻干擾的目的。值得一提的是,包絡檢波雖將AM信號削去一半,AM信號的頻譜卻沒有發生改變,仍由一個載波和二個邊帶波而成,這也從另一個角度說明為什么普通使用二極管的包絡檢波不能消除鄰頻干擾也不能解調出SSB信號,因為前面說過SSB信號是將AM信號頻譜中的載波成分和一側邊帶濾除后得到的,既然使用二極管檢 波后信號的頻譜沒有改變,邊帶還是原來的邊帶,當然就不可以解調SSB信號了。
在圖4.10所示同步檢波流程中有3個信號是關鍵的,第一當然就是我們需要接收的AM信號,即圖中的入力信號。第二是與所要接收AM信號的載波同步的同步信號,這里的同步指的是同頻同相。第三是將剛才的同步信號移相后得到的移相信號。其實同步檢波就是一種”乘法檢波”,用同步信號和移相信號分別與入力AM信號相乘就能得到AM信號中包含的二個音頻信號之和與差。
圖4.10 AM信號解調輸出比較
基于DFT的數字化解調輸出圖形如圖4.10所示,從圖中可以看出,輸出圖形相差不多,仿真實驗取得較好的結果。
4.3.2 DSB信號解調方法與仿真
由于DSB信號含有”反相點”,所以對其采樣后并不能通過基于DFT的數字化解調方案來進行。但是我們也可以提取他的”反相點”,在每個”反相點”出記錄,在抽樣之后進行DFT運算時,記得在”反相點”出去負號,這樣便可以求出其幅值。當然也可一加入強載波實現DSB信號的解調,具體原理如圖4.11所示:
圖4.11 DSB信號濾波解調原理方框圖
具體參數如下
fc = 10000; %載波頻率
fm1 = 1000; %信號頻率
fm2 = 2000;
fm3 = 3000;
A1 = 5; %信號幅度
A2 = 5;
A3 = 5;
f(t)=A1cos(2*pi*fm1*t)+A2cos(2*pi*fm2*t)+A3cos(2*pi*fm3*t);
%寫產生調制信號f(t),fs=50000Hz
c(t)=cos(2*pi*fc*t); %產生載波信號c(t),fc=10000Hz
x= s.*c ; %幅度調制
y= x.*c ; %解調,加入強載波
濾波器特性部分設計:
[N,wn] =buttord(0.64,0.85,2,30); %設計巴特沃思數字低通濾波器
[b,a]=butter(N,wn);
s1= filter(b,a,y); %濾波
圖4.12 低通濾波特性
圖4.13 DSB信號解調輸出
4.3.3 SSB信號解調方法與仿真
由于DSP硬件速度所限,單邊帶信號的數字解調不能簡單套用單邊帶模擬接收機中采用的傳統的邊帶濾波器和乘法器組成的相干解調器。我們通過靈活運用多速率信號處理理論、調制理論和數字濾波理論,提出一種新的、有效的SSB數字解調算法(以下邊帶LSB為例)。原理框圖如圖4.16所示,對應的解調輸出過程如圖4.17所示。如設載波信號為
(4.16)
調制單音信號為
(4.17)
則收到的LSB信號為
(4.18)
圖4.14 SSB調制解調算法的原理框圖
我們取A=A1=A2=A3=5,然后乘以強載波,則
(4.19)
乘以強載波的圖形如圖4.15的S(t)×c(t)所示,明顯看見包絡圖形。然后進行低通濾波,除去3000Hz以外的頻率分量。就可以得到原始信號。
圖4.15 SSB信號解調輸出過程圖
本文再提出另外一種SSB信號解調方法,只做理論分析,不進行仿真實驗,具體推到過程如下:SSB信號時域表達式可以表示為
(4.24)
式中,”+”是上邊帶,”-”是下邊帶, 是 的Hilbert變換。
對信號正交分解得: 同相分量: (4.25)
正交分量: (4.26)
無論上邊帶,下邊帶,同相分量輸出就是調制信號。下面介紹另外一種SSB解調方法。其解調原理方框圖如圖4.18所示,根據Hilbert變換的性質,在 ,( 為信號的載波頻率, 為調制信號的最大頻率分量)的條件下,有一下近似表達式:
(4.27)
(4.28)
因此,下邊帶信號S(n)的Hilbert變換為
(4.29)
按照圖4.16所示運算過程,有
圖4.16 SSB信號一種解調方法
(4.30)
所以,經上述算法運算就可解調出調制信號。
4.3.4 VSB信號解調方法與仿真
由于VSB信號有”反相點”,所以,基于DFT的數字化解調方案并不能對VSB信號進行解調,只能采取相應的強載波解調來實現。
解調器抗噪聲性能的模型
圖4.17 VSB信號解調方框圖
由于篇幅所限,本文僅僅仿真實現,具體推導過程略去。具體仿真程序見附錄。
圖4.18 VSB解調信號與原信號比較
第五章 總結與展望
5.1 方案設計優點與待改進之處
方案設計優點:
1.計算量減少
本文提出的基于DFT的AM信號數字化解調方法,省去了本地載波恢復,低通濾波和數據抽取,解調計算量大大減少,且計算機仿真得到解調增益可到到G=3,表明該方法的抗干擾性能比傳統的相干解調方法有所明顯改進,渴望能過在采用AM信號的軟件數字化接收機中得到應用。
2.解調失真度很小
要正確的完成對AM信號的解調,必須考慮輸出的失真度。只有失真度限制在一定范圍內,才能不失真的恢復原始調制信號(通常應小于0.1)。失真度的表達式如下:
(5.1)
其中Px表示諧波功率,Ps表示輸出功率。
在不存在定時誤差的情況下,失真度很小,通過計算得出 ,可以完全忽略不計,改變調幅系數對解調輸出失真沒有明顯影響。
在存在定時誤差時,會對失真度有一定的影響。所謂定時誤差是值由于AM信號載波頻率設計值(或接收端對載波頻率測量存在誤差)和采樣定時精度有限等原因,使得對AM信號在一個載波周期內的平均采樣點數不是整數。若對AM信號每20個載波周期采樣159.5點(定時誤差大約為0.0031)使得失真度D=0.0081,每20個載波周期采樣159點,得到D=0.02。課件定時誤差會使失真度增大,但在通常的定時誤差條件下,失真仍然是可以忽略的。
3.抗干擾性能得到很大提高
在實際的通信信道中難免存在噪聲的干擾,對Am信號的解調抗干擾性能主要通過信噪比增益來體現。在基于DFT的AM信號數字化解調算法中,一方面由于DFT運算對噪聲有一定的濾波作用,另一方面,信號與噪聲是矢量相加的。所以噪聲對解調輸出的影響小了,而在相干解調方法中,信號與噪聲是獨立的,所以該方法的抗干擾性能要比傳統的相干解調有所改善。
對于上述解調方法的正確性和抗干擾性能,使用MATLAB語言編程進行了軟件仿真研究。取基帶信號頻率為f=1KHz的余弦波,載波頻率fc=10kHz,調幅系數為0.5,采樣頻率為100kHz,即每個載波周期采樣8個點,為了便于與傳統的相干解調比較,以下吧輸入信噪比定為輸入信號邊帶功率和輸入噪聲功率之比。
基于DFT的多音調制方案具有一個弱點,即各子信道之間存在著較大的頻譜重疊,導致了子信道之間的功率泄漏,從而引起了嚴重的串擾。對于碼間干擾和窄帶干擾嚴重的信道,子信道之間在頻譜上的分隔特性的好壞直接影響了整個多音調制系統的性能。針對這一問題,Sandberg和Tzannes等人設計了一種交迭離散多音調制系統 (Overlapped Discrete Multitone Modulation),也稱離散小波多音調制系統。此系統利用快速小波變換及其逆變換IFWT對信號進行分解與合成,其中FWT/IFWT是用余弦調制濾波器組實現的,在同樣的子通道數目下,這種濾波器頻譜響應的主瓣高出最大旁瓣45dB,而DFT只能獲得13dB的主/副瓣增益,從而大大改善了各子通道之間的頻譜分隔特性,同時仍然保證了各濾波器之間的正交特性。DWMT系統在ISI嚴重的情況下仍然具有較好的魯棒性,并且它不需采用DFT多音調制系統中的周期擴展就可獲得令人滿意的傳輸性能。
5.2總結
數字化解調算法在軟件無線電中的各種信號處理算法中占有極其重要的地位,甚至在一定程度上對DSP的性能提出了要求,而對于目前A/D轉換器、DSP芯片等器件的性能還不能滿足軟件無線電需要的狀況,如果能開發出計算量小,容易實現而又具有好的解調性能的解調算法就更能顯出其優越性了。本文主要是對軟件無線電中的數字化解調方法進行研究,研究中所完成的主要研究成果如下:
1.通過總結分析現有的數字化解調方法,指出對AM信號的數字化解調方法只是對傳統的模擬電路中解調方法的數字化實現,沒有結合軟件無線電的特點進行優化。對少數采用DFT變換實現AM,DSB信號的數字化解調方法進行深入的研究,并將其思想引入到AM信號的解調中,從而提出了一種適用于軟件無線電的基于DFT的AM信號數字化解調方法。
2.該方法不僅具有DFT算法的優越性,即省去了以往解調方法中的載波同步和兩路低通濾波,從而大大降低了計算量,簡化了解調過程。
3.采用MATLAB語言對整個解調過程進行了仿真研究。仿真過程中所得到的AM波形和載波周期幅值都與作者的分析一致,證明了該方法的可行性。仿真最終得到的結果信噪比曲線圖也證實了該方法的抗干擾性能比傳統的相干解調算法有所改善。整個仿真過程的實現對于解決軟件無線電系統的仿真問題也有一定的參考價值。
4.對該解調方案基于軟件無線電的實現給出了設計方案。
5.3 收獲與心得
作者在本文中提出的基于DFT的數字化解調方法對于AM信號而言,比以往所采用的相干解調以及數字化正交解調有所改善,但只是對眾多調制方式中的一類信號的解調方法而言,還遠遠不能滿足軟件無線電對各種調制信號的解調需要。但是,這種解調方法的思想對軟件無線電中的數字化解調算法卻有著一定的啟發作用:既然可以通過DFT提取信號的幅度信息來解調AM信號,那么對于幅度與相位相結合的正交幅度調制信號(MQAM)是否也可以采取這種方法來解調呢?作者認為理論上是完全可行的。因為MQAM信號的解調恢復是靠提取出其中的幅度和相位信息,而DFT完全可以做到,只是在對AM信號的解調中,提取出的幅度信息是用于建立位同步的。采用DFT實現對MQAM信號解調的可行性和解調性能還需要通過具體的仿真實驗來驗證,這是有待于進一步研究的問題。
 電子發燒友App
電子發燒友App






















評論