圖來表示，就會很清楚的看到其中的耦合關(guān)系。 由永磁同步電機(jī)的電壓方程和數(shù)學(xué)模型可以看出，d軸電壓 Ud 不僅受 d軸電流 id 的影響，還受q軸電流 iq的影響，這說明永磁同步電機(jī) d軸電壓 和 q軸電壓 存在一種耦合關(guān)系。我們可以將公式中的? 和 視作耦合項(xiàng)，由于耦
2021-03-22 16:37:50
14084 
哪位大俠擅長做matlab數(shù)值計(jì)算，主要是微分方程組的求解，可以盡快聯(lián)系我，必有重謝。qq631467039
2013-02-26 17:03:20
微分方程經(jīng)典求解法 一個線性系統(tǒng)，其激勵信號 &
2009-09-10 12:23:18
計(jì)算：自然數(shù)n的階乘; n中取m的組合數(shù); 已知兩個多項(xiàng)式(不一定同階)的系數(shù)，求這兩個多項(xiàng)式的和。實(shí)驗(yàn)二⒈實(shí)驗(yàn)?zāi)康呐c要求通過對具體實(shí)例的分析，學(xué)會運(yùn)用微分方程、變分法等數(shù)學(xué)方法建立確定性連續(xù)模型
2008-09-24 11:33:07
系統(tǒng)辨識數(shù)學(xué)模型及常用輸入信號.ppt
2017-08-13 15:53:07
1. A、B、C三相坐標(biāo)系中PMSM數(shù)學(xué)模型定子電壓方程：結(jié)論：在A、B、C坐標(biāo)系下，可以看出電壓方程和磁鏈方程比較復(fù)雜，磁鏈的數(shù)值隨永磁同步電機(jī)定轉(zhuǎn)子之間的相對位置隨時間而變化，而電機(jī)運(yùn)動方程
2021-08-27 07:59:14
Matlab偏微分方程工具箱應(yīng)用說明1． 概述本文只給出該工具箱的函數(shù)列表，讀者應(yīng)先具備偏微分方程的基本知識，然后根據(jù)本文列出的函數(shù)查閱Matlab的幫助，便可掌握該工具箱的使用。2． 偏微分方程
2009-09-22 15:26:19
本帖最后由 A670521546 于 2011-7-8 10:29 編輯
常微分方程(ODEs)的MATLAB數(shù)值解法》偏微分方程(PDEs)的MATLAB數(shù)值解法》Z變換和差分方程
2011-07-08 08:42:45
三相永磁同步電機(jī)的矢量控制一 內(nèi)容三相永磁同步電機(jī)CPMSM）是一個強(qiáng)搞合、復(fù)雜的非線性系統(tǒng)，為了能夠更好地 設(shè)計(jì)先進(jìn)的 PMSM 矢量控制算法，建立合適的數(shù)學(xué)模型就顯得尤為重要。本次學(xué)習(xí)PMSM
2021-08-27 07:02:16
Pmsm在旋轉(zhuǎn)坐標(biāo)系的數(shù)學(xué)模型坐標(biāo)變換dq軸電壓方程整體模型電壓計(jì)算模塊dq軸磁鏈計(jì)算d,q軸電流轉(zhuǎn)距計(jì)算轉(zhuǎn)速計(jì)算仿真結(jié)果因?yàn)檗D(zhuǎn)動慣量較小，轉(zhuǎn)速迅速跟隨同步轉(zhuǎn)速順利啟動。A相電流與電壓波形...
2021-08-27 07:56:09
字有點(diǎn)丑，不知道大家能不能看清。我把我的問題簡化了一下，本來是一個求解簡單的微分方程組的問題，如果方程中的u在10s內(nèi)只有一組數(shù)據(jù)，這個問題我找到了求解方法。但是這個問題的關(guān)鍵在于在這10s內(nèi)我們
2018-08-23 16:30:37
... 902.3.1 一元函數(shù)的數(shù)值積分... 902.3.2 二元函數(shù)重積分的數(shù)值計(jì)算... 922.4 常微分方程數(shù)值解
2008-06-18 13:50:11
理解常微分方程單步法與多步法思想，掌握常用算法的設(shè)計(jì)，掌握用MATLAB實(shí)現(xiàn)的數(shù)值解法。利用MATLAB中數(shù)值解法“”求解，并用圖形表示各種方法的精度。利用常微分解法可知方程的解為：for i=2
2011-11-03 15:36:59
、磁鏈方程、轉(zhuǎn)矩方程和運(yùn)動方程四大方程之間的變量關(guān)系復(fù)雜，其數(shù)學(xué)模型是一個比較復(fù)雜且強(qiáng)耦合的多變量系統(tǒng)，所以使用坐標(biāo)變換的方法對其進(jìn)行降階和解耦，以方便設(shè)計(jì)控制器對電機(jī)進(jìn)行控制。三相永磁同步電機(jī)
2018-09-16 13:02:18
如圖是一個簡單的RL串聯(lián)電路，假設(shè)知曉U R iL和L的值，可以列出以下微分方程。如果方程等式正確的話，請問要如何繼續(xù)的出i(t)的等式呢？
2019-01-08 11:55:32
什么是數(shù)學(xué)建模,怎樣建立數(shù)學(xué)模型
2009-09-15 12:53:30
d2y/dx^2=-1001dy/dx-1000y 數(shù)值方法求解此微分方程式,x=0到5.使用h=0.5和隱性的方式 。起始條件y(0)=1和y`(0)=0以圖形顯示這兩個結(jié)果并比較差異。求高人！感激不盡！
2013-01-10 00:52:16
的分母為系統(tǒng)的特征多項(xiàng)式；極點(diǎn)：特征多項(xiàng)式等于0組成特征方程的根；階數(shù)：特征多項(xiàng)式的最高階數(shù)n；根軌跡增益：；拉普拉斯變換：可采用傳遞函數(shù)代替常系數(shù)微分方程來描述系統(tǒng)的特性。這就為采用直觀和簡便的圖解方法來確定控制系統(tǒng)的整個特性、分析控制系統(tǒng)的運(yùn)動過程，以及提供控制系統(tǒng)調(diào)整的可能性。
2019-05-21 08:43:40
隨時間變化。 若溫度也隨時間變化，那么方程式成為。。。？（方程式iv）？。。。我們就此不考慮這些方程式的推導(dǎo)，但若您感興趣您將在我們的“工程師和科學(xué)家的數(shù)學(xué)”第二卷中找到一定數(shù)量的偏微分方程的推導(dǎo)
2020-08-29 14:31:01
該仿真模型的主要目標(biāo)是建立光伏系統(tǒng)的數(shù)學(xué)模型，然后利用MPPT控制器進(jìn)行MATLAB仿真，以達(dá)到最大發(fā)電量。The main objective of this simulation model
2021-11-15 08:51:14
1.同步旋轉(zhuǎn)坐標(biāo)系下的數(shù)學(xué)模型1.1 dq坐標(biāo)系下的定子電壓方程1.2 dq坐標(biāo)系下的定子磁鏈方程1.3 定子電壓方程變換式及等效電路由上述兩個方程，可以得到定子電壓方程的新等式：電壓等效電路如下
2021-09-03 07:20:48
永磁同步電機(jī)最大的優(yōu)勢在于其簡單的結(jié)構(gòu)，低廉的生產(chǎn)成本以及穩(wěn)定的運(yùn)行狀態(tài)。本文的主要研究工作基于相坐標(biāo)系，建立永磁同步發(fā)電機(jī)定子繞組匝間短路、轉(zhuǎn)子磁場損失的數(shù)學(xué)模型，通過這些MATLAB程序，對系統(tǒng)
2021-08-27 06:15:52
本帖最后由 narushin 于 2019-9-9 09:34 編輯
研究生剛?cè)雽W(xué)，跟著一個師兄在做多電機(jī)智能控制，他讓我寫多電機(jī)的數(shù)學(xué)模型。建立多電機(jī)系統(tǒng)的目的是實(shí)現(xiàn)多電機(jī)的同步智能控制，當(dāng)
2019-09-09 08:48:49
如何列寫控制系統(tǒng)微分方程？列寫控制系統(tǒng)微分方程注意事項(xiàng)有哪些？
2021-10-25 06:12:49
...PAGE...目錄 TOC \o "1-3" \h \z \u1 引言 12 異步電動機(jī)動態(tài)數(shù)學(xué)模型 22.1異步電動機(jī)動態(tài)數(shù)學(xué)模型的性質(zhì) 22.2三相異步電動機(jī)的多變量非線性數(shù)學(xué)模型 22.2.1電壓方程 32.2.2磁鏈方程 42....
2021-09-03 06:54:40
請教各位牛人，小女子初學(xué)matlab，現(xiàn)遇到如下問題，還請各位多多指教，具體問題如下：有一個時滯微分方程如圖所示： 現(xiàn)在需要時間延遲tau不停變化，從0到20，從而畫出x抽為tau，y軸分別為S,L
2015-10-29 22:38:32
直流電動機(jī)系統(tǒng)中的字母符號有何含義？怎樣去搭建一種直流電動機(jī)系統(tǒng)的數(shù)學(xué)模型？如何對直流電動機(jī)系統(tǒng)的數(shù)學(xué)模型進(jìn)行仿真？
2021-07-30 07:51:04
各位朋友，本人現(xiàn)在正在搭建雙饋異步電機(jī)的內(nèi)部模型，但是要和外部的電氣模型連接起來，不知道怎樣把數(shù)學(xué)模型封裝成電氣模型啊，在MATLAB中，有個三相異步電機(jī)的原始電氣模型，打開里面的建模，是將數(shù)學(xué)模型封裝成電氣模型的，但是卻看不到是如何封裝的，希望各位多多幫忙啊，大家可以交流下！
2012-12-13 21:37:21
第二章 控制系統(tǒng)的數(shù)學(xué)模型2-1 引言2-2 微分方程的建立及線性化
2009-05-26 15:29:42
控制模型。1，數(shù)學(xué)模型??通過很多書籍，我們都可以找到電機(jī)在選擇坐標(biāo)系dq下的數(shù)學(xué)模型，其中定子電壓方程如下：??其中usd、usq分別為定子電壓的d-q軸分量；isd、isq分別是定子電流的...
2021-06-28 10:08:45
永磁同步電機(jī)電機(jī)本體數(shù)學(xué)模型在MATLAB下的仿真永磁同步電機(jī)電機(jī)本體數(shù)學(xué)模型在MATLAB下的仿真張紅生，等永磁同步電機(jī)電機(jī)本體數(shù)學(xué)模型在MATLAB下的仿真張紅生，吳炳嬌(蘭州交通大學(xué)自動化
2021-08-27 07:33:06
用LabVIEW解常系數(shù)微分方程：K*S=dN/dt K為常數(shù)，S為程序輸入量，N為輸出量，t為時間求大神解
2016-04-08 17:27:52
本帖最后由 映月2016 于 2022-1-4 13:57 編輯
求解微分方程，x的范圍0≤x≤30在哪里設(shè)置？
2022-01-04 11:30:22
要進(jìn)一步研究一個自動控制系統(tǒng)， 就需要建立系統(tǒng)的數(shù)學(xué)模型來描述一個系統(tǒng)。 所謂數(shù)學(xué)模型， 就是描述系統(tǒng)輸入、 輸出變量以及內(nèi)部各變量之間關(guān)系的數(shù)學(xué)表達(dá)式。 常用微分方程來描述系統(tǒng)各變量的動態(tài)關(guān)系
2021-09-15 07:20:21
這個是微分方程組，wind和wave都是隨時間變化的外載，他們是一串excel數(shù)據(jù)，如圖所示，請大神解答。以前第一次發(fā)，忘記上圖了，今天特意重發(fā)一下。希望有網(wǎng)上的大神幫忙，謝謝
2018-08-20 19:42:12
第4章交流同步電機(jī)的數(shù)學(xué)模型
2020-04-02 11:35:00
） 1------------------------------------為了演示拉普拉斯變換的用途以及在系統(tǒng)分析中包含的步驟， 再次思考彈簧-質(zhì)量-阻尼系統(tǒng)如方程（2.1）所描述，即。。。？Mdyt（二次微分方程）.?。。。（2.18）我們希望獲得
2020-08-14 20:38:00
這里開始要講講三相異步電機(jī)（鼠籠電機(jī)）的數(shù)學(xué)模型如之前講過的，當(dāng)定子同上三相交流電后，產(chǎn)生定子電流，電子電流產(chǎn)生磁場，根據(jù)電機(jī)等效電路模型，可以得出轉(zhuǎn)子也產(chǎn)生感應(yīng)電壓，因?yàn)檗D(zhuǎn)子線圈閉合，產(chǎn)生轉(zhuǎn)子電流
2021-09-06 07:37:56
手中有微分方程，想用電路實(shí)現(xiàn)它。初次接觸，不知道從什么地方下手。希望大神指點(diǎn)一下，應(yīng)該學(xué)些什么？
2018-04-04 22:39:56
想用laabveiw解微分方程組，有大神會做嗎
2018-08-16 09:25:20
模糊PID控制方式與傳統(tǒng)PID控制相比有何優(yōu)勢？怎樣去搭建一種模糊控制器系統(tǒng)的數(shù)學(xué)模型？如何對模糊控制器系統(tǒng)的數(shù)學(xué)模型進(jìn)行仿真？
2021-08-18 07:35:38
一、邊緣檢測邊緣檢測的幾種微分算子：一階微分算子：Roberts、Sobel、Prewitt二階微分算子：Laplacian、Log/Marr非微分算子：Canny一階微分算子1.Roberts
2021-07-26 08:29:56
運(yùn)行特性和數(shù)學(xué)模型
2013-04-10 21:35:00
這個微分方程組能使用數(shù)值積分求解嗎？如果能使用什么方法求解呢？m和F都是已知的，泣血跪求大神解答啊
2014-08-08 14:35:23
【全美經(jīng)典】微分方程 第二版
2008-08-08 14:57:11
0 控制系統(tǒng)的數(shù)學(xué)模型:系統(tǒng)微分方程的建立方法 Laplace變換的定義及性質(zhì) 傳遞函數(shù)的定義及性質(zhì) 控制系統(tǒng)中的典型環(huán)節(jié)及傳遞函數(shù)的數(shù)學(xué)模型 動態(tài)結(jié)構(gòu)
2009-01-08 13:56:285 摘要:對一些不能求解解析解的常微分方程和偏微分方程進(jìn)行精確求解是非常困難的，探討了用MATLAB方法對此類方程進(jìn)行求解，結(jié)合實(shí)例介紹了MATLAB數(shù)值計(jì)算的方法，先將物體的運(yùn)
2009-01-08 21:24:3761 研究了一類含有“一般”時延的高階泛函微分方程的周期解問題，將原方程化為等價的泛函微分方程，并利用該等價泛函微分方程的特征方程，得到了原方程具有周期解的充分必
2009-02-28 17:07:1115 常微分方程復(fù)習(xí),常微分方程pdf：微分方程的一般概念線性常微分方程的性質(zhì)一階線性常微分方程二階線性常系數(shù)微分方程二階線性變系數(shù)微分方程
2009-04-23 22:08:330 導(dǎo)熱微分方程式視頻教程
2009-07-05 19:28:1537 物理系統(tǒng)的數(shù)學(xué)模型 §2.1 引言 §2.2 元件和系統(tǒng)運(yùn)動方程的建立 §2.3 運(yùn)動方程的線性化 §2.4 控制系統(tǒng)的元件
2009-07-11 08:41:080 系統(tǒng)模型及其分類系統(tǒng)：具有特定功能的總體，可以看作信號的變換 器、處理器。系統(tǒng)模型：系統(tǒng)物理特性的數(shù)學(xué)抽象，一般也稱為數(shù)學(xué)模型。 電路的微分方程為:該微
2009-09-08 21:00:2510 最佳捕魚策略的數(shù)學(xué)模型本文的數(shù)學(xué)模型提法清楚，相對于捕撈強(qiáng)度遞增的不同預(yù)測值，對魚群變化進(jìn)行動態(tài)模撥。
2009-09-16 11:37:32113 微分方程式的建立與求解:復(fù)習(xí)求解系統(tǒng)微分方程的經(jīng)典法物理系統(tǒng)的模型微分方程的列寫n 階線性時不變系統(tǒng)的描述求解系統(tǒng)微分方程的經(jīng)典法一．物理系統(tǒng)的模型
2009-09-30 19:30:070 對于高階線性微分方程，各教材均有系統(tǒng)的求解方法 ．而對于一般高階非線性微分程，由于沒有系統(tǒng)的解法，故有關(guān)微分方程的專門教材也未給與更多的介紹．而僅僅對一些較為特
2010-03-03 22:12:5224 摘 要：研究了一類多時滯拋物型微分方程組解的振動性質(zhì)，利用一階脈沖微分不等式獲得該類方程組在兩類齊次邊界條件下判別其若干解振動的充分條件．關(guān)鍵詞：多時滯；脈
2010-03-03 22:14:136 摘要：提出在高階電路中運(yùn)用狀態(tài)方程求解各個變量的具體方法和步驟，以便于應(yīng)用計(jì)算機(jī)分析電路。其優(yōu)點(diǎn)是比求解高階微分方程要容易得多， 尤其是用數(shù)值法在計(jì)算機(jī)上求解時
2010-04-29 08:53:2720 本章概述2.1 動態(tài)微分方程式的編寫2.2 傳遞函數(shù)2.3 典型環(huán)節(jié)的傳遞函數(shù)2.4 系統(tǒng)動態(tài)結(jié)構(gòu)圖2.5 系統(tǒng)結(jié)構(gòu)圖等效變換和化簡2.6 系統(tǒng)傳遞函數(shù)的求取
2010-08-20 16:22:0963 微分、積分和微分方程4.1. 知識要點(diǎn)和背景：微積分學(xué)基本定理 4.2 實(shí)驗(yàn)與觀察（Ⅰ）：數(shù)值微積分4.2.1實(shí)驗(yàn)：積分定義、微分
2008-10-17 00:32:434430
2-2 系統(tǒng)微分方程的解——系統(tǒng)的全響應(yīng)
一、 線性系統(tǒng)微分方程線性的證明
線性系統(tǒng)必須同時滿足齊次性與疊加性。所以，要證明線性系統(tǒng)
2009-07-09 09:45:314099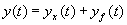 
控制系統(tǒng)的數(shù)學(xué)模型
傳遞函數(shù)
方塊圖表示的模型
2009-07-27 14:06:384227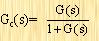 
在生產(chǎn)和科學(xué)實(shí)驗(yàn)中，選取的數(shù)學(xué)模型主要是線性回歸方程形式，采用回歸分析方法確定模型的參數(shù)。由于BP 網(wǎng)絡(luò)可對任意形狀的函數(shù)曲線進(jìn)行逼近，因此，采用BP 網(wǎng)絡(luò)建立的數(shù)學(xué)模型
2011-05-14 16:35:5623 電子發(fā)燒友網(wǎng)站提供《[全美經(jīng)典學(xué)習(xí)指導(dǎo)系列] 微分方程(第二版).txt》資料免費(fèi)下載
2012-09-29 16:23:330 該文檔是課本《常微分方程》（王高雄，第三版）的課后答案，里面詳細(xì)寫出了《常微分方程》（王高雄，第三版）課后習(xí)題答案。
2016-03-04 15:58:290 第2章 系統(tǒng)辨識數(shù)學(xué)模型及常用輸入信號
2017-06-12 09:53:508 并討論了分?jǐn)?shù)階偏微分方程在圖像去噪和圖像超分辨率重建中的相關(guān)理論與模型；通過仿真實(shí)驗(yàn)表明，基于分?jǐn)?shù)階偏微分方程的方法在去噪和減少階梯效應(yīng)等方面比整數(shù)階偏微分方程更具有優(yōu)勢；最后指出了未來的相關(guān)研究問題。
2017-12-06 10:50:041 針對增強(qiáng)圖像中的弱邊緣、細(xì)節(jié)紋理和消除二階偏微分方程在圖像平滑部分的階梯效應(yīng)問題，提出一種各向異性四階偏微分方程耦合二階偏微分方程的圖像放大算法。算法通過像素的局部方差自適應(yīng)約束閾值，實(shí)現(xiàn)圖像
2018-01-12 14:38:170 Hinton創(chuàng)建的向量學(xué)院的研究者提出了一類新的神經(jīng)網(wǎng)絡(luò)模型，神經(jīng)常微分方程（Neural ODE），將神經(jīng)網(wǎng)絡(luò)與常微分方程結(jié)合在一起，用ODE來做預(yù)測。
2018-06-26 11:19:1110805 Logistic分?jǐn)?shù)階微分方程并應(yīng)用提出的離散化方法對模型進(jìn)行數(shù)值求解;然后，根據(jù)不動點(diǎn)理論討論該合成動力系統(tǒng)不動點(diǎn)的穩(wěn)定性，給出了在參數(shù)空間內(nèi)二維Logistic 分?jǐn)?shù)階系統(tǒng)發(fā)生第一次分岔的邊界方程;最后，借助Matlab對模型進(jìn)行數(shù)值仿真，并結(jié)合Lyapunov指數(shù)、相圖
2019-05-17 16:38:465 研究人員已經(jīng)開始探索使用ML在高性能計(jì)算方面提供持續(xù)改進(jìn)的可能，以解決偏微分方程和科學(xué)計(jì)算中的困難計(jì)算問題。
2019-07-30 10:20:523206 對于復(fù)雜的微分方程模型的求解， 可以借助 MATLAB 偏微分方程工具箱中的專用求解器。以下將以一個實(shí)例來看看如何借助偏微分方程工具箱來實(shí)現(xiàn)一個微分方程的求解與數(shù)值仿真。
2019-09-16 11:41:373369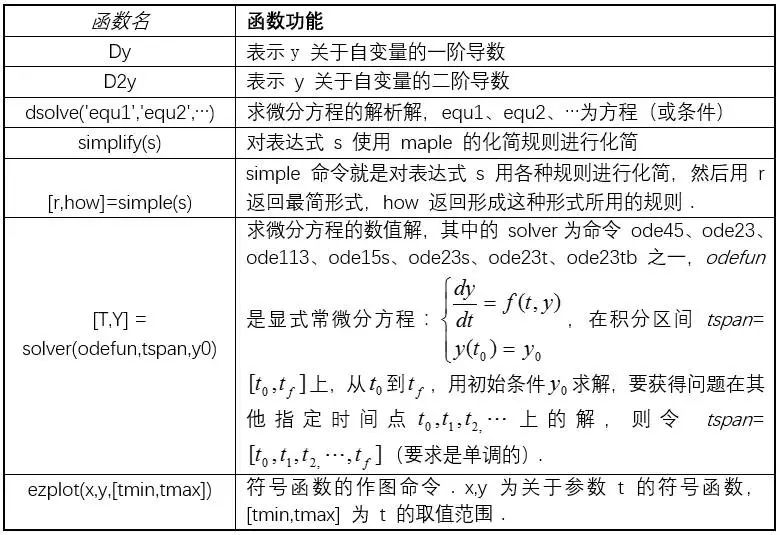 
系統(tǒng)的數(shù)學(xué)模型是描述系統(tǒng)輸入、輸出變量以及內(nèi)部各個變量之間關(guān)系的數(shù)學(xué)表達(dá)式。
2019-09-06 08:00:000 分?jǐn)?shù)階微積分理論是整數(shù)階微積分理論的推廣，發(fā)展至今已有300多年的歷史。特別是近幾十年來，分?jǐn)?shù)階微分方程在物理、化學(xué)、生物、金融數(shù)學(xué)等不同的學(xué)科領(lǐng)域已得到廣泛的應(yīng)用。具p-Laplace算子
2019-12-05 15:53:003 Logistic分?jǐn)?shù)階微分方程并應(yīng)用提出的離散化方法對模型進(jìn)行數(shù)值求解；然后，根據(jù)不動點(diǎn)理論討論該合成動力系統(tǒng)不動點(diǎn)的穩(wěn)定性，給出了在參數(shù)空間內(nèi)二維Logistic分?jǐn)?shù)階系統(tǒng)發(fā)生第一次分岔的邊界方程；最后，借助Matlab對模型進(jìn)行數(shù)值仿真，并結(jié)合Lyapunov指數(shù)、相圖
2019-12-12 15:45:3415 本文檔的主要內(nèi)容詳細(xì)介紹的是自動控制系統(tǒng)的數(shù)學(xué)模型的學(xué)習(xí)教程包括了：控制系統(tǒng)微分方程的建立，傳遞函數(shù)，動態(tài)結(jié)構(gòu)圖，典型反饋系統(tǒng)的幾種傳遞函數(shù)
2020-01-07 17:22:376 拉氏變換法和算子符號法在求解微分方程時的區(qū)別和聯(lián)系？
2020-04-14 08:00:005 Logistic分?jǐn)?shù)階微分方程并應(yīng)用提出的離散化方法對模型進(jìn)行數(shù)值求解;然后，根據(jù)不動點(diǎn)理論討論該合成動力系統(tǒng)不動點(diǎn)的穩(wěn)定性，給出了在參數(shù)空間內(nèi)二維Logistic分?jǐn)?shù)階系統(tǒng)發(fā)生第一次分岔的邊界方程;最后，借助Matlab對模型進(jìn)行數(shù)值仿真，并結(jié)合Lyapunov指數(shù)、相圖、時
2021-03-30 09:32:3910 電機(jī)的數(shù)學(xué)模型與仿真分析。
2021-05-19 14:56:5720 一、什么是微分算子符號？ 描述線性系統(tǒng)的激勵函數(shù)和響應(yīng)函數(shù)間關(guān)系的微分方程，具有以下形式： 式中 為時域中的微分算子符號，當(dāng)它們作用于某一時間函數(shù)時，該函數(shù)就要對時間變量t分別進(jìn)行一次和n此微分
2021-05-20 15:06:308793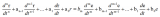 
具ρLaplace算子的分?jǐn)?shù)階微分方程邊值問題解的存在性(深圳核達(dá)中遠(yuǎn)通電源技術(shù)有限公司待遇怎么樣?)-第一章介紹有關(guān)分?jǐn)?shù)階微積分理論的研究背景、發(fā)展歷史及研究現(xiàn)狀，具p-Laplace算子的分?jǐn)?shù)
2021-09-17 13:38:095 主要介紹了用matlab方法求解初值問題和邊值問題的常微分方程采用四階龍格庫塔法和歐拉法，含matlab代碼
2021-12-30 11:01:250 控制系統(tǒng)微分方程是在時間域描述系統(tǒng)動態(tài)性能的數(shù)學(xué)模型，在給定外作用及初始條件下，求解微分方程可以得到系統(tǒng)的輸出響應(yīng)。
2023-03-09 16:49:532821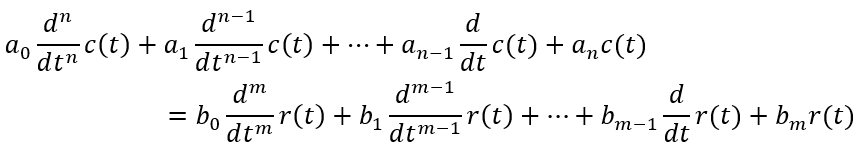 
同步電機(jī)的數(shù)學(xué)模型包括什么呢？
電壓方程、磁鏈方程、轉(zhuǎn)矩方程等等。
大家都知道永磁電機(jī)是一個非線性的系統(tǒng)；
各種變量參數(shù)之間的關(guān)系及其相應(yīng)的計(jì)算也較為復(fù)雜，
因此，通過對坐標(biāo)進(jìn)行變換，從而保證坐標(biāo)變換前后電流矢量的不變，
2023-03-14 13:54:501 這一次日篤小編來教大家如何在simulnk里面，求解偏微分方程（Partial Differential Equation-PDE）。
2023-06-25 16:03:171484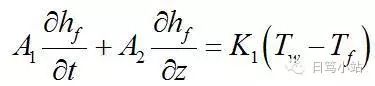 
微分代數(shù)方程是一類微分方程，其中一個或多個因變量導(dǎo)數(shù)未出現(xiàn)在方程中。
2023-07-19 11:15:421054 
系統(tǒng)數(shù)學(xué)模型時域表示：端口（輸入-輸出）描述（一元n階微分方程）與狀態(tài)方程描述（n元聯(lián)立一階微分方程）
2023-08-09 14:53:22742 
電子發(fā)燒友App
為激勵， 
， 
為響應(yīng)。對兩個網(wǎng)孔回路可列出KVL方程為
， 
的聯(lián)立微分積分方程。
，即
?，
，…， 
后，上述微分方程即可寫
? ，
?????????????? 
???????????? 
表示則為
? ???????????????????????? 
的傳輸算子及u1(t),u2(t)分別對i(t)的微分方程。
? 
???? 
??? 
??????????????????? 
????? 
都是相同的，
工商網(wǎng)監(jiān)
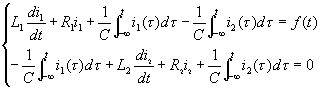
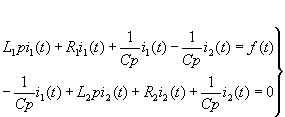
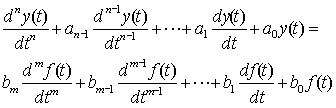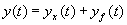
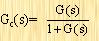
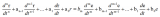
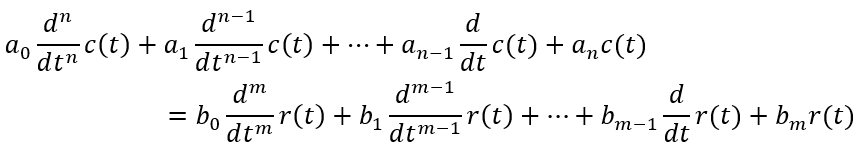
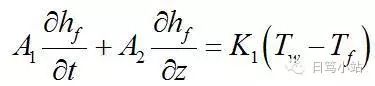
評論