通信系統不可避免地要受到各種干擾的影響,使接收端收到的信息與發送端發出的信息不一致,即接收端收到的信息產生了誤碼。為了降低數據通信線路傳輸的誤碼率,通常有改善數據通信線路傳輸質量和差錯檢測控制兩種方法。差錯檢測控制的方法很多,本文討論在10G以太網接人系統中并行實現CRC-32編解碼的方法、并行CRC算法的Unfolding算法可以實現并行CRC的計算,但是并行電路所用的資源增加到了原來的J倍。8位并行CRC算法、并行CRC-16的編碼邏輯、USB技術中并行CRC算法給出的并行算法都建立在公式遞推的基礎上。當并行深度較小時,遞推算法比較適用。而當并行深度很大的情況下(10G以太網接人系統使用64比特并行數據通路),遞推過程就顯得過于煩瑣而缺乏實用性。為此,本文提出了矩陣法、代入法和流水線法等三種算法,解決了深度并行情況下CRC算法的實現問題。利用本文提出的算法,可以得出64比特并行CRC計算的邏輯表達式,并用于10G以太網接入系統的設計。設M/(x)為信息多項式,G(x)為生成多項式。一般的CRC編碼方法是:先將信息碼多項式左移r位,即M(x)·xr,然后作模2除法
(M(x)· x r)/G(x)=Q(x)+R(x)/G(x) (1)
所得到的月(x)就是CRC校驗碼。以二進制碼0x9595H的CRC-32編碼為例:
· 將信息碼左移32比特變成0x959500000000H,記為m。
·CRC-32G的生成多項G(x)=x32+x26+x23+x22+x16+x12+xll+x10+x8+x7+x5+x4+x2+x+1,轉換成16進制碼為g=0x104C01DB7H。用m除以g(模2除法),所得余數0x3738F30BH就是0x9595H的CRC-32碼。實現0x9595H的基本CRC-32編碼的Matlab程序如下:
g(33:-1:1)=[1,0 0 0 0 0 1 0 0,1 1 0 0 0 0 0 1,0 0 0 1 1 1 0 1,1 0 1 1 0 1 1 1];
a(48:-1:1)=[1 0 0 1 0 1 0 1,1 0 0 1 0 1 0 1,0 0 0 0 0 0 0 0,0 0 0 0 0 0 0 0,0 0 0 0 0 0 0 0,0 0 0 0 0 0 0 0];
for i=48:-1:33,
if a(i)= =1
a(i:-1:i-32)=xor(a(i:-1:i-32),i(33:-1:1));
end
end
crc=a(32:-1:1)
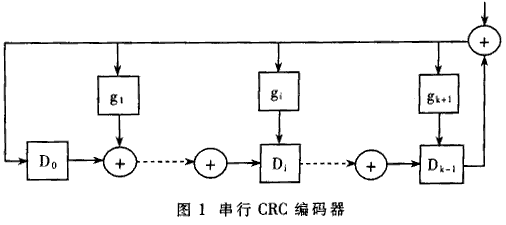
如果想用以上CRC-32程序計算其他長為L的序列的基本CRC-32碼,只需將數組α的上界和for循環中i的初始值改為32+L,并用該序列代替數組。開始的序列"1001010110010101"即可。用數字電路實現的串行CRC編碼器如圖1所示。圖1中每個矩形表示D觸發器。gi的取值范圍是1或者0。取1時表示通路,取0時表示斷路。進行基本CRC-32編碼時,每個D觸發器初始狀態為0,從數據端串行輸入二進制的信息碼。信息碼輸入結束后,D觸發器中鎖存的數值就是信息碼的基本CRC-32編碼。此電路適用于信息碼長為任意值的情況。在某些信息系統中以基本CRC產生算法為基礎附加了新的規定。例如IEEE802.3協議規定,以太網的FES(幀校驗序列)域以CRC-32為基礎,并且在編碼時首先將信息碼的最初4個字節取反碼,對目的地址、源地址、長度/類型域、數據域、PAD域求出基本CRC-32碼之后再將結果取反,最后的結果才是FCS。同上述過程等價的另一種實現方法是將圖1中所有D觸發器的初值置1,這樣結果不必取反。為使電路設計者驗證其FCS編碼正確,IEEE802.3還給出了一個樣本,即:將序列0xBED723476B8FB3145EFB3559H重復126次,最后得到的FCS值應該為0x94D254ACH。10G以太網是IEEE802.3ae工作組提出的建議。它保持了以前以太網的幀結構,但是線速度達到了10Gbps的量級。為了降低10G以太網接入系統的功耗并達到芯片加工工藝的要求,必須采用并行數據通路。為計算FCS需要研究并行CRC算法。所設計的10G以太網接入系統采用64比特并行數據通路,因此本文主要討論64比特并行CRC-32的實現方法。本文共介紹三種實現方法,其中矩陣法和代入法是基于組合邏輯的直接實現方法,第三種方法是基于流水線的實現方法。
1 矩陣法
記圖1中的32個D觸發器的輸出從右至左依次為d31,d30,…,d0。信息碼元的輸入端為i。令D=[d0d1…d31]T表示編碼器當前所處的狀態,I=[i63i62…i0]表示第1至第64個時鐘的信息碼元輸入,向量Dˊ=[d0ˊd1ˊ,…d31ˊ] T表示編碼器的下一個狀態,D(64)表示64個時鐘之后CRC編碼器所處的狀態。則設計64位并行CRC邏輯編碼器,就是找出函數關系D(64)=f(D,I)。
do'=d31+i63
d1'=d0+d31+i63
d2'=d1+d31+i63
d3'=d2
…
d31'=d30
寫成行列式,有D'=TD+Si63
其中:

2個時鐘之后編碼器的狀態為:
D''=TD'+Si62=T)TD+Si63)+Si62=T2D+TSi63+Si62
依此類推,有:
D(64)=T64D+T63Si63+T62Si62+…+TSi1+Si0 (2)
這里所有矩陣運算和代數運算中的加號的語義都是模2加法。為了。設計64位并行CRC電路,必須計算(2)式中的大規模矩陣乘法T64、T63S等。
2 代入法
矩陣法的優點在于其直觀性。但是需要做大規模乘法運算。下面討論的代入法能夠得到與矩陣法相同的結果。同時可以避免大規模矩陣乘法運算。設8比特并行CRC-32電路的初始狀態是d31,d30,…,d0,輸入是i7,i6,…,j0,輸出是z31,Z30,…,z0。利用前面所述的矩陣法,可以得出8比特并行CRC-32編碼器的組合邏輯表達式。如表1所示。
即:
z31=d23+d29+i5;
z30=d22+d31+i7+d28+i4
…
z0=d24+d30+i6+i0
表1 8位行CRC邏輯表
| z0 | d24,d30,i6,i0 |
| z1 | d25,d31,i7,i1,d24,d30,i6,i0 |
| z2 | d26,i2,d25,d31,i7,i1,d24,d30,i6,i0 |
| z3 | d27,i3,d26,i2,d25,d31,i7,i1 |
| z4 | d28,i4,d27,i3,d26,i2,d24,d30,i6,i0 |
| z5 | d29,i5,d28,i4,d27,i3,d25,d31,i7,i1,d24,d30,i6,i0 |
| z6 | d30,i6,d29,i5,d28,i4,d26,i2,d25,d31,i7,i1 |
| z7 | d31,i7,d29,i5,d27,i3,d26,i2,d24,i0 |
| z8 | d0,d28,i4,d27,i3,d25,i1,d24,i0 |
| z9 | d1,d29,i5,d28,i4,d26,i2,d25,i1 |
| z10 | d2,d29,i5,d27,i3,d26,i2,d24,i0 |
| z11 | d3,d28,i4,d27,i3,d25,i1,d24,i0 |
| z12 | d4,d29,i5,d28,i4,d26,i2,d25,i1,d24,d30,i6,i0 |
| z13 | d5,d30,i6,d29,i5,d27,i3,d26,i2,d25,d31,i7,i1 |
| z14 | d6,d31,i7,d30,i6,d28,i4,d27,i3,d26,i2 |
| z15 | d7,d31,i7,d29,i5,d28,i4,d27,i3 |
| z16 | d8,d29,i5,d28,i4,d24,i0 |
| z17 | d9,d30,i6,d29,i5,d25,i1 |
| z18 | d10,d31,i7,d30,i6,d26,i2 |
| z19 | d11,d31,i7,d27,i3 |
| z20 | d12,d28,i4 |
| z21 | d13,d29,i5 |
| z22 | d14,d24,i0 |
| z23 | d15,d25,i1,d24,d30,i6,i0 |
| z24 | d16,d26,i2,d25,d31,i7,i1 |
| z25 | d17,d27,i3,d26,i2 |
| z26 | d18,d28,i4,d27,i3,d24,d30,i6,i0 |
| z27 | d19,d27,i5,d28,i4,d25,d31,i7,i1 |
| z28 | d20,d30,i6,d29,i5,d26,i2 |
| z29 | d21,d31,i7,d30,i6,d27,i3 |
| z30 | d22,d31,i7,d28,i4 |
| z31 | d23,d29,i5 |
下文用"+"表示按位模2和運算,"{,}"表示鏈接運算。從CRC的(1)式很容易得出以下算法:
算法1:已知序列N的CRC-32為A[31:0],序列B(=[b7,b6,…,b0])的CRC-32碼為Y[31:0]。序列A[31:24]的CRC-32為X[31:0],則延拓序列{N,B}的CRC-32碼為{Y[31:24]+X[31:24]+A[23:16],Y[23:16]+X[23:16]+A[15:8]+A[7:0],Y[7:0]+X[7:0]}。
推論:已知序列N的CRC-32為A[31:0],序列A[31:24]的CRC-32為X[31:0],則補0延拓序列{N,O}的CRC-32碼為{X[31:24]+A[23:16]+A[15:8],X[15:8]+A[7:0],X[7:0]}。
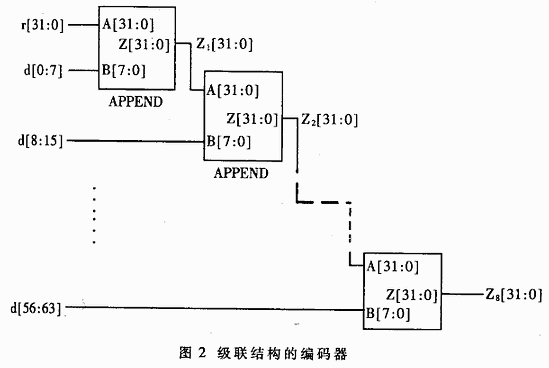
利用上述算法構造APPEND模塊,其端口A和B分別表示前導序列的CRC和延拓的8比特序列,則其輸出端口Z為拓展之后序列的CRC。圖2利用APPEND模塊構造了級聯結構的64比特并行CRC編碼器。這種級聯構造的編碼器設計比較簡單。其中間節點:
Z1(n)=f(r,d[0:7] n[31,0]
Z2(n)=f(Z1,d[8:15])=f(f(r,d[0:7]),d{8:15])
… (3)
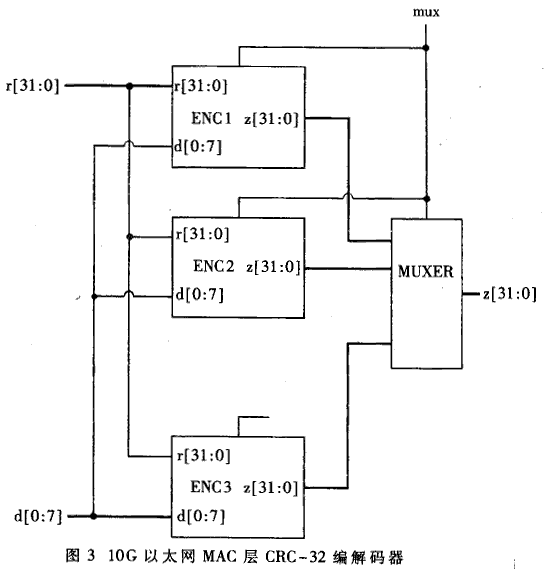
顯然(3)還可以進一步化簡。冗余的邏輯使得這種級聯結構占用芯片面積大,且只能用于低速場合。對(3)進一步化簡,可以得到Z2的最簡異或表達式。同理可以得到Z3…Z8的表達式。Zl,Z2,…,Z8分別對應8比特、16比特、……、64比特的并行CRC運算表達式。具體表達式限于篇幅不在這里給出。Z8中最長的異或運算表達式有52項參加運算,如果使用4-異或門則只需要用三級,即能在一般CMOS工藝的一級傳輸延遲時間之內完成。當用于以太網接入系統時,因為以太網幀不一定結束在64比特邊界,因此編碼器應該有同時計算8、16、24、……、64比特并行編碼的能力。具體電路如圖3。因為一般情況下大量用到64比特并行編碼,因此平時使能信號mux使其他7個編碼模塊不工作以降低功耗。在幀尾部根據具體情況使用這7個模塊進行剩余字節的編碼。
3 流水線法
矩陣法和代入法本質上都是設計直接并行編碼電路的方法,二者的最終效果是一樣的。直接并行實現的CRC編碼電路控制邏輯比較簡單,但是需要進行復雜的組合邏輯運算。為了在更高頻率下進行并行CRC編碼,可以進一步用流水線的方法簡化編碼邏輯,所付出的代價是整個幀的處理延遲了8個時鐘周期。圖4給出了CRC編碼的流水線實現。將并行輸入的64比特分成7個字節,分別用D0、D1、……、D7表示。P模塊(P0~P7)計算形如"Di,O,O,O,O,O,O,O,Di"的序列的CRC,其中Diˊ,是Di位置上的上一次輸入。Diˊ的CRC碼由端口R[31:0]輸入,Di由端口D[7:0]輸入,結果由Z[31:0]端口輸出。
C模塊(C1~C7)的輸入是"D0,O,O,O,O,O,O,O,D0'和"D1ˊ,O,O,O,O,O,O,O,D1"的CRC(分別由端口R1和R2輸入),輸出是"D0ˊ,D1ˊ,O,O,O,O,O,O,D0,D1" CRC。求P的邏輯表達式時,重復應用算法1的推論,可以求出"Diˊ,O,O,O,O,O,O,Di"的CRC碼,再應用算法1,就可以求出"Diˊ,O,O,O,O,O,O,O,Di"的CRC碼。直接應用算法1可以求出C模塊的邏輯表達式。P模塊和C模塊進行異或運算的長度遠小于直接并行CRC電路中的ENC8模塊,因此更有利于在高速電路中應用。

4 10G以太網接入系統中的CRC編解碼器設計
10G以太網接人系統所需接口速率高達10Gbps以上。從降低系統功耗和芯片制造成本的角度考慮希望接口能工作在200MHz以下。采用并行化設計雖然可以降低系統時鐘頻率,但也從以下兩方面增加了設計難度。首先,數據通路的并行程度越高,對它的控制就越復雜。系統采用8字節并行數據通路,則發送的以太網幀可能在8個并行字節中的任意一個位置上結束,控制邏輯的設計就必須考慮所有這些可能性并逐一做出相應的處理。其次,系統中的CRC編碼器、擾碼器等的設計須采用并行算法。為了滿足IEEE802.3協議對以太網幀CRC編碼的要求,實際的編解碼器模塊還需要能對輸入輸出信號進行任意字節數的求反運算。考慮到10G接入系統的復雜性,該模塊功能應該高度集成化,以便用宏信號端口對其進行操作。在對收到的以太網幀進行校驗時,沒必要先計算不包括FCS域的序列的CRC編碼(結果取反)再與FCS域做對比。在編碼正確且沒有誤碼的情況下,對整個以太網幀(包括FCS域)進行結果不取反的CRC編碼的結果應該為序列0xC704DD7BH。采用這種判別方法,無需在幀的結束前停止計算CRC編碼,因而可以大大簡化電路設計。
5 CRC編碼器的實現
本文提出的各種算法的硬件實現已經通過了FPGA驗證,并被應用到具體芯片。使用Xilinx公司的Virtex2系列FPGA中的XC2V1000分別仿真了采用上述代入法和流水線法設計的CRC編碼器和解碼器,驗證了設計方法的正確性。在綜合考慮邏輯復雜度、所占用的芯片面積和工藝要求后,最終在所設計的10G以太網接入芯片中,采用了代入法設計的CRC編碼器和解碼器。
10G以太網接入系統中需要采用并行CRC編碼器。本文提出了基于組合邏輯的直接實現和基于流水線的實現方法。其中直接實現的方法又分為矩陣法和代入法兩種。經過具體推導發現直接實現的編碼器可以滿足延時要求,因而被本系統所采用。而基于流水線的設計因為其延時較小,可以用于更高速的場合。本文提出的三種并行化設計方法已經通過了硬件驗證。這些設計思想同樣適用于其他線性移位寄存器,如擾碼器的設計。
 電子發燒友App
電子發燒友App




















評論