|作者：李穎1?孫昌璞1，2

(1?中國工程物理研究院研究生院) (2 北京計算科學研究中心)

■推薦理由

量子計算是具有巨大潛在價值和顛覆性的科技發展方向，其原理、算法和實現方案并不為大眾所熟悉。本文介紹了量子計算的基本概念、與經典計算的差異、發展現狀以及未來發展的瓶頸，使讀者可以系統、準確并客觀地理解和看待不斷涌現的新發展。

摘 要??量子計算技術近年來快速發展并受到廣泛關注。文章將介紹一些量子計算的基本概念、現狀以及遠期和近期的主要挑戰，使讀者可以更準確地理解一些新近的進展，避免誤解。通用量子計算機的主要應用之一是破解RSA密碼。沒有量子糾錯，我們很難實現密碼破解規模的量子計算。因此，量子計算技術的一大挑戰是如何實現有量子糾錯保護的量子計算，也就是容錯量子計算。通過介紹現有的實驗技術，將發現目前已經可以在實驗中實現錯誤率低于容錯閾值的量子門，但容錯量子計算離實際應用還有距離。主要的困難在于，量子容錯需要數量巨大的低錯誤率的量子比特，超出了現有技術能達到的水平，需要進一步的發展。有噪聲中等規模量子計算有可能在近期內成為現實，目前仍有一些理論和技術方面的瓶頸問題需要深入研究。在看到量子計算技術巨大潛在價值和長足進步的同時，有必要了解有哪些亟需解決的問題，直面關鍵、攻堅克難。

01? 引言

計算機技術已經引起了經濟和社會的巨大改變，其發展得益于傳統量子物理的研究。晶體管是計算機的主要元件，有了量子力學理論我們才能夠理解這種半導體器件的基本原理。在過去的四五十年當中，集成電路中的晶體管數量大概每一年半增長一倍，被稱為摩爾(Moore)定律。然而，目前這個趨勢正在放緩。在這個時候，量子物理研究有可能再一次從根本上突破瓶頸并促進計算機技術的大規模發展。 ? 與今天廣為使用的計算機(我們稱之為經典計算機)相比，量子計算機通過一種完全不同的方式進行計算，因此給計算技術帶來了全新的可能性。量子力學理論創立于20 世紀初，經由大量的物理實驗驗證，業已成為半導體和現代化學的理論基礎。在量子力學中，物理系統的狀態需要用波函數來描述，存在不是非黑即白的狀態，被稱為量子疊加態。同時，量子力學預言了波函數的相干、糾纏等經典物理理論中沒有的現象。雖然我們很難在日常生活中直接看到這些現象，但它們都能在實驗室中被觀測到。量子計算機的“量子”指的就是在計算中利用量子相干、糾纏等效應，進而能夠用比經典計算機更短的時間完成某些特殊計算。這正是我們研發量子計算機的最主要原因。除此以外，量子計算技術還促進了基礎研究和其他量子技術，例如量子通訊和量子傳感等。 ? 雖然經歷了近年來的快速發展，與成熟的經典計算機技術相比，量子計算機技術仍處于初級階段。量子計算機的概念在20 世紀80 年代被提出[1，2]，此后在很長的時期內屬于基礎研究的范疇。目前，量子計算剛剛由基礎研究轉向工程實現和應用研究。我們還沒有發現任何基本問題可能導致最終無法實現有應用價值的量子計算機；與此同時，也很難預測這一轉變的最終完成需要多長時間[3]。 ? 下面，我們將具體介紹量子計算機的概念、優勢以及實現方法。除此以外，還會介紹一些典型的量子計算物理系統，以及探討在近期內實現量子計算技術實際應用的可能性。希望通過這些介紹，使專家和領域外的人士對量子計算的概念和發展態勢有一個科學的理解。

02? 通用量子計算機

從算法的角度來說，量子計算機具有比經典計算機更強大的計算能力。這個想法最初是由費曼(R. Feynman)和馬寧(Y. Manin)在20 世紀80 年代初提出[1， 2]。自20 世紀40 年代美國核武器研究起，數值計算被廣泛應用于物理學以及其他學科的研究中。其中重要的一項應用是對物理系統的數值模擬。自然界的物理系統均為量子系統。然而，由于記錄和處理量子態需要很大的信息存儲空間，利用經典計算機對量子多體系統進行模擬是非常困難的。但是，量子計算機沒有這個問題。如果經典計算機無法精確模擬量子多體系統而量子計算機可以，那么不言而喻，量子計算機優于經典計算機。 ? 1985 年，多伊奇(D. Deutsch)提出了量子計算機的模型——通用量子計算機(或量子圖靈機)[4]。任意一種量子算法均可以利用通用量子計算機實現。量子計算機是由許多量子比特(二態量子系統)組成的物理系統。對每個量子比特， |0> 和|1>是兩個完全可區分的量子態，它們分別對應二進制數中的0 和1。量子比特和經典比特的差別在于，量子比特可以處于0 和1 的量子疊加態，用a|0> +b |1> 表示，這里系數a 和b 刻畫了量子比特的具體狀態。量子計算有很多方式，其中廣泛使用的模型是量子線路，也就是通過在量子比特上執行一系列的邏輯操作來實現量子計算，如圖1所示。這些邏輯操作包括：量子比特的初始化、量子態的幺正變換以及對量子比特信息的讀取。

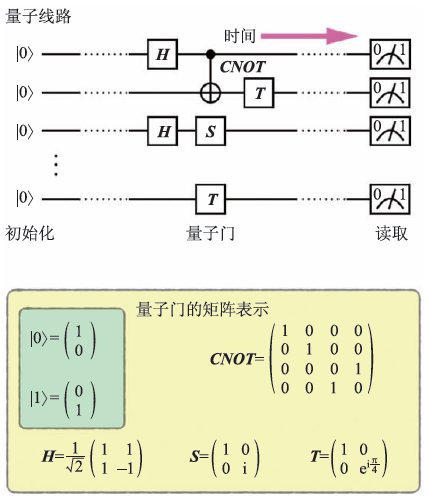
圖1 量子線路和量子門。量子線路由量子比特的初始化、一組量子門以及最終的信息讀取組成。其中的量子門可以由矩陣表示

與經典計算機中的通用邏輯門類似，在量子計算機中任意的幺正變換均可以通過一組有限的幺正變換(量子門)的組合以任意的精確度近似。這樣一組量子門被稱為通用量子門。例如，Hadamard門(H)、π/4 相位門(S)、π/8 相位門(T)以及受控非門(CNOT)構成一組通用量子門[5]。這里面H、S 和T為單量子比特門，CNOT為兩量子比特門(圖1)。利用這些量子門，不僅可以實現任意的量子算法，還可以實現任意的經典算法。從這個意義上說，顯然量子計算機的計算能力是大于等于經典計算機的。 ? 1986 年，多伊奇和喬沙(R. Jozsa)提出了一個計算問題來表明量子計算機的確在解決某些問題上具有優勢[6]。他們提出的問題是判斷一個函數f :{x}→{0，1}對于不同的輸入x 是否給出相同的輸出0 或1。函數f 需要滿足一定的條件，這里不再贅述。對于輸入為一個比特的情況，也就是x有兩個取值0 和1，用經典計算機解決這個問題需要計算f 至少兩次。而用量子計算機只需要計算f?一次， 這個量子算法被稱為多伊奇— 喬沙(Deutsch—Jozsa)算法。當輸入比特增多的時候，確定性經典算法需要計算f 的次數隨著比特數量指數增長，而量子算法仍然只需要計算f 一次。 多伊奇—喬沙問題 ? ? 在多伊奇—喬沙問題中，函數f 需要滿足如下條件：要么所有的輸出均相同；要么在所有的輸入x中，一半的輸出為0，一半的輸出為1。對于n 個輸入比特的情況，總共有2n種可能的輸入x，有可能在查看2n/2+1 種輸入以后才發現有不同的輸出。因此，在經典計算中確定性的解決多伊奇—喬沙問題需要進行2n/2+1 次計算。

1994 年，肖爾(P. Shor)提出了能夠解決因數分解問題的量子算法，被稱為肖爾(Shor)算法[7]。利用已知最好的經典算法，因數分解所需的時間隨著整數長度次指數增長。由于指數函數增長非常快，當整數達到一定長度時，經典計算機無法有效地進行因數分解。廣為使用的RSA密碼系統正是基于這一點。然而，量子算法所需的時間隨著整數長度代數增長，要遠遠慢于指數函數。因此，量子計算機可以更快地對大整數進行因數分解。利用量子計算機，我們可以破解經典計算機無法破解的密碼，給密碼系統的安全性帶來了挑戰。當然，對于有些密碼算法，還沒有發現像肖爾算法這樣可以進行破解的量子算法。因此，抵御量子計算對密碼安全的威脅有兩種方式，一種是基于量子物理的量子密鑰分發，另一種是后量子密碼，也就是量子計算還無法破解的經典密碼算法[8]。 ? 1996 年，勞埃德(S. Lloyd)提出了可以模擬局域相互作用量子系統演化的通用量子計算機算法[9]。根據這個算法，模擬量子系統演化的誤差可以趨近于零，而算法所需的資源隨著子系統個數、誤差等參數的變化是一個代數函數。因此，通用量子計算機可以有效模擬量子系統演化。基于對演化的模擬，量子計算機還可以用來求解某些量子系統的基態能量等問題。量子系統的演化和基態能量是兩個非常重要的計算問題，在物理、化學和材料等學科的研究中均有應用。

目前計算機已經廣泛應用于日常生活的方方面面。但在計算機技術普及以前，它的兩個主要應用是密碼破譯以及科學計算和模擬。非常巧合的，量子計算機兩個重要的算法——肖爾算法和量子模擬算法分別對應了這兩種應用。這兩個算法有清晰的應用背景以及對經典算法的優勢，因此極具代表性。如果能夠在量子計算機上演示這兩個算法，并且用來解決經典計算機無法解決的實例，或許可以認為最終實現了通用量子計算機。 ? 除了本文介紹的，目前還有很多其他的量子算法[10]。應該注意到，不是對于所有的計算問題量子算法都有指數加速。在算法方面量子計算機和經典計算機的對比有大量計算復雜性理論的研究[5]。 ? 到目前為止，所有的結論都是基于擁有通用量子計算機這一假設。那么，我們有可能制造一臺通用量子計算機嗎？事實上，由于普遍存在的退相干現象，嚴格的幺正變換量子門是不可能百分百實現的。關鍵是這種退相干對計算結果有多大影響，是否在許可誤差范圍內。

03? 退相干 量子計算所需的量子門是幺正變換。在量子力學理論中，幺正變換描述了一個封閉系統的演化。然而，在自然界中我們還沒有發現真正的封閉系統：一個物理系統總是或多或少地與外界環境存在相互作用。由于相互作用的影響，系統演化不僅由系統本身決定還取決于環境的狀態。其結果是系統演化一般不再是幺正變換。我們用完全正定映射來描述量子系統最一般性的演化。有些非幺正演化會使量子系統逐漸失去相干性，也就是量子疊加態無法持續，這個過程被稱為退相干。 ? 退相干會導致量子算法失去優勢。1998 年，本文作者之一及其合作者討論了退相干對肖爾算法的影響，發現退相干會降低成功求解因數的概率[11]。當概率過低時，量子算法的效率不再高于經典算法。事實上，在物理系統中執行的量子門相對理想量子門的任何偏離都有可能導致量子計算的結果錯誤，進而量子算法失效。

退相干在自然界中是廣泛存在的。與此同時，有一些物理機制可以用來抑制退相干。當環境對系統的影響具有某些對稱性的時候，可能存在一個不發生退相干的量子態子空間，因此存儲在子空間內的量子信息可以不受退相干的影響[11-13]。如果環境引起的噪聲在時間上有關聯，動態解耦等方法可以用來抑制退相干的發生[14，15]。這些方法可以在很大程度上改進物理系統在量子計算中的性能，但計算錯誤的發生仍然是無法避免的。因此，需要在算法的層面對計算錯誤進行處理：雖然在計算過程中還是會發生錯誤，但可以避免錯誤對最終計算結果的影響。 退相干導致的兩種計算錯誤 ? ? 我們可以將量子計算機中的錯誤分為兩種：比特錯誤和相位錯誤。比特錯誤導致量子比特0 和1 的取值發生改變，相位錯誤導致疊加態的相位發生變化。對于一個處于疊加態a |0> + b|1> 的量子比特，比特錯誤導致狀態改變為a |1> + b|0> ，相位錯誤導致狀態改變為a |0> - b|1> 。在經典計算機中也存在比特錯誤，但相位錯誤是量子計算機獨有的。量子計算機中任何的錯誤都可以分解為兩種錯誤的組合。 ? ? 04? 量子糾錯碼和容錯量子計算

量子糾錯碼可以用來解決退相干等硬件的不完美導致的計算錯誤問題。在錯誤的分布滿足某些條件的情況下，我們可以把最終計算結果出錯的概率降得任意低，這被稱作容錯量子計算。當然，量子糾錯是有代價的。為了降低最終出錯率，需要使用很多的量子比特來進行編碼。進行容錯量子計算的首要條件，也就是錯誤率低于容錯閾值(亞閾值)的初始化、量子門以及讀取等操作已經能夠在實驗中被演示。目前看來，在錯誤率低于閾值的條件下，巨大的量子比特數量是最終實現容錯量子計算的主要障礙。

4.1?量子糾錯碼

量子糾錯碼是經典糾錯碼在量子信息的推廣。首先來了解什么是經典糾錯碼。最簡單的糾錯碼是重復碼(repetition code)，也就是將要保護的信息重復存儲(圖2)。在日常生活中，我們會經常使用這種保護信息的方式，例如將重要的文件復制一份。事實上，這同樣也是經典信息比量子信息更穩定的原因之一。在機械硬盤上，我們通過控制鐵磁材料的極化方向來存儲信息。其中少數粒子極化方向的錯誤不會影響對整體信息的讀取。糾錯碼也是類似的。如果只有少數比特的信息發生了錯誤，我們可以將出錯的比特找出來，進而實現對信息的保護。找出錯誤的方式有兩種：一種是多數決定法，也就是數一數哪一種比特(0 或1)比較多，多的那一種應該代表了正確的信息；另一種是宇稱查驗，也就是查驗相鄰比特的取值是否相同，不同則意味著其中一個出錯了。對于經典糾錯來說，兩種糾錯方式都有效。

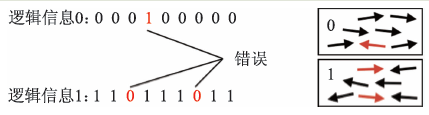
圖2 經典糾錯碼和經典信息存儲

和經典糾錯相比，量子糾錯不僅需要處理比特錯誤，還需要處理相位錯誤。1995 年，肖爾提出了第一個量子糾錯碼——肖爾(9 量子比特)碼，通過兩次利用重復碼來處理兩種錯誤[16]。基于相同的思想，通過結合兩個經典糾錯碼分別用來處理比特錯誤和相位錯誤，考得本克(R. Calderbank)、肖爾和斯特恩(A. Steane)提出了一系列的量子糾錯碼，并以他們三個人的名字命名為CSS碼[17，18]。當然，有的量子糾錯碼是以其他方式構造的。 ? 由于對量子比特的讀取會破壞量子疊加態，量子信息不能以讀取信息再按照多數決定的方式糾錯。在量子糾錯中，糾錯的方式是宇稱查驗，也就是通過查驗量子比特之間的關系查找錯誤。量子糾錯中的宇稱查驗是對一組物理可觀測量(厄米算符)的測量，一般來說是一組相互對易的泡利算符。不同的量子糾錯碼對應了不同的一組算符。任何一個量子比特上的錯誤都會反映為算符測量結果的改變，也就是說能夠在測量中被觀測到。

宇稱查驗會犧牲一些量子比特的自由度。對于n 個量子比特的糾錯碼，如果宇稱查驗涉及s 個獨立的泡利算符，那么我們可以存儲k ≤ n - s 個被保護的量子比特信息。這是由于這些泡利算符正確值對應的量子態空間的維度是2n－s，因此在這個子空間內可以存儲最多n－s 個量子比特信息。編碼用到的n 個量子比特被稱為物理量子比特，被保護的k 個量子比特被稱為邏輯量子比特。在量子糾錯中，每一個物理量子比特都對應了一個具體的兩量子態物理系統，而一個邏輯量子比特則涉及到多個甚至所有物理量子比特，是最終用來存儲信息和計算的量子比特。 宇稱查驗和斯特恩7量子比特碼 ? ? 我們用X和Z表示兩個泡利算符，每個泡利算符有＋1 和－1 兩個本征值。比特錯誤會改變Z的值，相位錯誤會改變X的值。圖中每一個圓對應了一個量子比特。對于斯特恩碼，需要進行6 種宇稱查驗，分別是每一個四邊形上4 個量子比特泡利算符的乘積，ZZZZ和XXXX。經過觀察可以發現，任何一個比特錯誤或相位錯誤都會導致特定一組宇稱查驗結果（即XXXX和ZZZZ的取值） 的改變。因此，這些錯誤可以被發現并且糾正。

有沒有一種量子糾錯碼，它的宇稱查驗和重復碼類似，只是對近鄰量子比特的測量？由于在物理系統中量子比特之間往往是近鄰相互作用，這樣的糾錯碼更容易實現。1997 年，凱達耶夫(A. Kitaev)提出了拓撲碼[19]，根據邊界條件的不同，也被稱為環面碼或表面碼(圖3)。此后又發現了其他具有類似性質的量子糾錯碼。對于量子計算來說，目前綜合看來表面碼可能是糾錯碼最好的選擇。

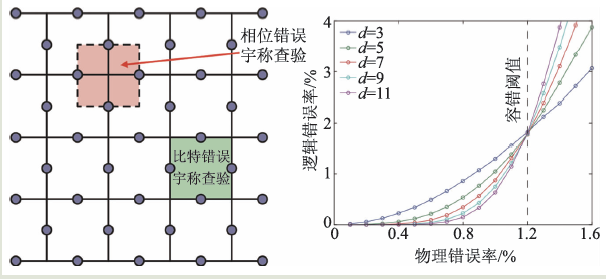
圖3 表面碼和容錯閾值

4.2 容錯閾值

在量子計算中，需要通過對物理量子比特的操作來實現量子糾錯所需要的宇稱查驗。而每一次操作都有一定概率引入錯誤，有可能導致糾錯本身起到負面作用。因此，如果量子糾錯能夠起到預期效果，其前提條件是宇稱查驗過程中產生的錯誤不會使得錯誤沒有減少反而增加了。這個條件被量化為容錯閾值：當單次操作的錯誤率小于閾值的時候，量子糾錯才能起到應有的作用。 ? 對于表面碼來說，當物理量子比特單次操作的錯誤率低于閾值的時候，糾錯后邏輯量子比特的錯誤率隨著表面碼尺寸(碼距)的增加而降低，如圖3 所示。事實上，這種情況下邏輯錯誤率隨著碼距指數衰減。因此，我們可以通過增加碼距，也就是使用更多的物理量子比特，來降低邏輯錯誤率。只要物理量子比特足夠多，邏輯錯誤率就會足夠低。數值模擬表明表面碼的錯誤率閾值大約是1%[20]。 關于容錯閾值的兩點說明 ? ?

(1)閾值一般是在對錯誤分布的合理假設下得到的，假設與真實的物理系統之間還存在著差異。一般來說，假設包括每次操作的錯誤是獨立分布的。常用的模型是去極化模型，即當錯誤發生的時候，相應物理量子比特的量子態完全被破壞。

(2)閾值是對單次操作的錯誤率來說的。例如整個計算包括N次操作，每次操作的錯誤率為p，那么在物理量子比特上發生錯誤的個數大概是Np。即使在Np>>1 的情況下，只要p 小于閾值并且量子糾錯碼足夠大，邏輯量子比特出錯的概率還是可以足夠低。

4.3?容錯量子計算

通過查驗物理量子比特之間的關系，邏輯量子比特被保護起來了。除此以外，我們還需要對邏輯量子比特進行操作來實現通用量子計算。并且這些操作不應該破壞對邏輯量子比特的保護。在這方面已經有大量的研究。為了能夠進行通用量子計算，需要一組邏輯量子比特操作，包括初始化、通用量子門以及讀取。其中某些操作可以直接進行而不明顯增加邏輯錯誤率，另外一些操作需要通過引入魔術態[21]等處理方法來進行。容錯量子計算的過程如圖4 所示，這里不再贅述。總的來說，理論上基于邏輯量子比特的通用量子計算是可行的。

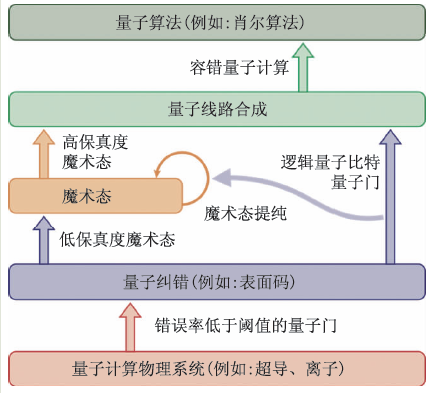
圖4 容錯量子計算

目前看來，表面碼可能是實現容錯量子計算最好的選擇。首先，表面碼具有較高的容錯閾值(～1%)。其次，表面碼僅需要在近鄰量子比特之間進行宇稱查驗，容易在物理系統中實現。雖然通過CSS碼的級聯可以得到更高的閾值(～3%)[22]，但需要在遠距離量子比特之間進行宇稱查驗，也就是需要量子計算機內部的高保真度量子態傳輸，因此在物理系統中實現的難度更高。 ? 實現容錯量子計算需要一臺擁有大量低錯誤率量子比特的量子計算機。在亞閾值的條件下，只要物理量子比特數量足夠多，碼距足夠大，我們就能夠運行任意復雜的量子算法。需要的量子比特數量由錯誤率以及算法決定。對于表面碼，操作邏輯量子比特的錯誤率可以用P～d(100p)(d+1)/2來粗略估計，其中p 是物理錯誤率，d 是碼距[23]。一個邏輯量子比特需要的物理量子比特數量大約為(2d－1)2。如果我們考慮利用肖爾算法分解RSA系統中1000 位的二進制整數，邏輯操作的數量大約在1011的數量級，因此邏輯錯誤率P 需要達到10-12的水平。我們還假設需要1000 個邏輯量子比特用于存儲整數，并需要大約10 倍的量子比特用于輔助，包括魔術態制備等。這樣就能估計所需要物理量子比特的總數。這里僅做最簡單粗略的估計，結果如圖5所示。

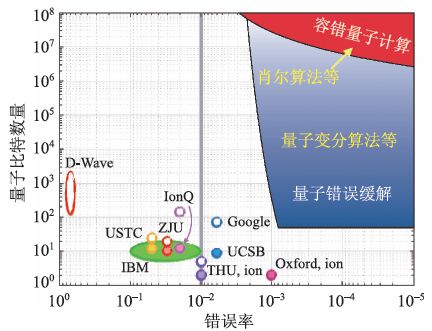
圖5 量子計算系統參數。灰線對應錯誤率p=1%，為表面碼的閾值。D-Wave 系統為模擬量子計算機，沒有兩量子比特門錯誤率。空心代表沒有找到報道兩量子比特門錯誤率測量實驗結果的文獻。作者注意到關于USTC量子門錯誤率的文獻中提到，利用隨機校準測量的其系統中單個兩量子比特門的錯誤率一般低于1%[30]

我們可以發現，實現容錯量子計算需要錯誤率明顯低于閾值(到0.1%附近及以下)以及百萬以上的物理量子比特。這對于目前的技術來說還是無法實現的。 ? 容錯量子計算需要經典計算機的參與。特別是表面碼的解碼過程(也就是根據宇稱查驗的測量結果查找錯誤的過程)，需要消耗一定的經典計算資源。而且碼距越大，所需的計算資源越多。因此，量子計算機不會簡單取代經典計算機，除非量子計算機在速度、成本特別是精確度等方面達到了經典計算機的水平。

05? 量子計算的物理系統

我們已經發展出了眾多可以用于量子計算的物理系統，包括超導量子比特、囚禁離子、量子點、中性冷原子、光學量子計算和拓撲量子計算等。目前已經能夠在實驗中演示亞閾值的量子比特操作(包括初始化、量子門以及讀取)。其中代表性的是2014 年在超導量子比特系統中實現了錯誤率大約0.6%的兩量子比特門，同年在囚禁離子系統中演示了錯誤率大約0.1%的兩量子比特門。這些試驗結果表明亞閾值的量子計算系統在技術上是可行的。 ? 我們主要關心的是兩量子比特門。這是由于一般來說相較于其他操作，兩量子比特門的錯誤率更高，并且在宇稱查驗中影響更大。在這些能夠演示亞閾值操作的實驗系統中，量子比特數量都比較少。因此，按照容錯量子計算的方案，量子糾錯可以降低操作邏輯量子比特的錯誤率，但目前還沒有在實驗中被成功演示。在接下來對實驗系統的介紹中，我們提到的量子比特均為物理量子比特，而不是被糾錯碼保護的邏輯量子比特。 ? 超導量子比特系統——作為固態系統具有較好的可擴展性。2011 年D-Wave 發布的其第一臺量子計算系統具有128 個量子比特，至2017 年最新的系統已經具有2000 個量子比特[24]，體現了超導系統良好的可擴展性。但D-Wave 的系統是模擬(analog)量子計算系統，不是本文主要討論的基于量子線路的通用量子計算系統。在通用量子計算方面，加州大學圣巴巴拉分校(UCSB)的超導量子計算實驗室的9 量子比特系統可以實現錯誤率大約0.6%的兩量子比特門[25]。2018 年Google 發布了基于相同設計的72 量子比特系統[26]。自2016 年起，IBM投入大量資源研發并提供開放的量子計算系統，可以通過云訪問。在其數個量子計算系統中，最早的系統有5 個量子比特，目前在線的系統最多有20 個量子比特，兩量子比特門錯誤率由大約1%到10%不等[27]。 ? 浙江大學(ZJU)的超導量子計算實驗室可以在10 量子比特系統中實現錯誤率大約3%的兩量子比特門，并且兩量子比特門可以在任意一對量子比特之間進行，實現了全耦合[28]。基于相似的設計，他們還研發了能夠全耦合的20 量子比特系統[29]。中國科學技術大學(USTC)的超導量子計算實驗室可以在12 量子比特系統中實現錯誤率大約5%的兩量子比特門[30]。其最新的系統具有24 個量子比特[31]。

囚禁離子系統——具有很高的精確度，兩量子比特門的錯誤率可以達到0.1%以下，遠遠低于容錯閾值。牛津大學(Oxford，2014 年)和美國國家標準技術研究所(NIST，2016 年)的囚禁離子實驗室利用不同的離子分別成功演示了錯誤率大約0.1%的兩量子比特門[32，33]。然而，這兩個實驗系統都僅有兩個離子量子比特。2018 年，IonQ 發布了160 個量子比特的系統，其技術可以在13 個量子比特的系統實現錯誤率2%以下的量子門[34]。清華大學(THU)的囚禁離子實驗室目前可以囚禁5個離子量子比特并實現通用量子門，在兩量子比特系統中能夠達到大約1%的兩量子比特門錯誤率[35，36]。一般認為通過增加單個離子阱中的離子個數來增加量子比特數量是不可擴展的。囚禁離子系統可以利用分段離子阱[37]或網絡化的方式進行擴展。 ? 網絡量子計算系統——網絡化是擴展量子計算系統的一個方式[38]。對于囚禁離子系統，可以利用光學系統將眾多離子阱(節點)耦合起來，每個節點僅需有少數幾個離子量子比特(圖6)。通過光子量子比特可以在不同的節點之間實現對離子量子比特的操作，進而整個離子阱網絡可以作為一個可擴展的量子計算系統使用。一般來說節點間操作錯誤率較高。理論研究表明，只要節點內操作錯誤率顯著低于1%，即使節點間操作錯誤率遠遠高于1%，仍然可以進行容錯量子計算[39-41]。牛津大學網絡量子信息技術中心以此為方案在發展離子阱網絡量子計算機[42]。

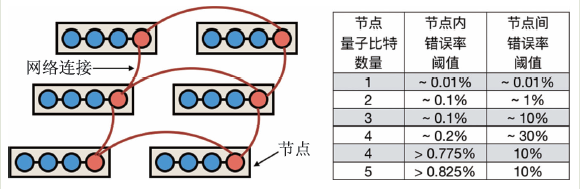
圖6 網絡架構量子計算

網絡化架構對于超導量子比特以及分段離子阱等系統同樣具有意義。對于表面碼量子計算，理想的狀況是制備一個足夠大的二維量子比特陣列，其中所有的近鄰量子比特之間可以進行同樣好的低錯誤率操作。但這樣一個系統需要對量子比特的品質有很好的控制，并且能夠同時優化這個多體系統中的所有操作。而在網絡化架構中，通過犧牲一些操作的精確度以及部分量子糾錯能力，可以顯著降低擴展系統的技術難度。 ? 光學量子計算系統——在超導量子比特或囚禁離子等系統中，制備數百萬的量子比特來實現容錯量子計算是困難的，在近期內難以實現。有一種量子比特相對來說容易制備，也就是光量子比特。利用單光子源、線性光學器件以及單光子探測器可以實現通用量子計算[43]。雖然光量子比特相對容易制備，但實現量子計算需要整合大量的光學器件，不一定比其他系統的難度更低[44]。在光學量子計算和模擬方面，中國科學技術大學的實驗室能夠實現18個光量子比特的量子糾纏態[45]。 ? 拓撲量子計算系統——對量子比特數量的需求是量子糾錯導致的。如果不需要量子糾錯，那么量子比特數量可以大大降低。理論上認為利用拓撲系統中的任意子進行量子計算有可能達到非常高的精確度，因此不需要復雜的量子糾錯[46]。以馬約拉納(Majorana)費米子系統為例，在系統與環境間費米子交換被充分抑制的條件下，雖然還是需要量子糾錯，但用到的量子比特數量會明顯減少[47]。目前還沒有馬約拉納量子比特的實驗演示。有實驗觀測到在半導體—超導雜化系統中發生準粒子污染的時間在微秒量級[48]，與之可比較的是超導量子比特發生退相干的時間同樣在微秒量級。 ? ?

06? 中等規模量子計算和錯誤緩解

容錯量子計算是量子計算技術發展的遠期目標，可能還需要很長一段時間才能實現。但另一方面，一臺僅有幾十個以上量子比特的量子計算機，其行為就很難用經典計算機模擬了。這意味著，在這樣一個中等規模的系統上，就有可能進行有價值的量子計算[49]。近年來提出的量子變分算法[50]就適用于此類系統，可以用來求解量子系統的基態能量或模擬量子系統的演化[51，52]。類似的算法還有量子近似最優化算法等[53]。除此以外，量子模擬器是一個重要的發展方向。 ? 量子計算的指數加速(例如肖爾算法)意味著某些計算問題無法通過發展經典計算技術解決，而這些問題可以用量子計算解決。因此在兩種計算方式的對比中，量子計算比經典計算更具優勢。然而，當比較兩個具體的計算系統的時候，一臺量子計算機和一臺經典計算機，我們應該關心一些更加實際的參數，例如處理器的速度或能耗等。如果以應用為目標，區分兩種計算方式不是最重要的。假如可以在量子計算機上解決某個問題，是量子計算以外其他領域關心的，并在時耗或能耗等方面有一定的優勢，那么應該可以認為量子計算機已經具備應用價值了。 ? 在中等規模量子計算方面，除了要發展相應的量子算法，還需要解決計算錯誤的問題。由于量子比特數量的限制，容錯量子計算方案顯然是不適用的。接下來將介紹中等規模系統中錯誤處理的方式——量子錯誤緩解。 量子模擬器 ? ? 與本文主要討論的基于量子線路的通用量子計算系統不同，一般來說量子模擬器(simulator)是模擬(analog)量子計算系統。量子模擬器是利用一種可控的量子系統(例如超導量子比特系統、囚禁離子系統或冷原子系統等)模擬另一種量子系統，進而研究被模擬系統的性質。雖然同樣用于量子模擬(simulation)，一般來說模擬(analog)量子計算通過系統連續演化完成，而勞埃德提出的通用量子計算算法可以利用量子門實現。

對于有一些計算問題來說，計算結果正確與否很容易查驗。例如因數分解問題，我們很容易用經典計算機查驗一個整數是否是另一個整數的因數。類似的問題包括NP(nondeterministic polynomial time)問題等。如果發生了計算錯誤而得到錯誤的結果，那么最簡單的處理方法就是將計算再重復一次。只要重復的次數夠多，總能得到正確的結果。假設一次計算需要的操作次數是N，單次操作的錯誤率是p，那么整個計算不出錯的概率是(1－p)N。這個概率越低，平均來說我們需要重復的計算次數越多。因此，這個方法在Np不大時是有效的。 ? 對于另外一些計算問題來說，計算結果很難被查驗。例如在量子模擬問題中，計算基態能量或者關聯函數等。對于這類問題，在Np不大的條件下，本文作者之一及其合作者以及IBM量子計算團隊分別提出和發展了兩種處理計算錯誤的方法，它們是錯誤外推[51，54]和隨機錯誤消除[54，55]。 ? 錯誤外推——由于計算錯誤的原因，計算結果可能會偏離正確值，如圖7 所示。如果我們知道錯誤率并且能夠增加錯誤率，那么就可以利用不同錯誤率的計算結果，通過擬合外推的方法，估計在錯誤率等于0 的情況下的正確值。2018 年IBM超導量子計算實驗室演示了錯誤外推法[56]。

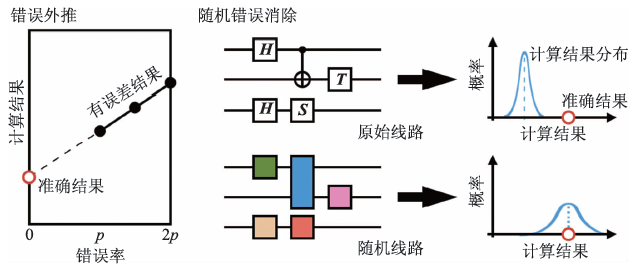
圖7 量子錯誤緩解

隨機錯誤消除——通過在計算中按照錯誤的統計分布隨機地改變原本的量子線路，如圖7 所示，可以使得錯誤對計算結果正負兩方面的影響相互抵消，進而得到正確的結果。2018 年，浙江大學超導量子計算實驗室在10 量子比特系統上進行了演示[57]。2019 年，清華大學離子阱實驗室在實驗中利用隨機錯誤消除將量子門的等效錯誤率降低了一個數量級[36]。

除了錯誤外推和隨機錯誤消除，還有其他一些在中等規模量子計算機上緩解計算錯誤的方法。有些量子算法本身帶有對稱性。例如在分子系統的量子模擬計算中，電子個數往往是一個守恒量。通過查驗類似的守恒量，可以判斷是否發生了錯誤，進而抑制錯誤對最終結果的影響[58，59]。

利用量子錯誤緩解，我們可以擴展能夠進行高精確度量子計算的參數空間。以隨機錯誤消除為例，由于引入的隨機性，計算平均值所需的取樣次數(也就是耗時)將隨之增加，增加的倍數可以用～e4Np來估計[55]。當Np～2 的時候，這個倍數大約是3000，大概還是可以接受的。取樣計算可以并行處理，因此可用的量子比特越多，耗時越短。考慮涉及50 個量子比特以及具有一定線路深度的量子算法，也就是N～502，我們可以粗略估計在中等規模系統上有效進行隨機錯誤消除的參數范圍，結果如圖5 所示。相較于容錯量子計算，這個范圍更加接近今天的實驗技術水平。

07? 結論 量子計算基于自20 世紀初起經由大量實驗驗證的量子力學理論。它的計算方式不同于傳統計算機。在量子計算中信息以量子疊加態的形式存儲，并通過量子態的演化進行計算。量子計算機可以運行以肖爾算法為代表的量子算法，并且在解決某些計算問題方面，量子計算機可以遠遠快于經典計算機。 ? 在量子計算機的物理實現方面，通過量子糾錯可以解決退相干等因素導致的計算錯誤問題。使用量子糾錯的首要條件是亞閾值操作，近年來的實驗進展直接顯示了這個條件是可以達到的。然而，進行密碼破解規模的量子計算所需的量子比特數量巨大，成為了利用肖爾算法等量子算法的主要障礙。目前看來，超導量子比特和囚禁離子系統相較于其他系統具有一定優勢。但鑒于到容錯量子計算還有幾個數量級的差距，很難說我們會在哪一種系統中最終實現通用量子計算機。 ? 受限于現有技術所能提供的量子比特數量，中等規模量子計算有可能在近期內實現應用。我們可以利用量子錯誤緩解抑制計算錯誤，但僅能進行不需要大量操作的量子計算。量子變分算法能夠在這些限制條件下運行，因此適用于中等規模量子計算，并且有希望解決某些經典計算機難以解決的量子化學和材料科學等研究中的重要問題。盡管如此，由于量子變分算法涉及到大規模參數優化并依賴于選取的嘗試量子線路，我們還無法像肖爾算法一樣嚴格從理論上證明其對經典算法的優勢。因此，在這方面還需要從理論上進一步研究量子算法，并在量子計算系統上對算法進行測試。

總之，量子計算是具有巨大潛在價值的顛覆性的科技發展方向，并且近年來在各方面都取得了快速發展。無論是遠期的容錯量子計算還是近期的中等規模量子計算，具有實用價值的量子計算機都需要一定數量的低錯誤率量子比特，當前的實驗技術還無法完全滿足條件。未來的發展既需要從理論上研究量子算法和錯誤處理方法，同時也需要實驗技術在量子比特數量和錯誤率兩方面的進步。這些工作需要踏踏實實的努力，并且要有十年磨一劍的信心和定力。

致謝

感謝袁驍和張靜寧兩位博士提供參考文獻和對部分表述的建議。

參考文獻

[1] Richard F. Int. J. Theor. Phys.，1982，21：467

[2] Manin Yu I. Computable and Noncomputable. Sov. Radio，1980.pp. 13-15

[3] National Academies of Sciences，Engineering，and Medicine. Quantum Computing：Progress and Prospects. Washington，DC：The National Academies Press，2019

[4] Deutsch D. Proc. Royal Soc. A，1985，400：97

[5] Nielsen M A，Chuang I L. Quantum Computation and Quantum Information. Cambridge University Press，2010

[6] Deutsch D，Jozsa R. Proc. Royal Soc. Lond. A，1992，439：553

[7] Shor P W. Algorithms for quantum computation：discrete logarithms and factoring. Proceedings 35th Annual Symposium on

Foundations of Computer Science. IEEE Comput. Soc. Press，1994

[8] https://www.ncsc.gov.uk/information/quantum-key-distribution

[9] Lloyd S. Science，1996，273：1073

[10] https://quantumalgorithmzoo.org/

[11] Sun C P，Zhan H，Liu X F. Phys. Rev. A，1998，58：1810

[12] Duan LM，Guo G C. Phys. Rev. Lett.，1997，79：1953

[13] Zanardi P，Rasetti M. Phys. Rev. Lett. 1997，79：3306

[14] Viola L，Lloyd S. Phys. Rev. A，1998，58：2733

[15] Viola L，Knill E，Lloyd S. Phys. Rev. Lett.，1999，82：2417

[16] Shor PW. Phys. Rev. A，1995，52：2493

[17] Andrew S. Proc. Roy. Soc. Lond. A，1996，452：2551

[18] Calderbank A R，Shor PW. Phys. Rev. A，1996，54：1098

[19] Kitaev A Y. In：Proceedings of the Third International Conference on Quantum Communication，Computing and Measurement，edited by Hirota O，Holevo A S，and Caves C M. New York：Plenum Press，1997

[20] Wang D S，Fowler A G，Hollenberg L C L. Phys. Rev. A，2011，83：020302

[21] Bravyi S，Kitaev A. Phys. Rev. A，2005，71：022316

[22] Knill E. Nature，2005，434：39

[23] Fowler A G，Devitt S J，Jones C. Sci. Rep.，2013，3：1939

[24] https://www.dwavesys.com/d-wave-two-system

[25] Barends R et al. Nature，2014，508：500

[26] https://ai.googleblog.com/2018/03/a-preview-of-bristlecone-googles-new.html

[27] https://quantum-computing.ibm.com/

[28] Guo Q et al. Phys. Rev. Lett.，2018，121：130501

[29] Song C et al. arXiv：1905.00320

[30] Gong M et al. Phys. Rev. Lett.，2019，122：110501

[31] Ye Y et al. Phys. Rev. Lett.，2019，123：050502

[32] Ballance C J et al. Phys. Rev. Lett.，2016，117：060504

[33] Gaebler J P et al. Phys. Rev. Lett.，2016，117：060505

[34] https://ionq.co/news/december-11-2018

[35] Lu Y et al. arXiv：1901.03508

[36] Zhang S et al. arXiv：1905.10135

[37] Kielpinski D，Monroe C，Wineland D J. Nature，2002，417：709

[38] DürW，Briegel H J. Phys. Rev. Lett.，2003，90：067901

[39] Li Y，Barrett S D，Stace T M et al. Phys. Rev. Lett.，2010，105：250502

[40] Li Y，Benjamin S C. New J. Phys.，2012，14：093008

[41] Nickerson N H，LiY，Benjamin S C. Nat. Commun.，2013，4：1756

[42] https://nqit.ox.ac.uk/

[43] Knill E，Laflamme R，Milburn G. Nature，2001，409：46

[44] Li Y，Humphreys P C，Mendoza G J et al. Phys. Rev. X，2015，5：041007

[45]Wang X L et al. Phys. Rev. Lett.，2018，120：260502

[46] Nayak C，Simon SH，SternAet al. Rev.Mod. Phys.，2008，80：1083

[47] Li Y. Phys. Rev. Lett.，2016，117：120403

[48] Albrecht S M. Phys. Rev. Lett.，2017，118：137701

[49] Preskill J. Quantum，2018，2：79

[50] Peruzzo A et al. Nat. Commun.，2014，5：4213

[51] Li Y，Benjamin S C. Phys. Rev. X，2017，7：021050

[52] McArdle S，Endo S，Aspuru-Guzik A et al. arXiv：1808.10402

[53] Farhi E，Goldstone J. arXiv：1411.4028

[54] Temme K，Bravyi S，Gambetta J M. Phys. Rev. Lett.，2017，119：180509

[55] Endo S，Benjamin S C，Li Y. Phys. Rev. X，2018，8：031027

[56] Kandala A et al. Nature，2019，567：491

[57] Song C et al. arXiv：1812.10903

[58] McArdle S，Yuan X，Benjamin S. Phys. Rev. Lett.，2019，122：180501

[59] Bonet-Monroig X，Sagastizabal R，Singh M et al. Phys. Rev. A，2018，98：062339

編輯：黃飛

?