《射頻微波芯片設計》專欄適用于具備一定微波基礎知識的高校學生、在職射頻工程師、高校研究所研究人員,通過本系列文章掌握射頻到毫米波的芯片設計流程,設計方法,設計要點以及最新的射頻/毫米波前端芯片工程實現技術。
本文共計五部分
1.前言——討論為啥要學奇偶模分析功分器
2.答疑——對上一期《詳解集成電路中MOS管的基本原理和工作特性》的疑問解答
3.淺析——采用奇偶模對Wilkinson功分器分析
(全文閱讀大概需8分鐘,希望本期內容對您開卷有益)
前言
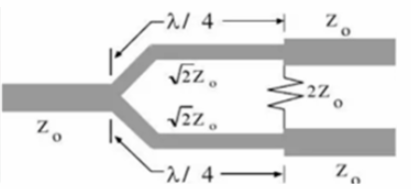
可能看到本期的標題大家就會想說,拋磚老師這功分器有啥好講的嘛,不就是兩根線條條+串一個小電阻就完事,還沒我晚上去吃夜宵擼的串的花樣多,這難道還能講出一朵花來?而且我看好多公眾號已經講過了啊,拋磚老師你再不講講高端點的芯片設計,我可要取關報警了!
且慢,其實,,,這個功分器呢,和我們之前講到的濾波器,耦合器,天線(更多內容可以點擊上方的文集列表去查看)一樣,也是我們射頻無源電路中的一個狠角色,在我們的射頻電路中可有著不低的地位,比如說在相控陣系統中多通道是不是需要咱門的功分器出馬,平衡式放大器是不是得他來做壓艙石,還有混頻器里的本振鏈路信號均分等等都有著她的倩影:
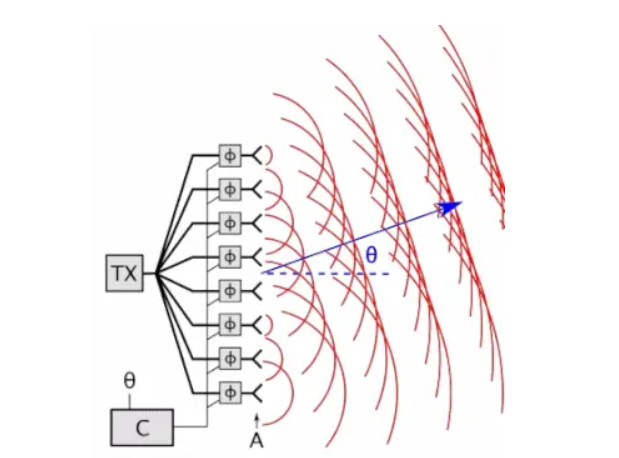
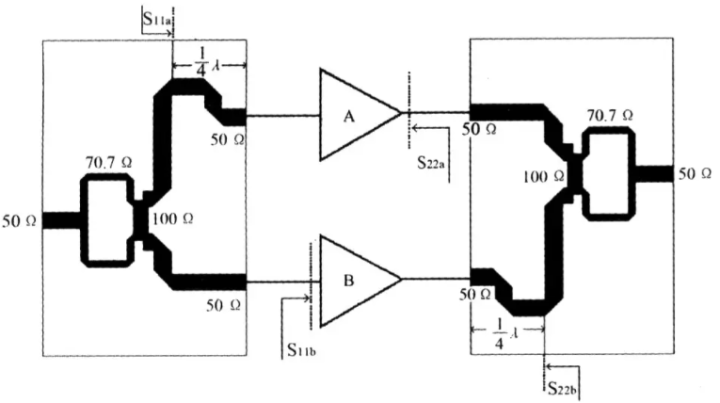
等等,,,我說拋磚老師,請不要轉換概念,我說的是這玩意挺簡單的,沒說他不重要,這么簡單的,是不是就沒有必要講了?
這。。。
那行,我先問大家3個關于Wilkinson功分器的問題,如果大家能1分鐘之內快速回答出來,那么也就沒有必要再浪費幾分鐘時間看后面的內容了:
Wilkinson功分器的隔離電阻是100歐姆,那為啥不是150,250?
Wilkinson功分器中的1/4波長線的阻抗,為什么是根號2倍特征值抗?
Wilkinson功分器的S參數矩陣是啥?
好了,大家先思考思考,如果心里有這三連的答案了,就大可跳過此篇文章,如果還是那種似是而非,說不出個所以然來的話,那我們可以接著往下看。
答疑
在采用奇偶模分析法去分析Wilkinson功分器之前,我們先對上一期《詳解集成電路中MOS管的基本原理和工作特性》里面的一個小問題進行答疑,這里主要分兩點:1.對網友的質疑提出回復;2.對上期我們出的考題給予回應。
1.對網友的質疑的回復
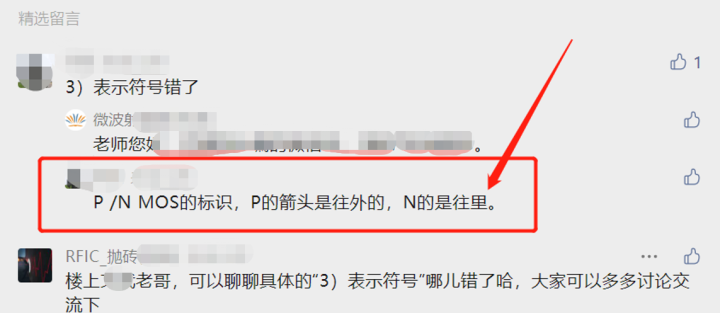
首先非常感謝該網友提出質疑,因為只有不斷交流,很多知識才可以內化成自己的東西,就比如今天我們敞開心扉聊一聊這個P/N MOS的符號問題,如果這個網友看到了今天這篇文章,我相信他對這個知識點可以記憶深刻,以后在遇到類似的問題就會一點就通,因此鼓勵大家多多提出自己的想法,多多交流,也可進群去和里面個個是人才說話有好聽的老哥們侃大山,聊技術、職業規劃、行業八卦等等。好了,閑話我們少扯,我們先把視線拉回上一期3)中的符號表達式:
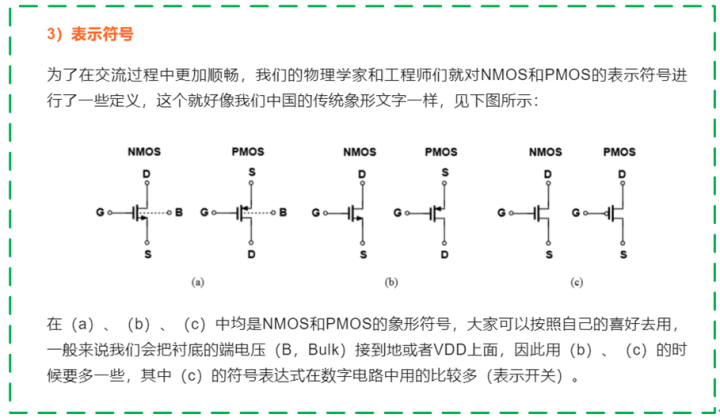
矛盾點在于:在上一期,我們說到了(a)、(b)兩種表達方式的N管符號箭頭朝外,P管反之;但是網友提到的是,N管應該朝內,P管反之。
那到底拋磚老師錯了,還是網友對了?這,其實兩者都沒毛病,但是呢,且看上期提到的反相器的原理圖和版圖:
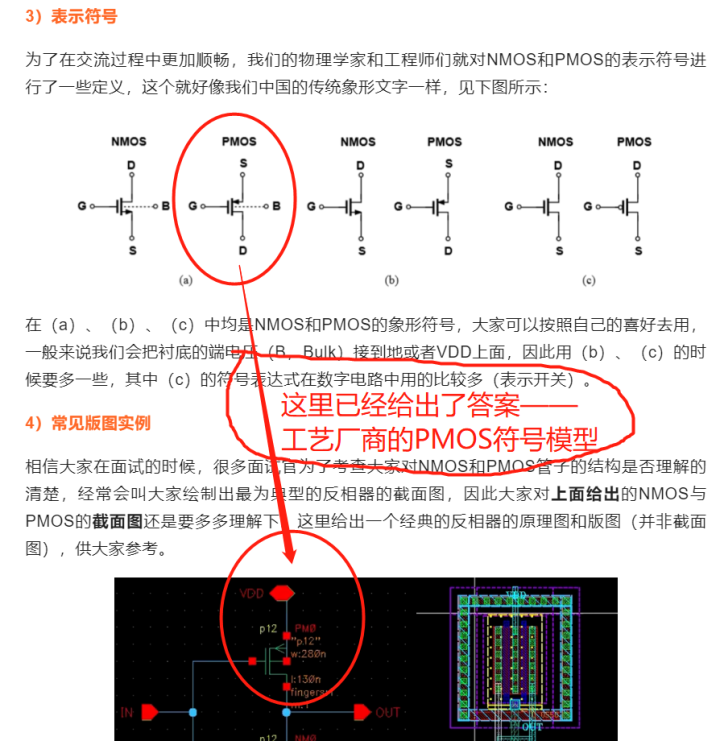
根據觀察,我們不難發現在現代工藝廠商,NMOS的箭頭都是朝外,可是,此時又有網友說了,拋磚老師,我從小接受的教育不允許我撒謊,我以前學模電的時候,老師說NMOS符號箭頭是朝內的,其實您說的對,之前的教材好多都是如此:
那么之所以有這個矛盾,個人理解是在于看我們把箭頭看成什么了,之前真空管過渡到固態電路的時候,我們往往還在聊載流子的走向,如果是NMOS管,那么我們源端(S)是給溝道提供載流子的,那么作為載流子的電子是朝著里面溝道流向的,換句話說,雖然電子是朝里但電流其實是朝外的,所以看似不同的表達,實則殊途同歸。
上面的NMOS、PMOS的符號指向問題就講到這里了,大家多活學活用,靈活處理各類小細節,這期繼續給大家一個小思考題,上一期我們3)符號的表達里面的PMOS的源極(S極)為什么要標識在下面藍色框框的位置???
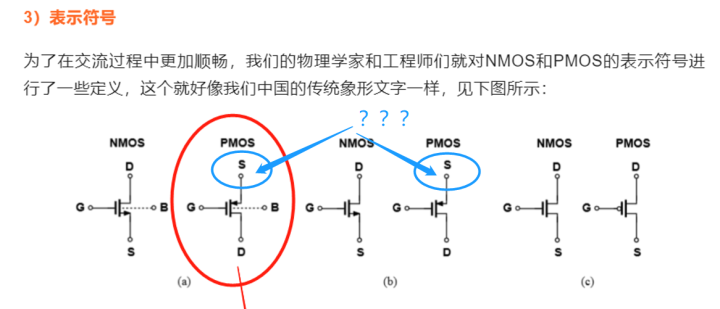
2.上期內容提出的小問題的解答
在上一期,我們提出了這樣一個簡單的問題,不知道大家有沒有答案了呢?
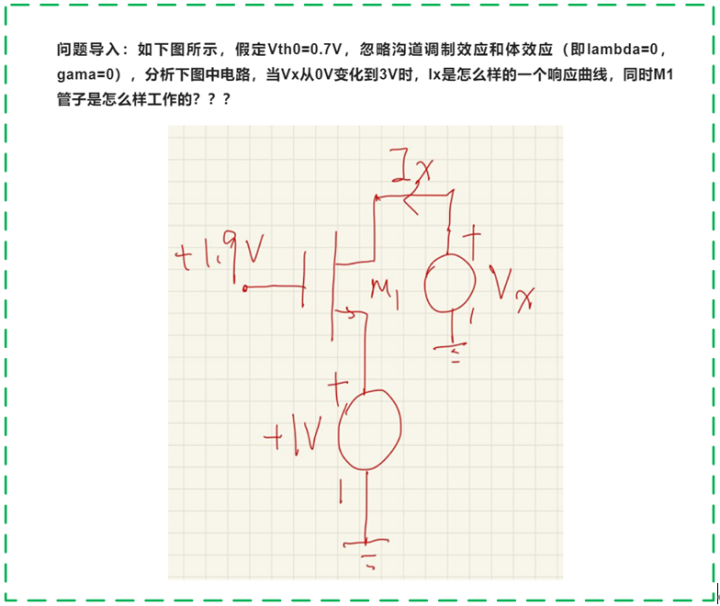
第一種情況:當Vx的電壓為0~1V時,此時的D/S反向,即Ix的電流流向為負數(箭頭反方向),此時M1處于線性區;
第二種情況:當Vx的電壓為1~1.2V時,此時的D/S再次互換,即Ix的電流流向為正數(箭頭方向),此時M1處于線性區;
第三種情況:當Vx的電壓為1.2~3V時,此時M1處于飽和區;
具體解答過程如下所示

奇偶模法分析功分器
就如我們第2期《芯片濾波器設計》談到的耦合矩陣法去設計濾波器、第7期《詳解基于ADS的低噪聲放大器芯片設計》談到的最小噪聲匹配法以及噪聲消除法去設計低噪放一樣,每一個射頻微波器件設計都會有一些自身比較有特殊的分析方法去進行設計。說到奇偶模分析法,這或許是射頻微波人應該、也是盡可能需要掌握的分析方法之一吧,要不然咱可真就成軟件的優化大師奴隸咯,即便工作多年,依舊會時不時陷入精神內耗。。。
那么,為什么要用奇偶模法來分析功分器呢?又是如何來利用奇偶模分析功分器?
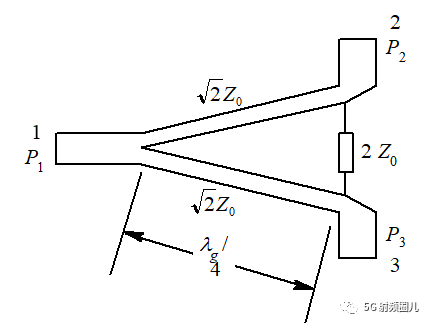
為了解答這個問題,我們先把視線調整回Wilkinson功分器的基本結構中來,如下圖所示,Wilkinson功分器是由對稱的上下兩支路構成,是一個典型的3端口器件:
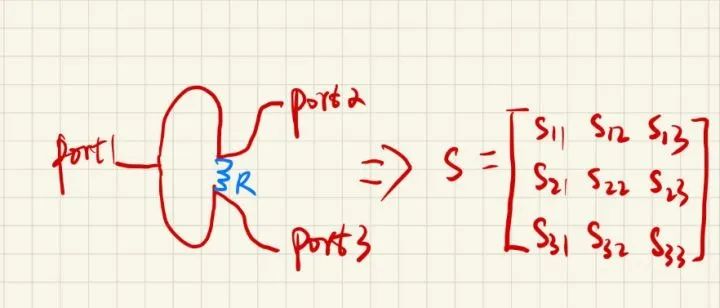
如果純粹地按照上面的S參數矩陣去硬分析,大兄弟,咱們怕是就go die了,不是說分析不了,確實是有點復雜了,因此我們在射頻微波電路的設計中,為了簡化分析模型,常常會采用基于對稱軸,進行分析的奇偶模法來分析微波電路的傳輸特性。
本文中的功分器中我們就是為了減小分析的復雜度,分別采用奇與偶模去得到相關參數,最后推導出整體電路的S參數,這樣分方法在有源電路里面同樣適用,比如用差模共模法去分析差分電路,當然用理想的電壁和磁壁去分析對稱的矩形波導結構也是不在話下的。
言歸正傳,我們怎么去分析如下圖所示的Wilkinson功分器呢?(大家在看《微波工程》或者網上其他資料,如果還有點疑問的話,那么現在請跟上拋磚的節奏,咱們爭取3分鐘內解決戰斗)
第一步:
先要明白,我們干這么一件事情的目的是什么:基本的需求就是求解在使得各個端口匹配的情況下,用精簡的分析模型去分析其網絡響應關系(可以換句話說,我們怎么求Wilkinson功分器的S參數矩陣)。
好了,有了上面的問題作為分析的大前提,我們現在又要搞清楚一個問題:如何去求解射頻微波網絡的S參數矩陣的?
這個就是基礎性的東西,求解S參數,我們無外乎就是在一個端口加激勵,然后去看想要觀察的端口的響應。比如我們常常所說的S21,那就是在1端口加激勵,2端口去看響應。
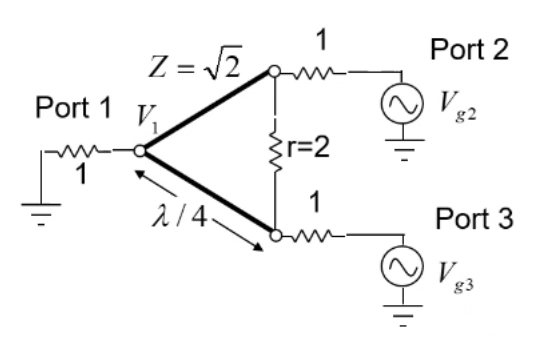
那么我們令端口2和端口3的信號大小分為:
Vo2=1/2*(Ve+Vo)
Vo3=1/2*( Ve-Vo)
然后我們想辦法,利用線性疊加原理,求解出在端口1的響應電壓,然后我們就可以得到相應的S參數矩陣。好了,大概的思路有了之后,我們開始對Wilkinson功分網絡進行分解。
第二步:
根據Wilkinson功分網絡的對稱性,首先我對傳輸線的特征阻抗,端口阻抗進行歸一化處理(方便后面我們寫算式),然后我們在中心對稱軸對其進行剖分,得到如下所示電路:
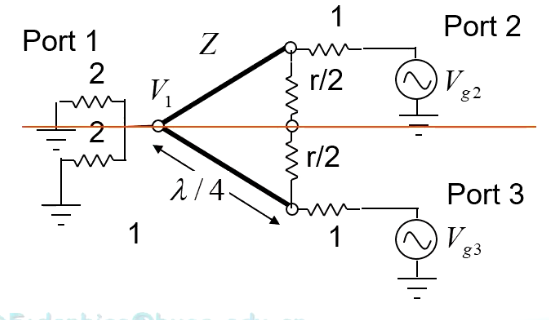
第三步:
我們分別來對奇模、偶模的情況,對電路進行拆分,方便后續進行相應的分析。
對于偶模而言,我們對端口2和3分別饋入2V0的電壓(即令Vg2=Vg3=2V0),此時由于2,3端口電位一樣,即可得到電路分析模型如下:
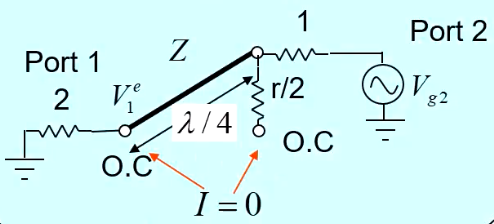
對于奇模而言,我們對端口2和3分別饋如V0的電壓(即令Vg2=-Vg3=2V0),此時得到如下的電路:
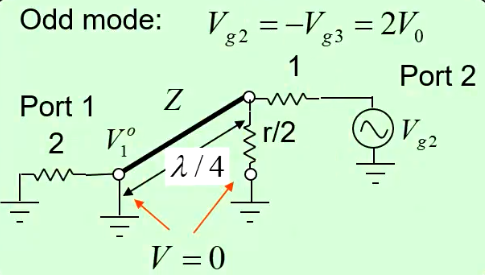
第四步:
針對第三步中的電路模型,我們分別給出奇偶模模型對應電路端口相應的傳函響應。
對于偶模,我們對其假設了端口2的電壓為2V0(端口三與其相同,又是對稱的,所以我們只要分析出2的激勵情況,對于端口3的情況一目了然)

此時端口2的歸一化內阻為1,對于中間的隔離電阻,此時處于開路狀態,因此可以對其忽略,為了讓端口2處于匹配狀態,在上圖1點往左看的電阻應該為1,對于一個1/4波長阻抗變換器,端口1的電阻又為2,那么為了實現良好匹配,1/4波長的特征阻抗
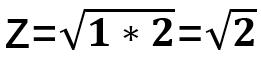
,說完阻抗,那么對于端口2的激勵到了端口1又是怎么樣的呢?此時我們可以把1/4波長傳輸線的ABCD矩陣給求出來,然后,我們可以把端口2那個位置的電壓通過ABCD矩陣轉換到端口1處,對于一個傳輸線的ABCD矩陣實際上是十分簡單的:
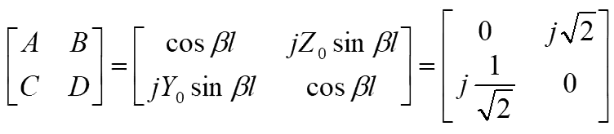
所以,此時我們可以得傳輸線兩端的轉換關系:
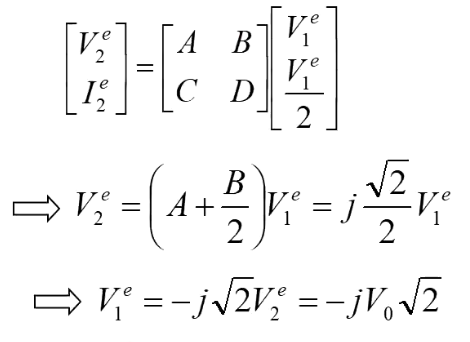
由于端口2與端口3完全對對稱的,所以此時:
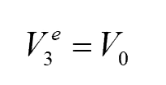
(題外話:讀到這里大家應該就可以明白為啥我們要假設Vg2和Vg3的電壓為2V0了吧,主要還是考慮到分壓情況,使得在傳輸線后的端點處的電壓為V0,這樣我們分析是的解析式更加簡潔方便一點,當然這是上帝視角,是站在已知結果的基礎上的假設,大家假設其他值也是完全沒有問題的)
對于奇模,我們對其假設了端口2的電壓為2V0,端口3的電壓為-2V0:

由于在輸入口的端點短路接地,即
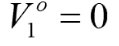
經過1/4波長傳輸線變換,就成了開路,此時在傳輸線右端點的電阻無窮大,因此port2為了匹配,r/2的值就應該等于port2的阻抗值,即r/2=1,即此時r=100Ω(大家應該清楚為啥是100歐姆了吧),
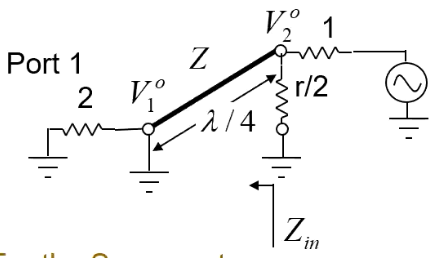
然后我們繼續把端口2(port2)的電壓分壓到傳輸線的右側端點,即:
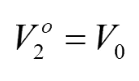
所以此時端口3下方,在傳輸線右側端點的電壓:
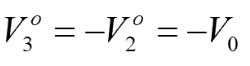
第五步:
根據上面求得的端點電壓,然后根據線性疊加原理,我們可以求得S參數的具體值,并最終得到S參數矩陣:
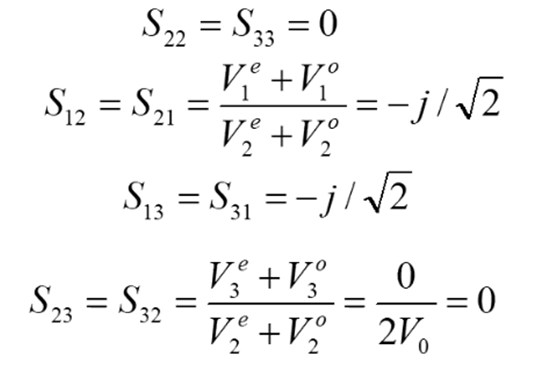
即,此時
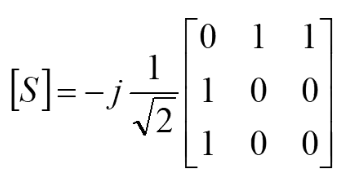
好了,到目前為止我們就完成了對Wilkinson功分器的分析,相信大家對隔離電阻取值,傳輸線特征阻抗的認識稍微加深了一點,如果還有什么不明白的,歡迎加入微波射頻網的交流溝通的群。
審核編輯:湯梓紅
 電子發燒友App
電子發燒友App























評論