愛好者在購買新的揚聲器單元時，往往會發現揚聲器單元制造商推薦有最佳的箱體尺寸。這方面可能包括密閉箱，開口箱的體積。通常，這個值與VAS或錐盆支撐順性的等效空氣容積有關，該順性是由錐盆和音圈質量，以及稱為揚聲器單元支撐的折環和定心支片的
剛性等幾個方面組成的。

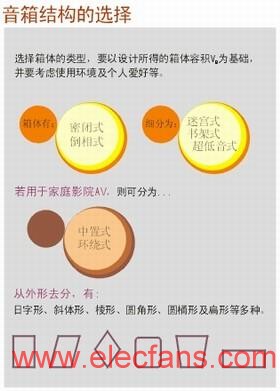
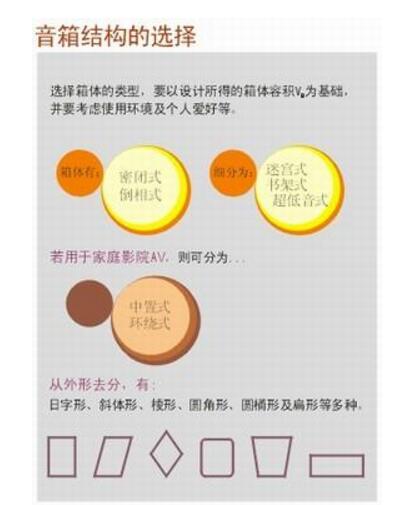
????（一）箱體的比例
????當愛好者制作揚聲器箱體時，有各種不同的結構選擇包括從立方體，圓管形，或矩形到許多其它的形狀。每種形狀都有特殊的特性、
優點和缺陷。但是，常用的音箱不管是閉箱還是倒相箱大都是長方形的箱體，所以，本文就是對長方形箱體尺寸關系進行的討論。

????假定揚聲器特性表中建議箱體容積Vb為0.09056立方米。愛好者就能用這個值為實際揚聲器單元確定理想的箱體尺寸了。如容積已定，先要把所要求的內部容積的立方米單位轉換為立方厘米，然后再求得結果的立方根，就可以得出所要求的高度、寬度、厚度了。正方形箱體（即高度、寬度、厚度相同的箱體）對用于超低音箱是很滿意的，因為這種箱體能通過增強內部駐波而提升箱體的總輸出。許多市售的超低音箱都是按這種樣子設計的。但是，本文的用意并非是用于超低音箱的，而是能覆蓋全音頻范圍的兩分頻或三分頻的音箱。

????通過實踐，許多音箱制造商已經采用了靠經驗得到的“黃金”比率或“黃金”分割率，這個比例或比率與根據理想比率0.618而確定的箱體尺寸比有關。舉例來說，應用的是整數尺寸，如6單位的深度，10單位的寬度，16單位的高度，深度對寬度的比率＝6：10＝0.60，而寬度對高度的比率＝10：16＝0.625，這些最終尺寸的縱橫比與理想的0.618值相當接近的，因為該比率可使選出的近似尺寸不會出現增強內部共振的公共簡正頻率，所以這個比率已被確認為能產生最佳的聲音。

????（二）計算內部尺寸
????假定所要求的內部純容積為0.0864立方米，計算過程如下：
1、?把0.09056立方米轉換為90560立方厘米。
2、?假定取縱橫比為6：10：16，將這三個數相乘，得到積為960。
3、?把總立方厘米90560除以960，得到的商為94.3。
4、?現在，求出94.3的立方根，大約為4.55。
5、?最后，用4.55乘以縱橫比的三個值，分別為，6×4.55＝27.3（厚度），10×4.55＝45.5（寬度），而16×4.55＝72.8（高度）。
6、?經過這些計算，將箱體的寬度、高度和厚度值相乘，和原來要求的箱體容積90620cm3相比較。由于要化為整數，乘積可以稍有不同，????當有1％誤差時可以認為是無關緊要的。

????以上就是決定箱體最佳尺寸的全過程。作為例子，讀者也能選擇其他的7：11：17縱橫比，或34：55：89而且按前面舉例的同樣方法進行。當最佳值有5％左右誤差時，對放音質量僅有很小的影響。

????（三）關于誤差
????假如讀者遇到的是小容積的音箱，那么此時容積是與揚聲器單元裝在箱內占有的容積有關的。讀者可以把箱體容積做得稍為大些以補償揚聲器單元的容積。假如在揚聲器單元特性中沒有給出揚聲器單元的位移值,那么可以根據下述公式計算近似的位移值（或容積）：V＝πr?2h?，式中，r是磁體半徑，而h是磁體的厚度或高度。設磁體直徑為11.4cm(半徑就是5.7cm)，厚度為2.5cm，容積為：3.1416×5.7?2?×2.5=255.2cm3??現在，計算用下面公式計算錐盆容積：V=πr2h?／3設錐盆直徑為22.9cm，而高度為5.1cm，所以錐盆容積為:?3.1416×11.52?×5.1?／3＝706.3cm3把磁路容積（255.2cm3）與錐盆容積(706.3cm3)相加，給出揚聲器單元容積為961.5cm3。該值只不過比箱體所要求容積90560cm3的1％稍大些而已。所以在這種情況下揚聲器單元的容積是并不重要的。只要揚聲器單元的合成容積不超出總箱體容積的5％，在計算時就可以忽略不計了。

????無論讀者用什么樣的比例，深度、寬度和高度的尺寸都不應該存在任何一個數的整倍數。舉例說來,不應該采用8，16和24，因為這些數都是8的整倍數，所以在箱內將會出現有害的共振。

????對超低音箱來說，因為這種箱需要共振，所以常常制成正方形的。而且，這種音箱放音僅覆蓋較窄的頻段，故而箱體的共振增強了輸出。當然，也能利用開口箱形式進一步增強低音。

????（四）數學上的黃金切割率
????表示黃金切割率的數(也稱為黃金平均值，黃金比例和黃金分割)是從劃分線段得出的。此時較短的部分對較長的部分之比等于較長的部分對線段總長之比值（圖1）。設線段總長度為1，且取較長部分為x，那么較短的部分就是1-x，這樣導出的比率就是：?
[（1-x）／x]＝（x／1）或?x2＝1-x?（1）稍經排列,可給出一元二次方程：x2＋x－1＝0?（2）
將此式與二次方程基本形式比較，可得ax2+bx+c=0,且應用該公式，x=(-b?)/2a?x的正值（較長的線段）可得0.61803…，作為實際應用四舍五入為0.618。通過相減，較短部分的長度即為0.382，正如方程（1）直接顯示那樣，該值是較長線段的平方。

????讀者還可以（在理論上）找到一個通過幾何結構分割而得到的正確的分割點。在圖2上，ABC是一個直角三角形，為方便起見，選擇AB為2單元，而BC（垂直于AB）選定為1，根據勾股定律，AC＝。以C為圓心，半徑＝BC＝1作圓弧，交于斜邊上D點，得AD＝-1。再以A為圓心，AD為半徑作圓弧，交AB于G點，該點即為分割AB的黃金比率。較長部分AG＝-1，而較短的部分GB＝2－(-1)=3-。應用這些值，我們能夠看出?
GB／AG＝AG／AB是相同的。

?????黃金比值也能從其它數學運算中得到。例如，有一種費班納賽序列（FIBONACCI?SERIES），這種數制序列中每個數等于前面兩個數的和）：1，2，3，5，8，13，21，34，55，89，144，233，377，等等。稍作驗算，數序怎樣建立就清楚了，取連續的一對數的比率看其結果：
1：1＝1；1：2＝.5；2：3＝.67…；3：5＝.6；5：8＝.625；8：13＝.61538…；13：21＝.61904…21：34＝.61764…；34：55＝.61818…；等等。

黃金比率在許多方面都有出現，例如，正五邊形對角線的線段，在測量五個正幾何立體金字塔的一定比率，而最顯著的是在自然界中，假如讀者能獲得一個大的成熟的向日葵，請注意花簇頭部的順時針和逆時針方向的螺旋紋，仔細數出兩個方向的螺紋數，取較小的數和較大的數的比率，再和Fibonacci數序的比率比較。

?????顯然，這是一個值得注意的比率，而且當引入到揚聲器箱體尺寸后，揚聲器箱放音非常優良就沒有什么奇怪了。