無人車作為一個復雜軟硬件結合系統，其安全可靠運行需要車載硬件、傳感器集成、感知預測，以及控制規劃等多個模塊的協同配合工作。作者認為最關鍵的部分是感知預測和決策控制規劃的緊密配合。狹義上的決策規劃控制部分，包含了無人車行為決策（Behavior Decision）、動作規劃（Motion Planning）， 以及反饋控制（Feedback Control）這三個模塊。而從更寬泛的概念來說，無人車的決策規劃控制模塊，緊密依賴于上游的路由尋徑（Routing）以及交通預測（Prediction）的計算結果，所以本文也對路由尋徑和交通預測模塊進行介紹。

　　系統框架和模塊劃分

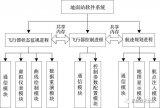
　　圖1展示了一種無人車軟件系統的典型功能模塊劃分。其中感知（Perception）模塊負責從傳感器數據中探測計算出周邊環境的物體及其屬性。這些物體信息經過預測模塊的計算，生成預測軌跡傳遞給決策規劃控制系統中的行為決策模塊。決策規劃控制系統的另一個上游模塊是路由尋徑模塊，其作用在簡單意義上可以理解為無人車軟件系統內部的導航，即在宏觀層面上指導無人車軟件系統的控制規劃模塊按照什么樣的道路行駛從而實現從起始點到目的地點。值得注意的是這里的路由尋徑雖然在一定程度上類似傳統的導航，但其細節上緊密依賴于專門為無人車導航繪制的高精度地圖，所以和傳統的導航還是有本質的不同。一般來說，路由尋徑會作為單獨的模塊來進行實現，而交通預測部分，則既可以做為感知模塊的業務延伸，也可以看成是決策規劃控制模塊的外圍模塊而單獨進行實現。

　　圖1 無人車軟件系統模塊

　　決策規劃控制（Decision，Planning & Control）系統的任務，就是在對感知到的周邊物體的預測軌跡的基礎上，結合無人車的路由意圖和當前位置，對車輛做出最合理的決策和控制。整個決策規劃控制軟件系統，可以按照解決問題的不同層面，如圖1所示自上而下劃分為行為決策（Behavioral Decision）、動作規劃（MotionPlanning），以及反饋控制（Feedback Control）這三個模塊。

　　其中行為決策模塊（Decision），可以直觀理解成無人車的“副駕駛”。行為決策接受路由尋徑的結果，同時也接收感知預測和地圖信息。綜合這些輸入信息，行為決策模塊在宏觀上決定了無人車如何行使。宏觀層面的決策包括在道路上的正常跟車，在遇到交通燈和行人時的等待避讓，以及在路口和其他車輛的交互通過等。例如，在路由尋徑要求無人車保持當前車道（Lane）行駛，感知發現前方有一輛正常行駛的車輛，行為決策的決定便很可能是跟車行為。 動作規劃模塊，在圖1的劃分中，解決的是具體的無人車動作（Motion）的規劃問題。其功能可以理解為，在一個較小的時空區域內，具體解決無人車從A點到B點如何行駛的問題。動作規劃模塊在這里解決的問題，相對行為決策，又更加具體了一步。動作規劃需要具體把一個短暫時間t內從A到B的中間路徑點做出規劃，包括選擇途經哪些具體的路徑點，以及到達每個路徑點時，無人車的速度，朝向，加速度等。不僅如此，動作規劃還需要保證兩點：一是在后續時間內，生成從A到B的時空路徑需要保持一定的一致性；二是，這些生成的A到B之間的路徑點，包括到達每個點的速度朝向加速度等，都在下游的反饋控制的實際可操作的物理范圍之內。決策規劃控制系統最下層的模塊是反饋控制模塊。這是一個直接和無人車底層控制接口CAN-BUS對接的模塊。其核心任務是消化上層動作規劃模塊的輸出軌跡點，通過一系列結合車身屬性和外界物理因素的動力學計算，轉換成對車輛Drive-By-Wire控制的油門，剎車，以及方向盤信號，從而盡可能地控制車去實際執行這些軌跡點。反饋控制模塊主要涉及對車輛自身控制，以及和外界物理環境交互的建模。

　　上述模塊的劃分方法，非常有效地將無人車決策控制規劃這樣一個復雜問題，按照計算邏輯從抽象到具體的做出了非常合理的切分。這樣的劃分使得每個模塊可以各司其職專注解決本層次的問題，從而提升了整個復雜軟件系統的開發效率。

　　預測模塊（Prediction）

　　作為決策規劃控制模塊的直接數據上游之一，預測模塊的作用是對感知所探測到的物體進行行為預測，并且將預測的結果具體化為時間空間維度的軌跡傳遞給下游模塊。一般而言，感知模塊所輸出的物體信息包括位置，速度，朝向以及物體分類（如車輛，行人，自行車）等物理屬性。這些感知所計算輸出的物體屬性偏向于客觀的物理屬性。利用這些輸出的屬性，結合客觀的物理規律，可以對物體做出一個在非常短時間內的“瞬時預測”。預測模塊所需要解決的問題，不僅僅局限于結合物理規律對物體做出預測，往往更重要的是結合物體和周邊環境，以及積累的歷史數據知識，對感知到的物體做出更為宏觀的行為預測。例如在圖2中，行為預測需要在宏觀層面預測圖中的車輛是否會保持直行還是右轉通過路口。

　　圖2 無人車周邊物體行為預測

　　行為預測的軌跡，既包括了障礙物在將來一段時間內運動的方向，還體現了它們在運動中的速度變化。譬如行人過馬路的時候會預測他們使用較為恒定的步行速度，車輛轉彎的時候會先減速后加速，而加減速的快慢也取決于彎道的弧度和長短。實際的無人車系統中，往往將宏觀層面的行為預測和軌跡生成抽象成兩個問題來解決。

　　宏觀層面的行為預測問題，往往可以抽象成經典的機器學習問題，并且利用基于大數據的深度學習技術來解決。例如， 在假設車輛按照高精地圖劃分的道路（Lane）行駛的前提下，我們可以認為在任何一個時刻，車輛可行駛的每一個Lane序列都是一個需要進binary classification的樣本。在這個假設下，我們不需要對直行、并道、路口拐彎等場景進行區分處理，因為無論是直行、并道，和路口拐彎，都可以統一看成是車輛在不同Lane序列上的行駛。車輛的宏觀行為預測問題，變簡化為對于Lane序列的Binary Classification問題。

　　圖3 無人車行為預測中的Lane序列Binary Classification抽象

　　如圖3所示，在t時刻，無人車主車位于Lane 1，此時按照Lane序列的可能展開途徑，我們考慮三條軌跡：

　　· Trajectory 1： Lane 1、Lane 2、Lane 3對應路口右轉；

　　· Trajectory 2：Lane 1、Lane 6、Lane 8對應路口直行；

　　· Trajectory 3：Lane 1、Lane 4、Lane 5、Lane7對應換道后直行通過路口。

　　假設在t+w時刻，無人車經過Lane 6行駛到Lane8的位置，那么軌跡Trajectory 2便成為該Binary Classification的正樣本，其余兩條軌跡便成為負樣本。在這種基于Lane序列的問題抽象下，所有的正負樣本可以從歷史數據的回放中獲得，并成為模型訓練的樣本數據。另一方面，模型的特征抽取可以結合一定時間內的如下信息來設計：

　　· 車輛本身的物理信息：速度、朝向等；

　　· 車輛相對于道路的信息：在Lane上的橫向/縱向位移和速度，相對Lane邊界的距離等；

　　· 車輛周邊的其他物體的信息：車輛周圍例如左右相鄰Lane是否有障礙物等。

　　在上述的樣本標簽定義和特征抽取下，無人車Prediction部分的宏觀行為預測可以很好的抽象成典型的機器學習問題來解決。在預測得出的宏觀行為基礎上，相關的軌跡生成和速度預測可以通過特定的規則或者物理模型來實現。

　　路由尋徑（Routing）

　　無人車路徑規劃的Routing尋徑問題，雖然也是要解決從A點到B點的路由問題，但由于其輸出結果并不是為實際的駕駛員所使用，而是給下游的行為決策（Decision）和動作規劃（Planning）等模塊作為輸入，其路徑規劃的層次要更加深入到無人車所使用的高精地圖的車道（Lane）級別。如圖4所示，其中的箭頭線段代表高精地圖級別的道路劃分和方向。lane1，lane2，………，lane8構成了一條Routing輸出的路由片段序列。可以看到，無人車地圖級別的Lane劃分并非和實際的自然道路劃分對應。比如lane2，lane5，lane7都代表了由地圖定義繪制的“虛擬”轉向Lane。類似的，一條較長的自然道路，也可能被劃分為若干個lane（例如lane3，lane4 ）。

　　做為整體無人車決策控制規劃（Decision，Planning & Control）系統的最上游模塊，路由尋徑模塊的輸出嚴格依賴于無人車高精地圖（HD-Map）的繪制。在高精地圖定義繪制的路網（Road Graph）的道路（Lane）劃分的基礎上，以及在一定的最優策略定義下，路由尋徑模塊需要解決的問題是計算出一個從起點到終點的最佳道路（Lane）行駛序列：{（lane，start_posotion，end_position）i}，其中，（lane，start_posotion，end_position）i我們稱作一個Routing Segment（路由片段），所在的道路由lane來標識，start_posotion，end_position分別代表在這條道路上的起始縱向距離和結束縱向距離。

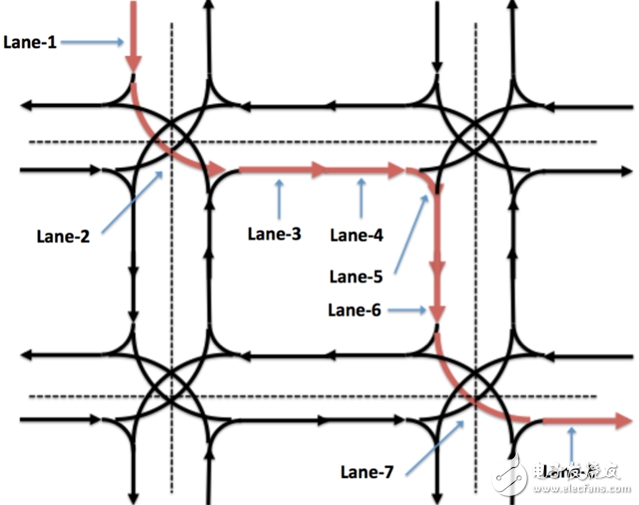
　　圖4 無人車路由尋徑模塊（Routing）的高精地圖道路（Lane）級別尋徑路由

　　圖5 無人車尋徑（Routing）基于Lane Point的有向帶權圖上的最短路徑問題抽象

　　我們可以把無人車在高精地圖的Lane級別尋徑問題，抽象成一個在帶權有向圖上的最短路徑搜索問題（如圖5所示）。路由尋徑（Routing）模塊首先會基于Lane級別的高精度地圖，在一定范圍內所有可能經過的Lane上進行分散“撒點”，我們稱這些點為“Lane Point”。這些點代表了對無人車可能經過的Lane上的位置的抽樣。這些點與點之間，由有向帶權的邊進行連接。Lane Point之間連接的權，代表了無人車從一個點行駛到另一個點的潛在代價（Cost）。在這樣的有向帶權圖的問題抽象下，路由尋徑問題可以利用常見的A*算法或者Dijkstra算法來進行實現。

　　行為決策（Behavioral Decision）

　　行為決策（Behavior Decision）層在整個無人車決策規劃控制軟件系統中扮演著“副駕駛”的角色。這個層面匯集了所有重要的車輛周邊信息，不僅包括了無人車本身的當前位置、速度、朝向以及所處車道，還收集了無人車一定距離以內所有重要的感知相關的障礙物信息以及預測軌跡。行為決策層需要解決的問題，就是在知曉這些信息的基礎上，決定無人車的行駛策略。這些信息具體包括：

　　所有的路由尋徑結果：比如無人車為了達到目的地，需要進入的車道是什么（target lane）。

　　· 無人車的當前自身狀態：車的位置速度朝向，以及當前主車所在的車道。

　　· 無人車的歷史信息：在上一個行為決策（Behavioral Decision）周期，無人車所做出的決策是什么？是跟車，停車，轉彎或者是換道？

　　· 無人車周邊的障礙物信息：無人車周邊一定距離范圍內的所有障礙物信息。例如周邊的車輛所在的車道，鄰近的路口有哪些車輛，它們的速度位置如何？以及在一個較短的時間內它們的意圖和預測的軌跡。周邊是否有自行車或者行人，以及他們的位置速度軌跡等；

　　· 無人車周邊的交通標識信息：一定范圍內的Lane的變化情況。比如路由尋徑的結果是在Lane1的縱向位移10m處換道進入對應的相鄰Lane2的縱向位移20m處，那么Lane 1的合法的縱向位移換道空間是多大？比如從一個直行Lane行駛結束，需要進入下一個左轉Lane，兩條Lane的交界處是否有紅綠燈或者人行道？

　　· 當地的交通規則：例如道路限速，是否可以紅燈右拐等等。

　　無人車的行為決策模塊， 就是要在上述所有信息的基礎上，做出如何行駛的決策。可以看出，無人車的行為決策模塊是一個信息匯聚的地方。由于需要考慮如此多種不同類型的信息以及受到非常本地化的交規限制，行為決策問題往往很難用一個單純的數學模型來進解決。往往更適合行為決策模塊的解決方法，是利用一些軟件工程的先進觀念來設計一些規則引擎系統。例如在DARPA無人車競賽中，Stanford的無人車系統“Junior”利用一系列cost設計和有限狀態機（Finite State Machine）來設計無人車的軌跡和操控指令。在近來的無人車規劃控制相關工作中，基于馬爾可夫決策過程（Markov Decision Process）的模型也開始被越來越多得應用到無人車行為層面的決策算法實現當中。簡而言之，行為決策層面需要結合路由尋徑的意圖，周邊物體和交通規則，輸出宏觀的行為層面決策指令供下游的動作規劃模塊去更具體地執行。其具體的指令集合設計則需要和下游的動作規劃模塊達成一致。

　　動作規劃（Motion Planning）

　　在行為決策層下游的模塊是動作規劃（Motion Planning）。其任務是具體將行為決策的宏觀指令解釋成一條帶有時間信息的軌跡曲線，來給最底層的反饋控制來進行實際對車的操作。更具體而言，動作規劃模塊試圖解決在一定的約束條件下優化某個范圍內的時空路徑問題。這里的“時空路徑”指車輛在一定時間段行駛的軌跡。該軌跡不僅包括位置信息，還包括了整條軌跡的時間信息和車輛姿態：即到達每個位置的時間，速度，以及相關的運動變量如加速度，曲率，曲率的高階導數等。動作規劃可以拆分成為兩個問題：軌跡規劃（Trajectory Planning）和速度規劃（Speed Planning）來解決。其中軌跡規劃只解決在二維平面上，根據行為決策和綜合地圖信息定義的某種Cost函數下，優化軌跡的問題；而速度規劃問題則是在選定了一個或者若干個軌跡（Trajectory）之后，解決用什么樣的速度來行駛的問題。xˉ=（x，y，θ，k，v），其中（x，y）表示車輛在二維平面的位置，θ表示車輛的朝向，k表示曲率（也即朝向θ的變化率），v表示車輛的速度（即軌跡任意點的切線速度）。車輛的這些姿態變量的標量大小滿足如下關系：

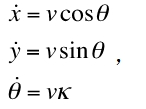
　　其中曲率的k大小往往由系統的輸入限制條件決定。在此基礎上，考慮一條由車輛運動產生的連續軌跡（Path）。我們稱沿著軌跡的方向的位移為S方向。軌跡相對于車輛姿態的系統關系由下列偏微分方程式給出：

　　我們的軌跡規劃（Trajectory Planning）算法非常依賴于地圖對于道路的定義。這里我們定義道路由其道路中心線（Center Line）所定義，且定義道路的采樣函數為：

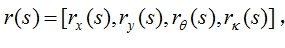　　，其中s代表道路的中心線切向方向的位移（也稱為縱向位移s）。于此對應的是道路的中心線垂直方向位移l，也稱之為橫向位移。如果考慮一個車輛的姿態點p點在道路上（s，l）坐標，那么其實際的姿態和（s，l）的關系滿足：

　　其中曲率Kr定義為在道路轉彎的內側曲率加大（隨縱向位移l加大），外側曲率則減小。我們使用右手坐標系，所以如圖6所示在靠近原點處朝x軸的正方向，縱向位移l朝著y軸正方向加大。假設對于某條道路Lane（k），其縱向寬度lk保持不變。那么該條道路變可以表示成為一個隨著中心線橫向位移s的點集{p（s，lk）：s∈R+}。我們稱這樣的一個坐標系統為坐標系統。

　　圖6 XY平面下的SL坐標系統及其網格劃分

　　在上述的車輛模型和道路模型下，我們討論軌跡規劃所產生的軌跡曲線。首先我們定義車輛的軌跡（Trajectory）為一個從［0，1］區間到車輛姿態向量集合C={x? }的連續映射：ρ：［0，1］→C 。其中，車輛的初始姿態向量為x? =（x，y，θ，k）。每條軌跡終點處如圖7所示，軌跡1的終點姿態為ρ1（1）=qend1軌跡2的終點姿態向量為ρ2（1）=qend2，初始姿態為ρ1（0）=ρ2（0）=qinit。軌跡優化的目標便是在所有可能的軌跡曲線中，篩選出滿足邊界條件的軌跡曲線，再尋找一條/若干條平滑且Cost函數最低的曲線。其中軌跡的候選曲線我們用類似在路由尋徑（Routing）模塊中介紹的“撒點”的采樣方式來生成。參考圖7，在某條Lane的SL坐標系下，我們按照均勻切分的S和L方向的方格內，在固定S和L間隔下，考慮每個（si，lj）區域的中心點（如圖7所示，又稱為軌跡點Trajectory Point）。一條候選的軌跡（Trajectory）便可以看做是沿著Lane的中心線縱向位移s方向連接不同Trajectory Point的平滑曲線。在圖7所示的道路SL分割和采樣下，可能的Trajectory Point有16個（4個s位置，4個l位置），從車輛的初始位置出發，我們只考慮在s方向單調增大的可能，不考慮城市綜合道路行駛中的倒車情況，那么總的候選曲線的總條數為44=256條。軌跡優化便是要在這256條候選的曲線中找出Cost最優的軌跡。

　　圖7 SL坐標系下道路的分割采樣以及可能的軌跡

　　我們采用多項式螺旋線來連接軌跡點Trajectory Point，從而生成候選的曲線。多項式螺旋線，如圖8所示，代表了一類曲率可以用弧長（對應我們軌跡中的s方向）的多項式函數來表示的曲線簇。我們使用三階（Cubic）或者五階（Quintic）的多項式螺旋線，其曲率K和軌跡弧長S的關系K（S）為：或者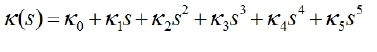

　　圖8 多項式螺旋線以及車輛姿態的螺旋線示意圖

　　基于這種使用三階（五階）螺旋線連接的軌跡（Trajectory），其參數可以快速有效的通過梯度下降（Gradient Descent）的方法來搜索。以三階多項式為例，我們考慮從車輛初始姿態qinit=（xI，yI，θI，KI）到目標姿態qgoal=（xG，yG，θG，KG），且具有連續曲率的三階螺旋線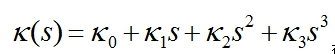：在初始狀態 時，考慮曲率的一階導數和二階導數均需要滿足初始狀態的限制，我們可以得到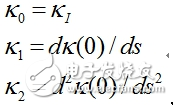：，這樣使得實際未知參數減少到2個（K3，SG），利用梯度向量我們可以快速尋找到非常接近初始狀態限制的三階螺旋線的參數。在上述的所有候選曲線中，我們可以根據業務的不同需要來設置Cost函數，然后選擇出在任何時間點Cost最小且滿足邊界條件限制的曲線。由于候選曲線隨著我們采樣間隔隨指數增長，往往將Trajectory Point建立成某種有向帶權圖，然后利用圖論中的搜索方法結合Cost設置來選取最優曲線。具體的搜索方法可以參考中的動態編程方法。

　　在軌跡規劃選定了一條或者若干條曲線后，速度規劃部分將決定車輛以什么樣的速度來通過這條曲線。軌跡規劃在選取曲線時的Cost設置偏重于靜態障礙物，而速度規劃在選取曲線時的Cost設置應該注意以下幾點：

　　· 動態的障礙物信息：如Prediction模塊預測的軌跡信息；

　　· 上游Decision輸出的宏觀層面指令：如對某個障礙物需要避讓（Yield）；

　　· 狀態量的連續性限制：如速度，加速度等均不能跳變。

　　在此基礎之上，速度規劃可以將曲線的縱向位移S和時間變量T建立一個二維平面，將上述的限制投影在該平面上求解這個問題。這種考慮曲線縱向位移s和時間t的速度規劃求解方式稱之為S-T求解。類似得，如果考慮橫向位移，也可以在三維的S-L-T空間內進行求解。

　　反饋控制（Feedback Control）

　　無人車反饋控制模塊中常用的車輛控制模型為自行車模型。在該模型中，車輛姿態（Pose）是處于一個二維的平面坐標系內，并且可以由車輛所處的位置（position）以及車身和坐標平面的夾角（heading）來完全描述。同時我們假設車輛前后輪由一個剛性（rigid）不變的軸連接，其中車輛的前輪可以在一定的角度范圍內自由轉動，而車輛的后輪保持和車身的平行關系不能轉動。前輪的轉動對應實際車輛控制中方向盤的轉動。

　　車輛的自行車模型所代表的車輛姿態如圖9所示。這里我們使用一個基于x-y的二維平面，其中e^x和e^y分別代表其x和y方向的單元向量。向量pr和向量pf分別代表車輛后輪和前輪與地面的接觸點。車輛的朝向角θ代表車輛和x軸的夾角（即向量pr和單元向量e^x的夾角）。方向盤轉角δ定義為前輪朝向和車輛朝向角的夾角。其中前后輪與地面接觸點的向量pf和pr之間滿足：

　　其中y˙f和y˙r分別代表車輛前后輪在和地面接觸點處的瞬時速度向量。考慮車輛的后輪速度在x-y軸的投影標量xr：=pr·e^x和xy：=pr·e^y以及后輪的切向速度，那么上述的向量pf和pr之間的關系限制在后輪相關分量上的表現形式為：其中 l代表車輛前后軸中心間距。類似地，用車輛前輪相關分量的表現形式為：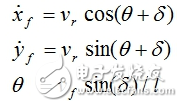

　　這里前后輪的切向速度標量大小滿足：

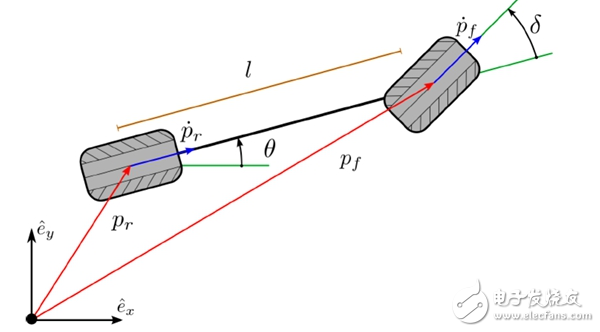
　　圖9 車輛控制的自行車模型

　　在上述的車輛模型下，反饋控制（Feedback Control）需要解決的問題便是找到滿足車輛動態姿態限制的方向盤轉角δ∈［δmin，δmax］的以及前向速度vr∈［δmin，δmax］。而對這些狀態量的控制可以是一個典型的PID反饋控制系統（如圖10所示）。其中e（t）代表當前的跟蹤誤差，而這個跟蹤的變量誤差可以是軌跡的縱向/橫向誤差，角度/曲率誤差或者是若干車輛姿態狀態變量的綜合誤差。其中P控制器代表對當前誤差的反饋，其增益由KP控制；I和D控制器分別代表積分項和微分項，其增益分別有KI和KD來控制。

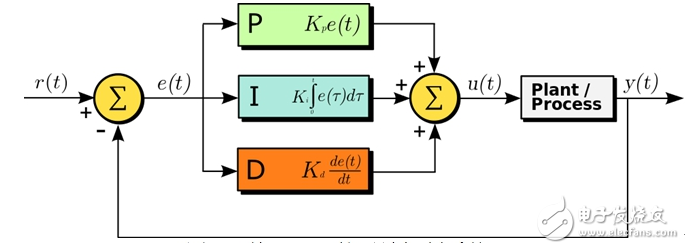
　　圖10 基于PID的反饋控制系統

　　具體到無人車的反饋控制（Feedback Control）模塊，我們需要解決的問題是控制車輛盡可能遵循上游動作規劃（Motion Planning）所輸出的時空軌跡。可以使用兩個基于PID反饋控制的控制器來分別控制方向盤轉角δ以及前進速度vs。