一、小波分析算法的計算

　　1、Mallat算法［經典算法］

　　在小波理論中，多分辨率分析是一個重要的組成部分。多分辨率分析是一種對信號的空間分解方法，分解的最終目的是力求構造一個在頻率上高度逼近L2（R）空間的正交小波基，這些頻率分辨率不同的正交小波基相當于帶寬各異的帶通濾波器。因此，對于一個能量有限信號，可以通過多分辨率分析的方法把其中的逼近信號和細節信號分離開，然后再根據需要逐一研究。多分辨率分析的概念是S.Mallat在構造正交小波基的時候提出的，并同時給出了著名的Mallat算法。Mallat算法在小波分析中的地位相當于快速傅立葉變換在經典傅立葉變換中的地位，為小波分析的應用和發展起到了極大的推動作用。

　　MALLAT算法的原理

　　在對信號進行分解時，該算法采用二分樹結構對原始輸入信號x（n）進行濾波和二抽取，得到第一級的離散平滑逼近和離散細節逼近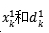，再采用同樣的結構對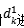進行濾波和二抽取得到第二級的離散平滑逼近和離散細節逼近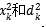，再依次進行下去從而得到各級的離散細節逼近對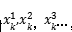，即各級的小波系數。重構信號時，只要將分解算法中的步驟反過來進行即可，但要注意，此時的濾波器與分解算法中的濾波器不一定是同一濾波器，并且要將二抽取裝置換成二插入裝置才行。

　　2、多孔算法

　　多孔算法是由M.shen于1992年提出的一種利用Mallat算法結構計算小波變換的快速算法，因在低通濾波器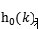和高通濾波器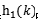中插入適當數目的零點而得名。它適用于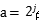的二分樹結構，與Mallat算法的電路實現結構相似。先將Mallat算法的電路實現的基本支路作一下變形。令的z變換為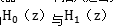，下兩條支路完全等價，只不過是將插值和二抽取的順序調換一下罷了。圖中其它的上下兩條支路也為等效支路，可仿照上面的方法證明。這樣，我們便可由Mallat算法的二分樹電路結構得出多孔算法的電路級聯圖，原Mallat算法中的電路支路由相應的等效支路所取代，所以整個電路形式與Mallat算法非常相似。如果舍去最后的抽取環節們實際上相當于把所有點的小波變換全部計算出來。

　　3、基干FFT的小波快速算法

　　Mallat算法是由法國科學家StephaneG.Mallat提出的計算小波分解與重構的快速算法，能大大降低小波分解與重構的計算量，因此在數字信號處理和數字通信領域中得到了廣泛的應用。但是如果直接采用該算法計算信號的分解和重構，其運算量還是比較大。主要體現在信號長度較大時，與小波濾波器組作卷積和相關的乘加法的計算量很大，不利于信號的實時處理。故有必要對該算法作進一步的改進。眾所周知，FFT是計算離散傅里葉變換（DFT）的一種快速算法，如能將它和Mallat算法結合在一起，勢必會進一步降低小波分解和重構的計算量，事實證明這一想法是可行的。

　　基于FFT的小波變換快速算法是通過離散傅里葉變換建立起FFT和mallat算法之何的橋梁，從而將、FFT引入到小波變換中來，達到改小波變換快速算法及硬件實現的研究進Mallat算法的目的。

　　當信號長度較小時，FFT算法效率不及直接算法;隨著長度的增加，特別是對于長度是2的幕次方的信號，FFT算法比直接算法更適用，能大大降低計算t。當信號是長序列信號時，小波分解與重構中，濾波器要補很多的零，這對信號的實時計算很不利，我們可以采用長序列快速相關卷積算法對信號進行分段后再運用FFT算法，提高運算速度。

　　4、基于算術傅里葉變換的小波變換快速算法

　　算術傅里葉變換（AFT）是1988年由Tufts和Sadasiv提出的一種用Mobius反演公式計算連續函數傅里葉系數的方法。它具有乘法運算t僅為O（N）算法簡單、并行性好的優點。根據DPT和連續函數傅里葉系數的關系，可以用AFT計算DFT。同直接算法相比，APT方法可以將DFT的計算時間減少90%，尤其是對于含有較大素因子，特別是其長度本身為素數的DFT，它的速度比傳統的FFT更快。另一方面，Mallat算法的分解和重構算法也可由DFT來計算，從而將AFT與Mallat算法聯系了起來，從而為小波變換快速算法開辟了新的途徑。

　　對于尺度

　　1）為j的快速分解算法步驟如下：

　　1）選定濾波器系數h（n）和g（n），再根據FFT的性質2，用N點的AFT分別計算出H（k）和G（k），分別取共扼，進而得到H*（k），G*（k）。

　　2）在已知cj（n）的情況下，用N點的AFT求出其DFTCj（k）

　　3）分別計算出H*（k）Cj（k），G*（k）Cj（k），即C’j（k）和D’j（k）

　　4）用N點的AFT求出C’j+1（k）和D’j+1（k）IDFT，得到C’j+1（n）和D’j+1（n）IDFT，再分別對它

　　們作二抽取，就可求出Cj+1（n）和Dj+1（n）。

　　在進行分解計算時，H（k）G（k）只要計算一次即可。重復步驟（2）一（4）可實現下一尺度小波分解，直到達到規定的尺度為止。不過要注意：尺度增加一個級別，信號長度減半。

　　2）對于尺度為j+1的快速重構算法為：

　　1）對Cj+1（n）和Dj+1（n）進行二插值，得到C’j+1（n）和D’j+1（n）;

　　2）用N點的AFT分別求出h（n）、g（n）的DFTH（k）和G（k）

　　3）用N點的AFT分別求出C’j+1（n）和D’j+1（n）的DFTC’j+1（k）和D’j+1（k）;

　　4）根據（17）式求出Cj（k），再用N點的AFT進行IDFT，可求出cj（n）。

　　5、基于Hermite插值的小波變換模極大值重構信號快速算法

　　信號在不同尺度上的小波變換模極大值包含了信號中的重要信息，因此研究如何由小波變

　　換模極大值重構信號是很有意義的。論文提出了一種基于Hermite插值多項式由二進小波變換模極大值重構信號的快速算法。數值試驗表明，與S.Mallat提出的經典交替投影算法相比，該算法可以在保證重構質量的前提下簡化計算過程，提高計算效率，計算所需時間與交替投影算法相比大大減少，是一種實用性較強的信號重構算法。

　　Hermite插值［11］方法是一種具有重節點的多項式插值方法，由于它要求在節點處滿足相應的導數條件，因此也稱為切觸差值。由于小波系數模極大值點的導數為零，這與Hermite插值對節點的導數要求不謀而合，因此我們選用Hermite插值多項式作為改進的插值方法。

　　6、強奇異積分方程小波Petrov-Galerkin快速算法

　　通過構造具有高階消失矩、小支集和半雙正交性質的分片多尺度小波基底，給出第2類強奇異積分方程的小波Petrov-Galerkin快速算法，并證明該算法收斂階達到最佳，條件數有界，計算復雜性幾乎最佳。構造配置泛函的思想，構造分片多項式空間Xn上2列具有半雙正交性的小波基，其中一列具有高階消失矩性質。