分形維數簡介

　　分形維數被譽為大自然的幾何學的分形（Fractal）理論，是現代數學的一個新分支，但其本質卻是一種新的世界觀和方法論。分維反映了復雜形體占有空間的有效性，它是復雜形體不規則性的量度。它與動力系統的混沌理論交叉結合，相輔相成。它承認世界的局部可能在一定條件下或過程中，在某一方面（形態，結構，信息，功能，時間，能量等）表現出與整體的相似性，它承認空間維數的變化既可以是離散的也可以是連續的，進而拓展了視野。

　　分形維數原理

　　fractal dimension主要描述分形最主要的參量，簡稱分維。通常歐幾里德幾何中，直線或曲線是1維的，平面或球面是2維的，具有長、寬、高的形體是 3 維的；然而對于分形如海岸線、科赫曲線、謝爾賓斯基海綿等的復雜性無法用維數等于 1、2、3 這樣的數值來描述。科赫曲線第一次變換將1英尺的每邊換成3個各長4英寸的線段，總長度變為 3×4×4/3=16 英寸；每一次變換使總長度變為乘以4/3，如此無限延續下去，曲線本身將是無限長的。這是一條連續的回線，永遠不會自我相交，回線所圍的面積是有限的，它小于一個外接圓的面積。因此科赫曲線以它無限長度擠在有限的面積之內，確實是占有空間的 ，它比1維要多，但不及2維圖形，也就是說它的維數在1和2之間，維數是分數。同樣，謝爾賓斯基海綿內部全是大大小小的空洞，表面積是無限大，而占有的 3 維空間是有限的，其維數在2和3之間。

　　圖像的分形維數研究與分析

　　1 分形基礎

　　1. 1 分形理論

　　Mandelbrot 曾經為分形下過兩個定義：（1） D（ A）》d（ A的集合 A，稱為分形集，其中 ，D（ A）為集合A的 Hausdoff 維數（或分維數），d（ A）為其拓撲維數。一般說來 ，D（ A）不是整數，而是分數;（2）部分與整體以某種形式相似的形 ，稱為分形。然而，經過理論和應用的檢驗，人們發現這兩個定義很難包括分形如此豐富的內容。實際上，對于什么是分形，到目前為止還不能給出一個確切的定義，人們通常是列出分形的一系列特性來加以說明。 分形特性有：

　　（1）分形集具有精細的結構 ，即有任意小比例的細節 ;

　　（2）分形集是如此的不規則以至它的整體和局部都不能用傳統的幾何語言描述 ;

　　（3）分形集通常有某種自相似的性質 ，可能是近似的或是統計的 ;

　　（4）一般的 ，分形集的“分形維數”（以某種方式定義） 大于它的拓撲維數 ;

　　（5）在大多數令人感興趣的情形下 ，分形集以非常簡單的方法定義 ，可能由迭代產生。

　　1. 2 分形維數

　　在歐幾里德空間 ，所有的物體的維數都是整數維的 ，而分形理論則把維數視為分數。 維數是分形幾何理論中重要基本概念之一 ，目前已經有許多維數的定義 ，主要包括 Hausdorff 維數、計盒維數（Box2counting dimension） 、修正計盒維數、填充維數等。 在實際應用中 ，通常所說的分形維數都是指計盒維數 ，而在分形理論應用研究中提出的許多維數的概念都是計盒維數的變形。

　　2 分形維數在圖像分析中的應用

　　分形理論在圖像分析中的應用是基于以下兩點為基礎的 ：一是自然界中不同種類的形態物質一般具有不同的分維數 ;二是由 A. P. Pentland 的假設 ，自然界中的分形與圖像的灰度表示之間存在著一定的對應關系

　　2. 1 分形維數在圖像分類中的應用

　　李厚強等在對航空遙感圖像進行分類時采用基于分形維數的方法計算紋理特征 ，以此來提取和分析遙感圖像的結構特征 ，并與航空遙感圖像的另一重要特征 ———光譜信息相結合 ，通過綜合應用紋理信息和光譜信息實現對遙感圖像的分析與識別。 尺度不變性是基于分形的紋理特征的一個重要特點 ，這非常適合遙感圖像分類。 現有的基于分形模型的方法是以分形維數作為紋理特征 ，在計算分形維數時 ，該文章采用 N. Sarkar 和 B. B. Chaudhuri 提出的 DBC（Differential Box Counting） 方法。 其主要思想如下。

　　將 M ×M 大小的圖像分割成 s ×s 的子塊（ M/ 2 Ε s 》 1 ，s 為整數） ，令 r = s/ M 。 將圖像想象成三維空間中的曲面 ， x ， y 表示平面位置 ， z 軸表示灰度值。 xy 平面被分割成許多s ×s的網格 ，在每個網格上 ，是一列 s ×s ×s的盒子。 設圖像灰度在第（ i ， j）網格中的最小值和最大值分別落在第 k 和第 l 個盒子中 ，則 ：

　　nr （ i ， j） = l - k + 1 （4）

　　是覆蓋第（ i ， j） 網格中的圖像所需的盒子數 ，而覆蓋整個圖像所需的盒子數 N r 為

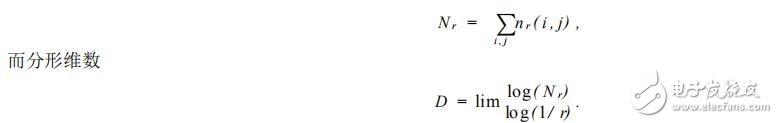
　　針對不同的 r，計算 N r ，應用最小二乘法 ，即可求得分形維數 D. 在實際應用中 ，僅以分形維數為特征 ，很難達到好的分類效果 ，于是 ，文章引入“空隙”特征的概念 ，并將高、低灰度圖像變換作為紋理特征之一 ，結合圖像的色度和飽和度 ，有效地避免了不同材料計算得出相同分形維數的情況 ，可以較為準確的對航空遙感圖像進行分類。

　　基于分形維數的圖像分類也可以應用于圖像壓縮的預處理 ，基于分形維數特征 ，將圖像分為不同的區域 ，而這一分類 ，對圖像進行進一步的壓縮編碼具有重要的指導意義。曹文倫等依據圖像灰度變化的平緩或劇烈程度 ，將圖像分為以下幾類 ：紋理、紋理邊緣、紋理邊緣平滑、邊緣平滑和平滑 ，并且分別計算以及確定了不同圖像種類的分形維數區間。 按照此區間 ，可以對待測圖像基于其分形維數進行分類。 利用分類結果 ，可以分析以及初步判斷待測圖像的空間不規則程度 ，對在進一步進行壓縮編碼具有指導意義。 如果一個物體的表面是分形的 ，則由它產生的圖像灰度表面也具有分形的性質。 基于此 ，通過 Keller 的盒維數算法完成原圖分形維數的提取。 其主要思想是：令離散灰度圖像 F是一個在三維空間中的分形曲面 ，長、寬為 R; Nε（ F） 表示邊長為ε×ε×ε的包含所要估計的圖像區域 ，其分形維數 DB 將由（7） 式決定 ：

　　將 R ，ε帶入（8） 式 ，即可求出灰度圖像 F的盒維數 DB 。 分形維數可以很好的作為圖像分析與分類的參數 ，該方法所使用的采用分形維數的圖像分類與人憑借主觀感受對圖像進行的分類相吻合。

　　李杰等在對待壓縮圖像進行預處理時 ，把標準圖像分為圖像塊 ，通過計算其分形維數 ，依據圖像塊內灰度及其變化情況 ，把圖像塊分為 3 類 ：均勻塊、中值塊和邊緣塊 ，不同種類的圖像塊反映了不同的紋理特征。 在對圖像塊分形維數特征的計算中 ，本文采用的是基于形態算子的毯子覆蓋法計算圖像塊灰度圖像的分形維數。 其主要思想是灰度圖像想象成一個在三維空間中的分形曲面 ，所要估計的圖像區域的分形維數 D 將由下面的公式確定

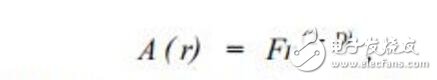
　　式中 A （ r） 為分形曲面的表面積 ， r為度量時所使用的面積元尺度 ， D為曲面的分形維數 ， F是一常數。 曲面的表面積求法如下 ：把三維空間中的所有距離曲面表面為 r的點 ，用厚度為2 r的毯子覆蓋 ，曲面的表面積就是被覆蓋的體積除以2 r，覆蓋的毯子由曲面的上表面 ur 和下表面 br 來定義 ：設曲面上點（ i ， j） 的灰度值為 g（ i ， j） ，取 r = 1 ，2 ，3 ， …， ur ， br 的值為

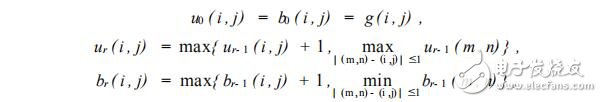
　　其中點（ m ， n） 是距離點（ i ， j） 不大于 1 的點 ，取于點（ i ， j） 的四鄰域。 該毯子的體積為 ：

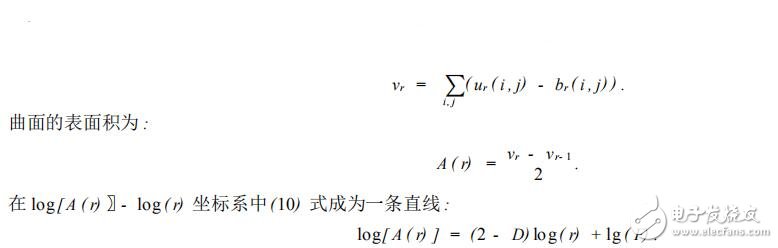
　　并在 log［ A （ r） ］2log （ r） 坐標系中做直線的最小二乘擬合 ，直線的斜率即為圖像的分形維數 D.文中引入了α，β兩個衍生參數作為分類辨別參數 ，以此來集中體現圖像塊的紋理特點。 將待測圖像塊的分形維數值與α，β相比較 ，并確定圖像塊的所屬分類 ，依據分類 ，對不同的圖像采用不同方式的壓縮編碼。 該方法基本正確的反映了圖像中的紋理分布情況。 針對圖像塊的紋理分布情況 ，采用不同的壓縮編碼 ，可以得到較好的效果.

　　2. 2 分形維數在圖像分割中的應用

　　薛笑榮等針對 SAR（合成孔徑雷達） 圖像包含相干斑噪聲 ，導致傳統方法不能很好對其分割的問題 ，考慮將 SAR 圖像的特點和分形理論相結合 ，從而提出了一種新的 SAR 圖像分割方法。 該方法首先對原始 SAR 圖像每個像元為中心取兩種不同窗口 ，計算在該兩種窗口下基于區域自選的分形維數并求均值 ，將其作為分形紋理特征。 然后根據 SAR 圖像噪聲在小波域中的分布特點對 SAR 圖像進行濾波 ，最后以 SAR 圖像分形紋理特征和濾波后的灰度組成特征向量對 SAR 圖像進行分割。 同樣是針對嚴重的噪聲干擾導致傳統方法不能很好的完成圖像分割的問題 ，彭復員等［11 ］提出通過圖像分形維數和分形常數的特征來實現對激光水下圖像紋理特征的分割。 該方法利用了毯子覆蓋法 ，并在線性擬合計算分形維數（斜率） 的同時計算分形常數（截距） ，然后對這兩個數據采用局部最佳閾值法 ，進行二維直方圖閾值分割。

　　于向軍等針對路面狀況攝像檢測過程中路面裂縫的圖像分割問題 ，提出了利用分形理論進行圖像分割的方法。 該方法根據路面裂縫圖像的自相似性 ，通過對路面裂縫的分形特征進行聚類分析來識別圖像的邊緣。 首先計算圖像的分形維數 D ，然后計算均值 mean 和方差σ。 通過以上計算可以得到一組分別表示裂縫圖像的分形維數、圖像的平均強度和圖像灰度變化的劇烈程度的特征參數數據{ D ， mean σ， }。 最后采用 K2平均法通過分裂和合并的聚類過程實現將數據點集{ D ， mean σ， }作為聚類過程的原始數據通過判定得出聚類結果 ，這樣每一小塊就對應一個類別標號 ，將這些類別標號還原到它所對應的小子塊上 ，即得分割結果圖像。 該方法不僅可以提高圖像分割的精度 ，而且顯著的減少了圖像處理的數據量和處理時間。 同樣是針對分割路面裂縫的方法 ，王華等在差分計盒方法計算圖像分形維數的基礎上 ，提出一種差分計盒方法的改進算法 ，使用該方法計算路面圖像的分形維數 ，所得的分形維數可以把簡單的閾值應用到路面裂縫的分割。 該方法將差分計盒方法計算中盒子的長度改為 1/ 2n，首先取圖像中固定大小的像素塊 ，計算該像素塊的分形維數 ，然后將像素塊在圖像上移動 ，計算像素塊覆蓋下的分形維數 ，接著畫出分形維數的直方圖。 因為小于維數 2 的圖像塊是在紋理的邊沿上 ，所以 ，在分形維數等于 2 處 ，將直方圖分開 ，則分形維數小于 2 的圖像塊就為裂縫的位置 ，從而實現了路面裂縫的圖像分割。

　　針對遙感圖像的特征提取與分割 ，鄭桂香等利用雙毯法［15 ］Double Blanket Method） 提取圖像的分形特征并用于分割。首先 ，通過比較局部分形維數偏移全局分形維數的標準差確定適合該方法的最優滑動窗口。 其次 ，提取出多尺度的特征值并建立分形維數譜。 然后 ，分析圖像中各區域的分維譜 ，選擇適當尺度的分形特征 ，利用最大似然法對圖像進行分割。 該方法可以顯著的提高遙感圖像的分割精度。 同樣是針對遙感圖像的分割問題 ，陳小梅等［16 ］針對遙感圖像的分形特點 ，采用局部分形維數進行圖像分割。 利用金字塔模型替代了局部分形計算中的窗口模板 ，從而對局部三角棱柱面法進行了改進 ，并設計了一種新的遞歸計算流程 ，有效的降低了內存存儲量。 該方法提高了基于遙感圖像紋理特征的圖像分割方法的計算速度 ，同時保留了三角棱柱面法對于分形維數計算的準確性。 但是 ，如何解決分維計算中出現的“邊緣效應”，自適應確定圖像的自相似尺度范圍以提高圖像的分割精度 ，仍然有待進一步研究

　　2. 3 分形維數在圖像邊緣檢測中的應用

　　張坤華等［17 ］通過分析 ，得出面積度量的分形參數系數 k ，并把它作為邊緣檢測分形特征。 使用地毯覆蓋法計算分形維數 ，在估計出表面積 A （ε） 后計算 k. 該方法引入自適應閾值 T = a ·max k （ i ， j） 來完成邊緣檢測與提取。 黃寰等［18 ］在針對加性高斯白噪聲的情況時 ，研究了 H 值小波變換計算方法。 而對分形參數的估計是首先濾波然后再差分 ，從而平滑和抑制噪聲 ，實現了有噪圖像的邊緣檢測。 羅強等［19 ］在進行邊緣檢測時 ，利用圖像的子圖分形結構差異和分形失真度的不同 ，采用自適應四叉樹和鄰近搜索相結合的方法 ，設定了分形編碼閾值。 在搜索子塊所對應的最佳匹配父塊的過程中 ，把與父塊的失真度大于閾值的子塊劃為邊緣 ，通過零交叉和二值化來完成圖像的邊緣提取工作。

　　SAR 圖像中包含大量的相干斑 ，且 SAR 圖像內容復雜 ，特別是自然環境中隨機變化的因素和復雜的紋理背景在很大程度上影響了邊緣檢測的準確性、適應性和實時性 ，這使得傳統的邊緣檢測方法很難取得滿意的效果。 針對以上問題 ，張紅蕾等［20 ］使用多重分形維數描述圖像的紋理。 首先計算原始 SAR 圖像離散點數據的奇異性指數 ，然后對應每一點奇異性指數計算全局多重分形奇異譜 ，最后根據判決準則區分邊緣和紋理從而實現 SAR 圖像的邊緣檢測。 該方法能夠檢測到許多局部細節 ，同時又避免出現不重要的細節 ，突出了主要的邊緣信息 ，很好的區分出 SAR 圖像的紋理和邊緣。 但是 ，如何同時使用幾個測度來提高圖像邊緣的精度 ，還有待進一步研究。

　　3 結 論

　　自然物體和人工物體的圖像在分形維數上存在著一定的差異 ，正是這個差異 ，使得分形理論和技術在圖像分析中的應用成為可能。 盒維、差分盒維、毯子維等方法 ，是目前研究較為充分的方法 ，在很多領域都有著較為廣泛的應用。 而結合小波、形態學、模式識別和神經網絡以及多重分維計算等相關技術 ，是基于分形理論的圖像分析方法的發展趨勢 ，值得進一步關注和廣泛深入研究。