基于以上概念,在SPIHT算法中,集合的分割策略如下式所示:
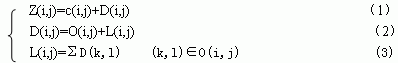
2)排序過程
編碼中使用了三個表:不重要系數表LIP(the list of insignificant pixels)、重要系數表LSP(the list of significant pixels)和不重要集合表LIS(the list of insiginificant sets)。LSP初始化為空表,LIP用最低頻子帶系數(如三級分解中的LL3、LH3、HL3、HH3中的系數)初始化,LIS用每一個空間方向樹的根結點(如三級分解中的LH3、HL3、HH3中的系數位置)來初始化。
對重要圖的確定主要是通過空間方向樹的多次分裂來實現的。一個三級空間方向樹T(i,j)在初始化時分裂成樹頭結點c(i,j)和剩余集合D(i,j),見公式(1)。對c(i,j)判斷其重要性,若重要則轉到LSP中。對集合D(i,j) 進行重要性測試,若D(i,j)是不重要的,則D(i,j)用一個符號就可以表示出來。若D(i,j)是重要的,則D(i,j)繼續分裂為兩個集合O(i,j)和L(ij),如公式(2)。對O(i,j)中的每個元素分別進行重要性測試,把重要元素轉到LSP中。對L(i,j)集合進行重要性測試,若L(i,j)不重要,則用一個符號就可以表示該集合,若L(i,j)重要,則L(i,j)分裂為四部分,每部分由相應空間方向樹的位置上的元素構成,每一部分與O(i,j)中的四個元素分別構成四棵新樹,由于每棵新樹的頭結點已經判斷,只對新樹的剩余部分也就是L(i,j)分裂出的四個集合即進行判斷,見公式(3) 。如此重復對每棵樹進行分裂和判斷直到找出每棵樹中的所有重要元素,把它們轉到LSP中。可以看到SPIHT算法對重要圖的排序是通過一系列的集合分裂完成的,即一棵樹T(i,j)分裂成頭結點元素c(i,j)和剩余部分D(i,j),對重要的D(i,j)繼續分裂成頭結點的直接四個孩子O(i,j)和剩余部分L(i,j),對重要的集合L(i,j)再繼續分裂為四棵新樹的剩余部分。
對每棵樹的分裂不是一次進行到底的,而是要按照一定的掃描順序進行。對各個子帶的掃描順序與EZW算法的掃描順序相同。對由最低頻子帶(如LL3)和頭結點構成的LIP中的元素是按從上到下、從左到右的順序進行掃描的。而對其它子帶則是按2×2的塊為單位從上到下、從左到右依次掃描。對每個2×2塊中元素還是按從上到下、對每個2×2塊中元素還是按從上到下、從左到右順序掃描。
3) 量化過程:
SPIHT采用與EZW算法相同的逐次逼近量化。
與EZW算法的比較:
SPIHT算法繼承了EZW算法中的小波系數的零樹結構,這里稱為“空間方向樹結構”。該算法不但把零樹作為一個集合,而且把剩余樹(即除去頭結點的零樹)也作為一個集合處理。如圖2,假設在HH3中的某個元素C(i,j)是重要的,而其后所對應的HH2、HH1中的元素是不重要的,則在EZW算法中第一次掃描把C(i,j)賦予符號P,對其后的所有元素形成四棵零樹ZTR(2i,2j)、ZTR(2i,2j+1)、ZTR(2i+1,2j)、ZTR(2i+1,2j+1)。共用PZZZZ五個符號表示這樣的一個結構。在SPIHT中C(i,j)即放在LIP中,又放在LIS中。對LIP中元素的比較之后把C(i,j)轉到LSP中。而對LIS比較之后發現D(i,j)是不重要的(D(i,j_)是指以(i,j)為樹根的樹除去根結點外所有的結點),可用一個符號來表示。整個結構可用兩個符號表示出來。所以該算法比EZW算法提高了壓縮率。
SPIHT算法初始化過程、細化過程類似與EZW算法,它改進了EZW 重要圖的表示方法,也就是重要系數在表中的排序信息,使得集合的表示更為精簡,從而提高了編碼效率。SPIHT算法在不同的比特率下比EZW算法的峰值信噪比都有所提高[2]。
3.集合分裂嵌入塊編碼器SPECK
3.1原理分析:
對小波變換系數的分析可以看出,在系數中存在許多的不重要系數,尤其對于高頻子帶更是如此。在EZW算法和SPIHT算法中,主要是利用樹結構來表示這些不重要系數。這兩種方法雖然利用了子帶間不重要系數的相關性,但是沒有充分利用同一子帶中不重要系數的相關性。為此 Asad 和 Pearlman提出了SPECK算法,該算法是近期嵌入式分級圖象編碼算法中性能較好的一種。
1)算法中用到的概念和定義
集合定義:LIS——不重要系數集合列表 ,用最低頻子帶系數初始化(如三級分解中的LL3)。
LSP——重要系數列表,存放重要系數以便進一步量化。
集合S——放置待處理的塊,用最低頻子帶系數初始化(如三級分解中的LL3)。
集合I——放置除了S之外的剩余塊集合,I=X-S,X是所有塊的集合。
塊:相應小波分解的每一個子帶定義一個相應的塊。塊可以是只包含單個元素,如8×8系數陣經過三級分解后對應的LL3、HL3、LH3和HH3都只包含一個元素。一般一個塊中包含22N(N=0,1,2,…,n)個元素,其中,n-1是小波分解的層數。
2)排序過程
對于只包含一個元素的塊,若重要則把它轉到LSP中,以便進行進一步量化。對于包含2N×2N個元素的塊,如果是不重要的,可以只用一個符號表示它。對于重要的塊,則要等分為四個子塊,然后從上到下、從左到右對各個子塊進行重要性判斷,對重要的子塊繼續分解,如此重復直到找出塊中所有的重要系數,并把它轉到LSP表中,以便進一步量化。
對各個塊的處理順序是與EZW算法對子帶的掃描順序是相同的,即從低頻塊(子帶)依次到高頻塊(子帶)。具體在SPECK算法中,采用一種稱為倍頻程分裂的方法,來決定各塊掃描順序。初始化時集合X由所有塊構成,集合S是由最低頻塊(如LL3)來初始化,而剩余集合I=X-S。集合I依次分解出三個最低頻的塊(如HL3,LH3,HH3)和剩余集合I。然后對剩余集合I再進行一次分裂,分解出三個次最低頻的塊(如HL2,LH2,HH2),如此重復直到把所有的塊分裂出來,直到剩余集合I變為空集。這樣就可以把各個塊依次排列,重要圖掃描就是以此順序來進行。
通過以上兩步,就可以把重要系數重要性放到表LSP中,以便下一步的逐次量化。
3)量化過程
SPECK算法的量化、求初始閾值與EZW算法相同。
SPECK算法的特點如下:①以上三種算法在掃描順序和量化過程是一樣的,差別在于對不重要系數的表示方法,EZW采用零樹結構,SPIHT采用空間方向樹,SPECK采用塊結構。SPIHT算法在一個集合中包含了更多的不重要系數,提高了壓縮率,而SPECK算法采用易于計算和并行處理的塊結構,提高了編碼速度。 ②另外,SPECK算法還有其它一些特點。需要小的動態存儲,有強的容錯性。因為塊間是獨立編碼的,在傳輸發生誤碼時,只有誤碼所在的塊受到影響。而在EZW和SPIHT中誤碼將影響到整個樹結構,對圖象的破壞較大。
 電子發燒友App
電子發燒友App





















評論