?? ?引言
在基于小波變換的圖象壓縮方案中,嵌入式零樹小波 EZW(Embedded Zerotree Wavelets)[1]編碼很好地利用小波系數(shù)的特性使得輸出的碼流具有嵌入特性。近年來,在對(duì)EZW改進(jìn)的基礎(chǔ)上,提出了許多新的性能更好的算法,如多級(jí)樹集合分裂算法(SPIHT :Set Partitioning In Hierarchical Trees)[2],集合分裂嵌入塊編碼(SPECK:Set Partitioned Embedded bloCK coder),可逆嵌入小波壓縮算法(CREW:Compression with Reversible Embedded Wavelets)[3] 。本文對(duì)這些算法進(jìn)行了原理分析、性能比較,說明了嵌入式小波圖象編碼的研究方向。
1. 嵌入式零樹小波編碼算法EZW
1. 1算法原理:
內(nèi)嵌編碼[1](embedded coding)就是編碼器將待編碼的比特流按重要性的不同進(jìn)行排序,根據(jù)目標(biāo)碼率或失真度大小要求隨時(shí)結(jié)束編碼;同樣,對(duì)于給定碼流解碼器也能夠隨時(shí)結(jié)束解碼,并可以得到相應(yīng)碼流截?cái)嗵幍哪繕?biāo)碼率的恢復(fù)圖象。內(nèi)嵌編碼中首先傳輸?shù)氖亲钪匾?a target="_blank">信息,也就是幅值最大的變換系數(shù)的位信息。圖1顯示了一個(gè)幅度值由大到小排序后的變換系數(shù)的二進(jìn)制列表。表中每一列代表一個(gè)變換系數(shù)的二進(jìn)制表示,每一行代表一層位平面,最上層為符號(hào)位,越高層的位平面的信息權(quán)重越大,對(duì)于編碼也越重要。內(nèi)嵌編碼的次序是從最重要的位(最高位)到最不重要的位(最低位)逐個(gè)發(fā)送,直到達(dá)到所需碼率后停止。
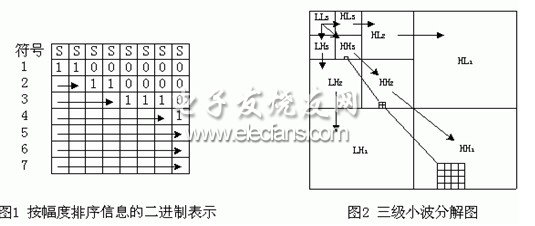
由圖1可知內(nèi)嵌編碼的輸出信息主要包括兩部分:排序信息和重要象素的位信息。其中,位信息是編碼必不可少的有效信息,對(duì)應(yīng)于表中箭頭所劃過的比特位;而排序信息則是輔助信息,按其重要性從左到右排列,反映了重要象素在原圖上的空間位置,用于恢復(fù)原始的數(shù)據(jù)結(jié)構(gòu)。因此,內(nèi)嵌算法中排序算法的優(yōu)劣和排序信息的處理決定了整個(gè)編碼算法的效率。
一副圖象經(jīng)過三級(jí)小波分解后形成了十個(gè)子帶,如圖2所示。小波系數(shù)的分布特點(diǎn)是越往低頻子帶系數(shù)值越大,包含的圖象信息越多,如圖2中的LL3子帶。而越往高頻子帶系數(shù)值越小,包含的圖象信息越少。就是在數(shù)值相同的情況下,由于低頻子帶反映的是圖象的低頻信息,對(duì)視覺比較重要,而高頻子帶反映的是圖象的高頻信息,對(duì)視覺來說不太重要。這樣對(duì)相同數(shù)值的系數(shù)選擇先傳較低頻的系數(shù)的重要比特,后傳輸較高頻系數(shù)的重要比特。正是由于小波系數(shù)具有的這些特點(diǎn),它非常適合于嵌入式圖象的編碼算法。在JPEG2000標(biāo)準(zhǔn)中以小波變換作為圖象編碼的變換方法。
EZW算法利用小波系數(shù)的特點(diǎn)較好地實(shí)現(xiàn)了圖象編碼的嵌入功能,主要包括以下三個(gè)過程:零樹預(yù)測(cè),用零樹結(jié)構(gòu)編碼重要圖,逐次逼近量化。
1) 零樹預(yù)測(cè)
一副經(jīng)過小波變換的圖象按其頻帶從低到高形成一個(gè)樹狀結(jié)構(gòu),樹根是最低頻子帶的結(jié)點(diǎn),它有三個(gè)孩子分別位于三個(gè)次低頻子帶的相應(yīng)位置,見圖2左上角,其余子帶(最高頻子帶除外)的結(jié)點(diǎn)都有四個(gè)孩子位于高一級(jí)子帶的相應(yīng)位置(由于高頻子帶分辨率增加,所以一個(gè)低頻子帶結(jié)點(diǎn)對(duì)應(yīng)有四個(gè)高頻子帶結(jié)點(diǎn),即相鄰的2×2矩陣,見圖2)。這樣圖2所示的三級(jí)小波分解就形成了深度為4的樹。
定義一個(gè)零樹的數(shù)據(jù)結(jié)構(gòu):一個(gè)小波系數(shù)x,對(duì)于一個(gè)給定的門限T,如果|x|
2) 用零樹結(jié)構(gòu)編碼重要圖
重要圖包括三種要素:即重要系數(shù)、孤立零和零樹根。其中,對(duì)于一個(gè)給定的閾值T,如果系數(shù)X本身和它的所有的子孫都小于T,則該點(diǎn)就稱為零樹根;如果系數(shù)本身小于T,但其子孫至少有一個(gè)大于或等于T,則該點(diǎn)就稱為孤立零點(diǎn)。在編碼時(shí)分別用三種符號(hào)與之對(duì)應(yīng)。當(dāng)編碼到最高分辨率層的系數(shù)時(shí),由于它們沒有子孫,零樹根不再存在,只需其余兩種符號(hào)即可。為了有利于內(nèi)嵌編碼,將重要系數(shù)的符號(hào)與重要圖一起編碼,這樣就要使用四種符號(hào):零樹根、孤立零、正重要系數(shù)、負(fù)重要系數(shù)。
3) 逐次逼近量化(Successive-Approximation Quantization,SAQ)
內(nèi)嵌編碼的核心在于采用了逐次逼近的量化方法(SAQ)。SAQ按順序使用了一系列閾值T0、T1,┄,TN-1來判決重要性,其中Ti=Ti-1/2,初始閾值T0按如下條件選擇,∣Xj∣<2T0,其中Xj表示所有變換系數(shù)。
在編(譯)碼過程中,始終保持著兩個(gè)分離的列表:主表和輔表。主表對(duì)應(yīng)于編碼中的不重要的集合或系數(shù),其輸出信息起到了恢復(fù)各重要值的空間位置結(jié)構(gòu)的作用,而輔表是編碼的有效信息,輸出為各重要系數(shù)的二進(jìn)制值。編碼分為主、輔兩個(gè)過程:在主過程中,設(shè)定閾值為Ti,按上述原理對(duì)主表進(jìn)行掃描編碼,若是重要系數(shù),則將其幅值加入輔表中,然后將該系數(shù)在數(shù)組中置為零,這樣當(dāng)閾值減小時(shí),該系數(shù)不會(huì)影響新零樹的出現(xiàn);在輔過程中,對(duì)輔表中的重要系數(shù)進(jìn)行細(xì)化,細(xì)化過程類似于比特平面編碼。對(duì)閾值Ti來說,重要系數(shù)的所在區(qū)間為[Ti,2Ti],若輔表中的重要系數(shù)位于[Ti,3Ti/2],則用符號(hào)“0”表示,否則用符號(hào)“1”表示。編碼在兩個(gè)過程中交替進(jìn)行,在每個(gè)主過程前將閾值減半。譯碼時(shí)系數(shù)的重構(gòu)值可以位于不確定區(qū)間的任意處,如果采用MMSE準(zhǔn)則,則重構(gòu)值應(yīng)位于不確定區(qū)間的質(zhì)心處。實(shí)際中為簡(jiǎn)單起見使用區(qū)間的中心作為重構(gòu)值。
1. 2算法分析:
研究表明,在圖象的低比特率編碼中,用來表示非零系數(shù)所在位置的開銷遠(yuǎn)遠(yuǎn)大于用來表示非零系數(shù)值的開銷。零樹結(jié)構(gòu)正是一種描述圖象經(jīng)過小波變換后非零數(shù)值位置的有效方法。EZW的編碼思想是不斷掃描變換后的圖象,生成多棵零樹來對(duì)圖象編碼:一棵零樹的形成需要對(duì)圖象進(jìn)行兩次掃描。在生成第一棵零樹時(shí),首先找出變換后圖象的最大絕對(duì)值系數(shù),用它對(duì)應(yīng)的T0作初始閾值,對(duì)圖象進(jìn)行第一次掃描。將圖象中絕對(duì)值小于閾值系數(shù)都看作零,然后按前面的符號(hào)定義形成零樹。在第二次掃描中,對(duì)那些絕對(duì)值大于閾值的結(jié)點(diǎn)(POS和NEG)按其絕對(duì)值是否大于閾值的1.5倍附加一個(gè)比特1或0來描述其精度。這樣做的目的是減小非零結(jié)點(diǎn)系數(shù)值的變化范圍,使其適應(yīng)下一次閾值減半后的比特附加(具體細(xì)節(jié)見文[1])。而后將閾值減半,再經(jīng)兩次掃描生成第二棵零樹,在第一次掃描生成零樹時(shí),以前已經(jīng)大于閾值的結(jié)點(diǎn)不再考慮,而第二次掃描附加比特時(shí)則要考慮以前數(shù)值較大的結(jié)點(diǎn)以保證精度。如此重復(fù)下去,不斷生成零樹,直到達(dá)到需要的編碼精度為止。
研究發(fā)現(xiàn)EZW算法存在的問題是:
(1).由于編碼時(shí)它形成多棵零樹,因而要多次掃描圖象,造成效率很低。而且每一棵樹必須在前一棵樹形成之后才能形成,所以也很難用并行算法優(yōu)化。
(2).對(duì)所有的頻域進(jìn)行等同重要度的編碼,不能充分利用小波變換的特點(diǎn)。改進(jìn)辦法之一是把最低頻子圖與其它子圖分開處理,對(duì)其進(jìn)行單獨(dú)的無失真編碼。
(3).在一棵零樹中包含的元素越多,則越有利于數(shù)據(jù)壓縮。在EZW算法中存在這樣的樹間冗余,在SPIHT算法中則進(jìn)一步利用了這種樹間冗余。
(4).通過對(duì)小波系數(shù)的分析發(fā)現(xiàn),在同一子帶中相鄰元素間有一定的相關(guān)性,尤其在高頻子帶存在大量的低值元素,所以可以通過子帶中的集合把大量的這種低值元素組織到一起,達(dá)到數(shù)據(jù)壓縮的目的。而EZW算法并沒有充分利用這種相關(guān)性。在SPECK算法中利用這種相關(guān)性達(dá)到了數(shù)據(jù)壓縮的目的。
2. 多級(jí)樹集合分裂算法 SPIHT
原理分析:
EZW算法是一種基于零樹的嵌入式圖象編碼算法,雖然在小波變換系數(shù)中,零樹是一個(gè)比較有效的表示不重要系數(shù)的數(shù)據(jù)結(jié)構(gòu),但是,在小波系數(shù)中還存在這樣的樹結(jié)構(gòu),如圖2,即它的樹根是重要的,除樹根以外的其它結(jié)點(diǎn)是不重要的。對(duì)這樣的系數(shù)結(jié)構(gòu)零樹就不是一種很有效的表示方法。A.Said和W.A.Pearlman根據(jù)Shapiro零樹編碼算法(EZW)的基本思想,提出了一種新的且性能更優(yōu)的實(shí)現(xiàn)方法,即基于分層樹集合分割排序(Set Partitioning in Hierarchical Trees,SPIHT)的編碼算法。它采用了空間方向樹(SOT:spatial orientation tree)、集合D(i,j)和L(i,j)更有效地表示這樣的系數(shù)結(jié)構(gòu),從而提高了編碼效率。
1)SPIHT算法中用到的概念
算法中的一些符號(hào)和概念說明如下:
● H:空間方向樹所有根結(jié)點(diǎn)的坐標(biāo)集合;
● Z(i,j):點(diǎn)(i,j)及其所有的后代的坐標(biāo)集合,即指空間方向樹;
● D(i,j):點(diǎn)(i,j)的所有后代(子孫)的坐標(biāo)集合,不包括(i,j)點(diǎn)本身;
● O(i,j):點(diǎn)(i,j)的直接后代(兒子)的坐標(biāo)集合,在分層塔形結(jié)構(gòu)的最高層H有O(i,j)={(i+LL,j),(i,j+LL),(i+LL,j+LL)},除此之外的結(jié)點(diǎn)有O(i,j)={(2i,2j),(2i,2j+1),(2i+1,2j), (2i+1,2j+1)},這里L(fēng)L為最高層H的尺度。
● L(i,j):點(diǎn)(i,j)除直接后代外所有后代坐標(biāo)的集合;
SPIHT算法是EZW算法的改進(jìn),它繼承了圖2所示的小波系數(shù)的零樹結(jié)構(gòu),這里稱作“空間方向樹”結(jié)構(gòu)。
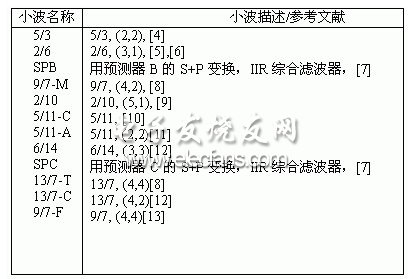
基于以上概念,在SPIHT算法中,集合的分割策略如下式所示:
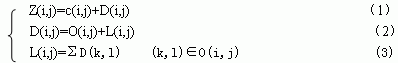
2)排序過程
編碼中使用了三個(gè)表:不重要系數(shù)表LIP(the list of insignificant pixels)、重要系數(shù)表LSP(the list of significant pixels)和不重要集合表LIS(the list of insiginificant sets)。LSP初始化為空表,LIP用最低頻子帶系數(shù)(如三級(jí)分解中的LL3、LH3、HL3、HH3中的系數(shù))初始化,LIS用每一個(gè)空間方向樹的根結(jié)點(diǎn)(如三級(jí)分解中的LH3、HL3、HH3中的系數(shù)位置)來初始化。
對(duì)重要圖的確定主要是通過空間方向樹的多次分裂來實(shí)現(xiàn)的。一個(gè)三級(jí)空間方向樹T(i,j)在初始化時(shí)分裂成樹頭結(jié)點(diǎn)c(i,j)和剩余集合D(i,j),見公式(1)。對(duì)c(i,j)判斷其重要性,若重要?jiǎng)t轉(zhuǎn)到LSP中。對(duì)集合D(i,j) 進(jìn)行重要性測(cè)試,若D(i,j)是不重要的,則D(i,j)用一個(gè)符號(hào)就可以表示出來。若D(i,j)是重要的,則D(i,j)繼續(xù)分裂為兩個(gè)集合O(i,j)和L(ij),如公式(2)。對(duì)O(i,j)中的每個(gè)元素分別進(jìn)行重要性測(cè)試,把重要元素轉(zhuǎn)到LSP中。對(duì)L(i,j)集合進(jìn)行重要性測(cè)試,若L(i,j)不重要,則用一個(gè)符號(hào)就可以表示該集合,若L(i,j)重要,則L(i,j)分裂為四部分,每部分由相應(yīng)空間方向樹的位置上的元素構(gòu)成,每一部分與O(i,j)中的四個(gè)元素分別構(gòu)成四棵新樹,由于每棵新樹的頭結(jié)點(diǎn)已經(jīng)判斷,只對(duì)新樹的剩余部分也就是L(i,j)分裂出的四個(gè)集合即進(jìn)行判斷,見公式(3) 。如此重復(fù)對(duì)每棵樹進(jìn)行分裂和判斷直到找出每棵樹中的所有重要元素,把它們轉(zhuǎn)到LSP中。可以看到SPIHT算法對(duì)重要圖的排序是通過一系列的集合分裂完成的,即一棵樹T(i,j)分裂成頭結(jié)點(diǎn)元素c(i,j)和剩余部分D(i,j),對(duì)重要的D(i,j)繼續(xù)分裂成頭結(jié)點(diǎn)的直接四個(gè)孩子O(i,j)和剩余部分L(i,j),對(duì)重要的集合L(i,j)再繼續(xù)分裂為四棵新樹的剩余部分。
對(duì)每棵樹的分裂不是一次進(jìn)行到底的,而是要按照一定的掃描順序進(jìn)行。對(duì)各個(gè)子帶的掃描順序與EZW算法的掃描順序相同。對(duì)由最低頻子帶(如LL3)和頭結(jié)點(diǎn)構(gòu)成的LIP中的元素是按從上到下、從左到右的順序進(jìn)行掃描的。而對(duì)其它子帶則是按2×2的塊為單位從上到下、從左到右依次掃描。對(duì)每個(gè)2×2塊中元素還是按從上到下、對(duì)每個(gè)2×2塊中元素還是按從上到下、從左到右順序掃描。
3) 量化過程:
SPIHT采用與EZW算法相同的逐次逼近量化。
與EZW算法的比較:
SPIHT算法繼承了EZW算法中的小波系數(shù)的零樹結(jié)構(gòu),這里稱為“空間方向樹結(jié)構(gòu)”。該算法不但把零樹作為一個(gè)集合,而且把剩余樹(即除去頭結(jié)點(diǎn)的零樹)也作為一個(gè)集合處理。如圖2,假設(shè)在HH3中的某個(gè)元素C(i,j)是重要的,而其后所對(duì)應(yīng)的HH2、HH1中的元素是不重要的,則在EZW算法中第一次掃描把C(i,j)賦予符號(hào)P,對(duì)其后的所有元素形成四棵零樹ZTR(2i,2j)、ZTR(2i,2j+1)、ZTR(2i+1,2j)、ZTR(2i+1,2j+1)。共用PZZZZ五個(gè)符號(hào)表示這樣的一個(gè)結(jié)構(gòu)。在SPIHT中C(i,j)即放在LIP中,又放在LIS中。對(duì)LIP中元素的比較之后把C(i,j)轉(zhuǎn)到LSP中。而對(duì)LIS比較之后發(fā)現(xiàn)D(i,j)是不重要的(D(i,j_)是指以(i,j)為樹根的樹除去根結(jié)點(diǎn)外所有的結(jié)點(diǎn)),可用一個(gè)符號(hào)來表示。整個(gè)結(jié)構(gòu)可用兩個(gè)符號(hào)表示出來。所以該算法比EZW算法提高了壓縮率。
SPIHT算法初始化過程、細(xì)化過程類似與EZW算法,它改進(jìn)了EZW 重要圖的表示方法,也就是重要系數(shù)在表中的排序信息,使得集合的表示更為精簡(jiǎn),從而提高了編碼效率。SPIHT算法在不同的比特率下比EZW算法的峰值信噪比都有所提高[2]。
3.集合分裂嵌入塊編碼器SPECK
3.1原理分析:
對(duì)小波變換系數(shù)的分析可以看出,在系數(shù)中存在許多的不重要系數(shù),尤其對(duì)于高頻子帶更是如此。在EZW算法和SPIHT算法中,主要是利用樹結(jié)構(gòu)來表示這些不重要系數(shù)。這兩種方法雖然利用了子帶間不重要系數(shù)的相關(guān)性,但是沒有充分利用同一子帶中不重要系數(shù)的相關(guān)性。為此 Asad 和 Pearlman提出了SPECK算法,該算法是近期嵌入式分級(jí)圖象編碼算法中性能較好的一種。
1)算法中用到的概念和定義
集合定義:LIS——不重要系數(shù)集合列表 ,用最低頻子帶系數(shù)初始化(如三級(jí)分解中的LL3)。
LSP——重要系數(shù)列表,存放重要系數(shù)以便進(jìn)一步量化。
集合S——放置待處理的塊,用最低頻子帶系數(shù)初始化(如三級(jí)分解中的LL3)。
集合I——放置除了S之外的剩余塊集合,I=X-S,X是所有塊的集合。
塊:相應(yīng)小波分解的每一個(gè)子帶定義一個(gè)相應(yīng)的塊。塊可以是只包含單個(gè)元素,如8×8系數(shù)陣經(jīng)過三級(jí)分解后對(duì)應(yīng)的LL3、HL3、LH3和HH3都只包含一個(gè)元素。一般一個(gè)塊中包含22N(N=0,1,2,…,n)個(gè)元素,其中,n-1是小波分解的層數(shù)。
2)排序過程
對(duì)于只包含一個(gè)元素的塊,若重要?jiǎng)t把它轉(zhuǎn)到LSP中,以便進(jìn)行進(jìn)一步量化。對(duì)于包含2N×2N個(gè)元素的塊,如果是不重要的,可以只用一個(gè)符號(hào)表示它。對(duì)于重要的塊,則要等分為四個(gè)子塊,然后從上到下、從左到右對(duì)各個(gè)子塊進(jìn)行重要性判斷,對(duì)重要的子塊繼續(xù)分解,如此重復(fù)直到找出塊中所有的重要系數(shù),并把它轉(zhuǎn)到LSP表中,以便進(jìn)一步量化。
對(duì)各個(gè)塊的處理順序是與EZW算法對(duì)子帶的掃描順序是相同的,即從低頻塊(子帶)依次到高頻塊(子帶)。具體在SPECK算法中,采用一種稱為倍頻程分裂的方法,來決定各塊掃描順序。初始化時(shí)集合X由所有塊構(gòu)成,集合S是由最低頻塊(如LL3)來初始化,而剩余集合I=X-S。集合I依次分解出三個(gè)最低頻的塊(如HL3,LH3,HH3)和剩余集合I。然后對(duì)剩余集合I再進(jìn)行一次分裂,分解出三個(gè)次最低頻的塊(如HL2,LH2,HH2),如此重復(fù)直到把所有的塊分裂出來,直到剩余集合I變?yōu)榭占_@樣就可以把各個(gè)塊依次排列,重要圖掃描就是以此順序來進(jìn)行。
通過以上兩步,就可以把重要系數(shù)重要性放到表LSP中,以便下一步的逐次量化。
3)量化過程
SPECK算法的量化、求初始閾值與EZW算法相同。
SPECK算法的特點(diǎn)如下:①以上三種算法在掃描順序和量化過程是一樣的,差別在于對(duì)不重要系數(shù)的表示方法,EZW采用零樹結(jié)構(gòu),SPIHT采用空間方向樹,SPECK采用塊結(jié)構(gòu)。SPIHT算法在一個(gè)集合中包含了更多的不重要系數(shù),提高了壓縮率,而SPECK算法采用易于計(jì)算和并行處理的塊結(jié)構(gòu),提高了編碼速度。 ②另外,SPECK算法還有其它一些特點(diǎn)。需要小的動(dòng)態(tài)存儲(chǔ),有強(qiáng)的容錯(cuò)性。因?yàn)閴K間是獨(dú)立編碼的,在傳輸發(fā)生誤碼時(shí),只有誤碼所在的塊受到影響。而在EZW和SPIHT中誤碼將影響到整個(gè)樹結(jié)構(gòu),對(duì)圖象的破壞較大。
4可逆嵌入小波壓縮CREW(Compression with Reversible Embedded Wavelets)
雖然EZW、SPIHT和SPECK算法提供了從無損到有損的編碼方法。編碼可以在任何地方截?cái)嗟玫揭粋€(gè)有損壓縮,也可以一直編碼直到一個(gè)準(zhǔn)無損的壓縮文件。在這里使用準(zhǔn)無損是因?yàn)檫@三種算法沒有考慮使用可逆的小波變換,即整數(shù)到整數(shù)的變換。這樣在小波變換中就引入了量化誤差。在一些場(chǎng)合要求實(shí)現(xiàn)從有損到無損的漸進(jìn)傳輸,如醫(yī)學(xué)圖象的傳輸?shù)取a槍?duì)這一要求, 可逆嵌入小波壓縮(CREW)強(qiáng)調(diào)了小波變換在漸進(jìn)圖象編碼中的重要性。
現(xiàn)在研究用于圖象編碼的可逆小波變換的越來越多,這些變換在有限算術(shù)精度意義上是可逆的,是把整數(shù)變換為整數(shù),它們是從準(zhǔn)線性小波變換得來的。正是由于這些特性,這種小波變換非常適用于無損編碼、最小內(nèi)存占用、最小計(jì)算復(fù)雜性的壓縮系統(tǒng)中。另外,這些變換對(duì)漸進(jìn)從有損到無損的圖象恢復(fù)以及有損壓縮中感興趣區(qū)的無損恢復(fù)特別有利。
對(duì)無損壓縮,圖象內(nèi)容是一個(gè)影響變換效率的重要內(nèi)容。對(duì)光滑圖象,5/11-C,5/11-A及13/7-T變換最為有效,而5/3變換對(duì)含有大量高頻信息的圖象特別合適。
表1 圖象編碼常用的可逆的小波變換
顯然,沒有一種變換對(duì)所有圖象不但具有低的計(jì)算復(fù)雜性還有好的有損和無損壓縮性能。所以,使用時(shí)要根據(jù)具體情況加以選擇。例如,在需要低的計(jì)算復(fù)雜性時(shí),5/3變換是合適的選擇,因?yàn)樗诰哂邢喈?dāng)好的無損有損壓縮性能同時(shí)具有低的計(jì)算復(fù)雜性[18]。
CREW是一個(gè)包含了有損和無損靜態(tài)圖象壓縮系統(tǒng)。它使用了一個(gè)最好小波濾波器的可逆近似。對(duì)小波系數(shù)的編碼使用了與EZW相似的Horizon方法,該方法利用了變換域中空間及頻率信息的基于內(nèi)容的編碼。它提供了最新的對(duì)醫(yī)學(xué)圖象的無損壓縮(深度大于8比特)的方法,也提供了在一個(gè)系統(tǒng)中對(duì)8比特深的圖象的從有損到無損的壓縮.
表1是一些常用的用于無損壓縮的小波濾波器,根據(jù)具體使用可以選擇。
5 結(jié)論:
由以上分析可見,在嵌入式小波編碼的研究主要從以下三個(gè)方面進(jìn)行。一是對(duì)小波系數(shù)的合理組織。研究表明,在圖象的低比特率編碼中,用來表示非零系數(shù)所在位置的開銷遠(yuǎn)遠(yuǎn)大于用來表示非零系數(shù)數(shù)值的開銷[15]。因此,內(nèi)嵌算法中排序算法的優(yōu)劣和排序信息的處理決定了整個(gè)編碼算法的效率[14]。對(duì)這些系數(shù)進(jìn)行合理排序,就可以得到更高的壓縮比如SPIHT算法以及快的編碼速度如SPECK算法。以上三種編碼算法的根本區(qū)別在于對(duì)重要圖的排序方法,如何以快的排序速度和少的重要圖編碼來尋找重要圖是嵌入式編碼算法研究的一個(gè)主要研究方向。二是從對(duì)重要系數(shù)的量化方法上進(jìn)行研究,進(jìn)一步提高數(shù)據(jù)的壓縮率。三是從小波濾波器的構(gòu)造出發(fā),找出適合具體應(yīng)用的可逆小波變換,以實(shí)現(xiàn)圖象的從有損到無損的壓縮。
 電子發(fā)燒友App
電子發(fā)燒友App





















評(píng)論