Python的科學計算包 - Numpy

numpy(Numerical Python extensions)是一個第三方的Python包，用于科學計算。這個庫的前身是1995年就開始開發(fā)的一個用于數(shù)組運算的庫。經(jīng)過了長時間的發(fā)展，基本上成了絕大部分Python科學計算的基礎包，當然也包括所有提供Python接口的深度學習框架。

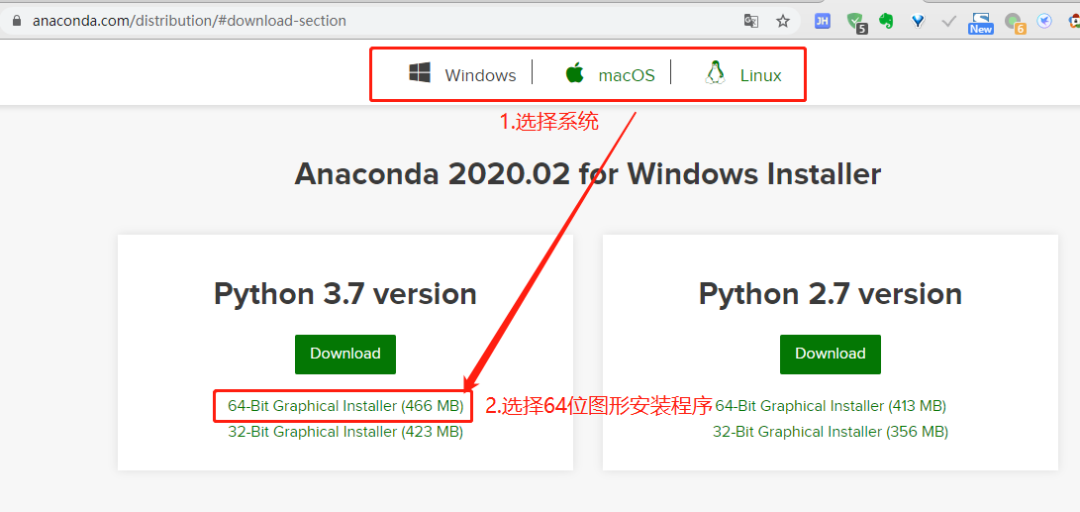
numpy在Linux下的安裝已經(jīng)在5.1.2中作為例子講過，Windows下也可以通過pip，或者到下面網(wǎng)址下載：
Obtaining NumPy & SciPy libraries

5.3.1 基本類型（array）

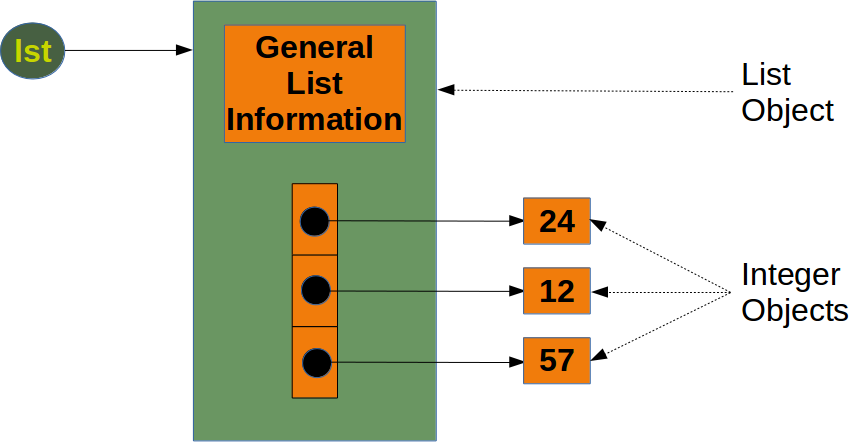
array，也就是數(shù)組，是numpy中最基礎的數(shù)據(jù)結構，最關鍵的屬性是維度和元素類型，在numpy中，可以非常方便地創(chuàng)建各種不同類型的多維數(shù)組，并且執(zhí)行一些基本基本操作，來看例子：
import numpy as np

a = [1, 2, 3, 4] #
b = np.array(a) # array([1, 2, 3, 4])
type(b) #

b.shape # (4,)
b.argmax() # 3
b.max() # 4
b.mean() # 2.5

c = [[1, 2], [3, 4]] # 二維列表
d = np.array(c) # 二維numpy數(shù)組
d.shape # (2, 2)
d.size # 4
d.max(axis=0) # 找維度0，也就是最后一個維度上的最大值，array([3, 4])
d.max(axis=1) # 找維度1，也就是倒數(shù)第二個維度上的最大值，array([2, 4])
d.mean(axis=0) # 找維度0，也就是第一個維度上的均值，array([ 2., 3.])
d.flatten() # 展開一個numpy數(shù)組為1維數(shù)組，array([1, 2, 3, 4])
np.ravel(c) # 展開一個可以解析的結構為1維數(shù)組，array([1, 2, 3, 4])

# 3x3的浮點型2維數(shù)組，并且初始化所有元素值為1
e = np.ones((3, 3), dtype=np.float)

# 創(chuàng)建一個一維數(shù)組，元素值是把3重復4次，array([3, 3, 3, 3])
f = np.repeat(3, 4)

# 2x2x3的無符號8位整型3維數(shù)組，并且初始化所有元素值為0
g = np.zeros((2, 2, 3), dtype=np.uint8)
g.shape # (2, 2, 3)
h = g.astype(np.float) # 用另一種類型表示

l = np.arange(10) # 類似range，array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
m = np.linspace(0, 6, 5)# 等差數(shù)列，0到6之間5個取值，array([ 0., 1.5, 3., 4.5, 6.])

p = np.array(
[[1, 2, 3, 4],
[5, 6, 7, 8]]
)

np.save('p.npy', p) # 保存到文件
q = np.load('p.npy') # 從文件讀取

注意到在導入numpy的時候，我們將np作為numpy的別名。這是一種習慣性的用法，后面的章節(jié)中我們也默認這么使用。作為一種多維數(shù)組結構，array的數(shù)組相關操作是非常豐富的：
import numpy as np

'''
array([[[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]],

[[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23]]])
'''
a = np.arange(24).reshape((2, 3, 4))
b = a[1][1][1] # 17

'''
array([[ 8, 9, 10, 11],
[20, 21, 22, 23]])
'''
c = a[:, 2, :]

''' 用:表示當前維度上所有下標
array([[ 1, 5, 9],
[13, 17, 21]])
'''
d = a[:, :, 1]

''' 用...表示沒有明確指出的維度
array([[ 1, 5, 9],
[13, 17, 21]])
'''
e = a[..., 1]

'''
array([[[ 5, 6],
[ 9, 10]],

[[17, 18],
[21, 22]]])
'''
f = a[:, 1:, 1:-1]

'''
平均分成3份
[array([0, 1, 2]), array([3, 4, 5]), array([6, 7, 8])]
'''
g = np.split(np.arange(9), 3)

'''
按照下標位置進行劃分
[array([0, 1]), array([2, 3, 4, 5]), array([6, 7, 8])]
'''
h = np.split(np.arange(9), [2, -3])

l0 = np.arange(6).reshape((2, 3))
l1 = np.arange(6, 12).reshape((2, 3))

'''
vstack是指沿著縱軸拼接兩個array，vertical
hstack是指沿著橫軸拼接兩個array，horizontal
更廣義的拼接用concatenate實現(xiàn)，horizontal后的兩句依次等效于vstack和hstack
stack不是拼接而是在輸入array的基礎上增加一個新的維度
'''
m = np.vstack((l0, l1))
p = np.hstack((l0, l1))
q = np.concatenate((l0, l1))
r = np.concatenate((l0, l1), axis=-1)
s = np.stack((l0, l1))

'''
按指定軸進行轉置
array([[[ 0, 3],
[ 6, 9]],

[[ 1, 4],
[ 7, 10]],

[[ 2, 5],
[ 8, 11]]])
'''
t = s.transpose((2, 0, 1))

'''
默認轉置將維度倒序，對于2維就是橫縱軸互換
array([[ 0, 4, 8],
[ 1, 5, 9],
[ 2, 6, 10],
[ 3, 7, 11]])
'''
u = a[0].transpose() # 或者u=a[0].T也是獲得轉置

'''
逆時針旋轉90度，第二個參數(shù)是旋轉次數(shù)
array([[ 3, 2, 1, 0],
[ 7, 6, 5, 4],
[11, 10, 9, 8]])
'''
v = np.rot90(u, 3)

'''
沿縱軸左右翻轉
array([[ 8, 4, 0],
[ 9, 5, 1],
[10, 6, 2],
[11, 7, 3]])
'''
w = np.fliplr(u)

'''
沿水平軸上下翻轉
array([[ 3, 7, 11],
[ 2, 6, 10],
[ 1, 5, 9],
[ 0, 4, 8]])
'''
x = np.flipud(u)

'''
按照一維順序滾動位移
array([[11, 0, 4],
[ 8, 1, 5],
[ 9, 2, 6],
[10, 3, 7]])
'''
y = np.roll(u, 1)

'''
按照指定軸滾動位移
array([[ 8, 0, 4],
[ 9, 1, 5],
[10, 2, 6],
[11, 3, 7]])
'''
z = np.roll(u, 1, axis=1)

對于一維的array所有Python列表支持的下標相關的方法array也都支持，所以在此沒有特別列出。

既然叫numerical python，基礎數(shù)學運算也是強大的：
import numpy as np

# 絕對值，1
a = np.abs(-1)

# sin函數(shù)，1.0
b = np.sin(np.pi/2)

# tanh逆函數(shù)，0.50000107157840523
c = np.arctanh(0.462118)

# e為底的指數(shù)函數(shù)，20.085536923187668
d = np.exp(3)

# 2的3次方，8
f = np.power(2, 3)

# 點積，1*3+2*4=11
g = np.dot([1, 2], [3, 4])

# 開方，5
h = np.sqrt(25)

# 求和，10
l = np.sum([1, 2, 3, 4])

# 平均值，5.5
m = np.mean([4, 5, 6, 7])

# 標準差，0.96824583655185426
p = np.std([1, 2, 3, 2, 1, 3, 2, 0])

對于array，默認執(zhí)行對位運算。涉及到多個array的對位運算需要array的維度一致，如果一個array的維度和另一個array的子維度一致，則在沒有對齊的維度上分別執(zhí)行對位運算，這種機制叫做廣播（broadcasting），言語解釋比較難，還是看例子理解：
import numpy as np

a = np.array([
[1, 2, 3],
[4, 5, 6]
])

b = np.array([
[1, 2, 3],
[1, 2, 3]
])

'''
維度一樣的array，對位計算
array([[2, 4, 6],
[5, 7, 9]])
'''
a + b

'''
array([[0, 0, 0],
[3, 3, 3]])
'''
a - b

'''
array([[ 1, 4, 9],
[ 4, 10, 18]])
'''
a * b

'''
array([[1, 1, 1],
[4, 2, 2]])
'''
a / b

'''
array([[ 1, 4, 9],
[16, 25, 36]])
'''
a ** 2

'''
array([[ 1, 4, 27],
[ 4, 25, 216]])
'''
a ** b

c = np.array([
[1, 2, 3],
[4, 5, 6],
[7, 8, 9],
[10, 11, 12]
])
d = np.array([2, 2, 2])

'''
廣播機制讓計算的表達式保持簡潔
d和c的每一行分別進行運算
array([[ 3, 4, 5],
[ 6, 7, 8],
[ 9, 10, 11],
[12, 13, 14]])
'''
c + d

'''
array([[ 2, 4, 6],
[ 8, 10, 12],
[14, 16, 18],
[20, 22, 24]])
'''
c * d

'''
1和c的每個元素分別進行運算
array([[ 0, 1, 2],
[ 3, 4, 5],
[ 6, 7, 8],
[ 9, 10, 11]])
'''
c - 1

5.3.2 線性代數(shù)模塊（linalg）

在深度學習相關的數(shù)據(jù)處理和運算中，線性代數(shù)模塊（linalg）是最常用的之一。結合numpy提供的基本函數(shù)，可以對向量，矩陣，或是說多維張量進行一些基本的運算：
import numpy as np

a = np.array([3, 4])
np.linalg.norm(a)

b = np.array([
[1, 2, 3],
[4, 5, 6],
[7, 8, 9]
])
c = np.array([1, 0, 1])

# 矩陣和向量之間的乘法
np.dot(b, c) # array([ 4, 10, 16])
np.dot(c, b.T) # array([ 4, 10, 16])

np.trace(b) # 求矩陣的跡，15
np.linalg.det(b) # 求矩陣的行列式值，0
np.linalg.matrix_rank(b) # 求矩陣的秩，2，不滿秩，因為行與行之間等差

d = np.array([
[2, 1],
[1, 2]
])

'''
對正定矩陣求本征值和本征向量
本征值為u，array([ 3., 1.])
本征向量構成的二維array為v，
array([[ 0.70710678, -0.70710678],
[ 0.70710678, 0.70710678]])
是沿著45°方向
eig()是一般情況的本征值分解，對于更常見的對稱實數(shù)矩陣，
eigh()更快且更穩(wěn)定，不過輸出的值的順序和eig()是相反的
'''
u, v = np.linalg.eig(d)

# Cholesky分解并重建
l = np.linalg.cholesky(d)

'''
array([[ 2., 1.],
[ 1., 2.]])
'''
np.dot(l, l.T)

e = np.array([
[1, 2],
[3, 4]
])

# 對不鎮(zhèn)定矩陣，進行SVD分解并重建
U, s, V = np.linalg.svd(e)

S = np.array([
[s[0], 0],
[0, s[1]]
])

'''
array([[ 1., 2.],
[ 3., 4.]])
'''
np.dot(U, np.dot(S, V))

5.3.3 隨機模塊（random）

隨機模塊包含了隨機數(shù)產(chǎn)生和統(tǒng)計分布相關的基本函數(shù)，Python本身也有隨機模塊random，不過功能更豐富，還是來看例子：
import numpy as np
import numpy.random as random

# 設置隨機數(shù)種子
random.seed(42)

# 產(chǎn)生一個1x3，[0,1)之間的浮點型隨機數(shù)
# array([[ 0.37454012, 0.95071431, 0.73199394]])
# 后面的例子就不在注釋中給出具體結果了
random.rand(1, 3)

# 產(chǎn)生一個[0,1)之間的浮點型隨機數(shù)
random.random()

# 下邊4個沒有區(qū)別，都是按照指定大小產(chǎn)生[0,1)之間的浮點型隨機數(shù)array，不Pythonic…
random.random((3, 3))
random.sample((3, 3))
random.random_sample((3, 3))
random.ranf((3, 3))

# 產(chǎn)生10個[1,6)之間的浮點型隨機數(shù)
5*random.random(10) + 1
random.uniform(1, 6, 10)

# 產(chǎn)生10個[1,6]之間的整型隨機數(shù)
random.randint(1, 6, 10)

# 產(chǎn)生2x5的標準正態(tài)分布樣本
random.normal(size=(5, 2))

# 產(chǎn)生5個，n=5，p=0.5的二項分布樣本
random.binomial(n=5, p=0.5, size=5)

a = np.arange(10)

# 從a中有回放的隨機采樣7個
random.choice(a, 7)

# 從a中無回放的隨機采樣7個
random.choice(a, 7, replace=False)

# 對a進行亂序并返回一個新的array
b = random.permutation(a)

# 對a進行in-place亂序
random.shuffle(a)

# 生成一個長度為9的隨機bytes序列并作為str返回
# 'x96x9dxd1?xe6x18xbbx9axec'
random.bytes(9)

隨機模塊可以很方便地讓我們做一些快速模擬去驗證一些結論。比如來考慮一個非常違反直覺的概率題例子：一個選手去參加一個TV秀，有三扇門，其中一扇門后有獎品，這扇門只有主持人知道。選手先隨機選一扇門，但并不打開，主持人看到后，會打開其余兩扇門中沒有獎品的一扇門。然后，主持人問選手，是否要改變一開始的選擇？

這個問題的答案是應該改變一開始的選擇。在第一次選擇的時候，選錯的概率是2/3，選對的概率是1/3。第一次選擇之后，主持人相當于幫忙剔除了一個錯誤答案，所以如果一開始選的是錯的，這時候換掉就選對了；而如果一開始就選對，則這時候換掉就錯了。根據(jù)以上，一開始選錯的概率就是換掉之后選對的概率（2/3），這個概率大于一開始就選對的概率（1/3），所以應該換。雖然道理上是這樣，但是還是有些繞，要是通過推理就是搞不明白怎么辦，沒關系，用隨機模擬就可以輕松得到答案：
import numpy.random as random

random.seed(42)

# 做10000次實驗
n_tests = 10000

# 生成每次實驗的獎品所在的門的編號
# 0表示第一扇門，1表示第二扇門，2表示第三扇門
winning_doors = random.randint(0, 3, n_tests)

# 記錄如果換門的中獎次數(shù)
change_mind_wins = 0

# 記錄如果堅持的中獎次數(shù)
insist_wins = 0

# winning_door就是獲勝門的編號
for winning_door in winning_doors:

# 隨機挑了一扇門
first_try = random.randint(0, 3)

# 其他門的編號
remaining_choices = [i for i in range(3) if i != first_try]

# 沒有獎品的門的編號，這個信息只有主持人知道
wrong_choices = [i for i in range(3) if i != winning_door]

# 一開始選擇的門主持人沒法打開，所以從主持人可以打開的門中剔除
if first_try in wrong_choices:
wrong_choices.remove(first_try)

# 這時wrong_choices變量就是主持人可以打開的門的編號
# 注意此時如果一開始選擇正確，則可以打開的門是兩扇，主持人隨便開一扇門
# 如果一開始選到了空門，則主持人只能打開剩下一扇空門
screened_out = random.choice(wrong_choices)
remaining_choices.remove(screened_out)

# 所以雖然代碼寫了好些行，如果策略固定的話，
# 改變主意的獲勝概率就是一開始選錯的概率，是2/3
# 而堅持選擇的獲勝概率就是一開始就選對的概率，是1/3

# 現(xiàn)在除了一開始選擇的編號，和主持人幫助剔除的錯誤編號，只剩下一扇門
# 如果要改變注意則這扇門就是最終的選擇
changed_mind_try = remaining_choices[0]

# 結果揭曉，記錄下來
change_mind_wins += 1 if changed_mind_try == winning_door else 0
insist_wins += 1 if first_try == winning_door else 0

# 輸出10000次測試的最終結果，和推導的結果差不多：
# You win 6616 out of 10000 tests if you changed your mind
# You win 3384 out of 10000 tests if you insist on the initial choice
print(
'You win {1} out of {0} tests if you changed your mind '
'You win {2} out of {0} tests if you insist on the initial choice'.format(
n_tests, change_mind_wins, insist_wins
)
)

5.4 Python的可視化包 – Matplotlib

Matplotlib是Python中最常用的可視化工具之一，可以非常方便地創(chuàng)建海量類型地2D圖表和一些基本的3D圖表。Matplotlib最早是為了可視化癲癇病人的腦皮層電圖相關的信號而研發(fā)，因為在函數(shù)的設計上參考了MATLAB，所以叫做Matplotlib。Matplotlib首次發(fā)表于2007年，在開源和社區(qū)的推動下，現(xiàn)在在基于Python的各個科學計算領域都得到了廣泛應用。Matplotlib的原作者John D. Hunter博士是一名神經(jīng)生物學家，2012年不幸因癌癥去世，感謝他創(chuàng)建了這樣一個偉大的庫。

安裝Matplotlib的方式和numpy很像，可以直接通過Unix/Linux的軟件管理工具，比如Ubuntu 16.04 LTS下，輸入：

>> sudo apt install python-matplotlib

或者通過pip安裝：

>> pip install matplotlib

Windows下也可以通過pip，或是到官網(wǎng)下載：

python plotting - Matplotlib 1.5.3 documentation

Matplotlib非常強大，不過在深度學習中常用的其實只有很基礎的一些功能，這節(jié)主要介紹2D圖表，3D圖表和圖像顯示。

5.4.1 2D圖表

Matplotlib中最基礎的模塊是pyplot。先從最簡單的點圖和線圖開始，比如我們有一組數(shù)據(jù)，還有一個擬合模型，通過下面的代碼圖來可視化：
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt

# 通過rcParams設置全局橫縱軸字體大小
mpl.rcParams['xtick.labelsize'] = 24
mpl.rcParams['ytick.labelsize'] = 24

np.random.seed(42)

# x軸的采樣點
x = np.linspace(0, 5, 100)

# 通過下面曲線加上噪聲生成數(shù)據(jù)，所以擬合模型就用y了……
y = 2*np.sin(x) + 0.3*x**2
y_data = y + np.random.normal(scale=0.3, size=100)

# figure()指定圖表名稱
plt.figure('data')

# '.'標明畫散點圖，每個散點的形狀是個圓
plt.plot(x, y_data, '.')

# 畫模型的圖，plot函數(shù)默認畫連線圖
plt.figure('model')
plt.plot(x, y)

# 兩個圖畫一起
plt.figure('data & model')

# 通過'k'指定線的顏色，lw指定線的寬度
# 第三個參數(shù)除了顏色也可以指定線形，比如'r--'表示紅色虛線
# 更多屬性可以參考官網(wǎng)：
plt.plot(x, y, 'k', lw=3)

# scatter可以更容易地生成散點圖
plt.scatter(x, y_data)

# 將當前figure的圖保存到文件result.png
plt.savefig('result.png')

# 一定要加上這句才能讓畫好的圖顯示在屏幕上
plt.show()

matplotlib和pyplot的慣用別名分別是mpl和plt，上面代碼生成的圖像如下：

基本的畫圖方法就是這么簡單，如果想了解更多pyplot的屬性和方法來畫出風格多樣的圖像，可以參考官網(wǎng)：

pyplot - Matplotlib 1.5.3 documentation

Customizing matplotlib

點和線圖表只是最基本的用法，有的時候我們獲取了分組數(shù)據(jù)要做對比，柱狀或餅狀類型的圖或許更合適：
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt

mpl.rcParams['axes.titlesize'] = 20
mpl.rcParams['xtick.labelsize'] = 16
mpl.rcParams['ytick.labelsize'] = 16
mpl.rcParams['axes.labelsize'] = 16
mpl.rcParams['xtick.major.size'] = 0
mpl.rcParams['ytick.major.size'] = 0

# 包含了狗，貓和獵豹的最高奔跑速度，還有對應的可視化顏色
speed_map = {
'dog': (48, '#7199cf'),
'cat': (45, '#4fc4aa'),
'cheetah': (120, '#e1a7a2')
}

# 整體圖的標題
fig = plt.figure('Bar chart & Pie chart')

# 在整張圖上加入一個子圖，121的意思是在一個1行2列的子圖中的第一張
ax = fig.add_subplot(121)
ax.set_title('Running speed - bar chart')

# 生成x軸每個元素的位置
xticks = np.arange(3)

# 定義柱狀圖每個柱的寬度
bar_width = 0.5

# 動物名稱
animals = speed_map.keys()

# 奔跑速度
speeds = [x[0] for x in speed_map.values()]

# 對應顏色
colors = [x[1] for x in speed_map.values()]

# 畫柱狀圖，橫軸是動物標簽的位置，縱軸是速度，定義柱的寬度，同時設置柱的邊緣為透明
bars = ax.bar(xticks, speeds, width=bar_width, edgecolor='none')

# 設置y軸的標題
ax.set_ylabel('Speed(km/h)')

# x軸每個標簽的具體位置，設置為每個柱的中央
ax.set_xticks(xticks+bar_width/2)

# 設置每個標簽的名字
ax.set_xticklabels(animals)

# 設置x軸的范圍
ax.set_xlim([bar_width/2-0.5, 3-bar_width/2])

# 設置y軸的范圍
ax.set_ylim([0, 125])

# 給每個bar分配指定的顏色
for bar, color in zip(bars, colors):
bar.set_color(color)

# 在122位置加入新的圖
ax = fig.add_subplot(122)
ax.set_title('Running speed - pie chart')

# 生成同時包含名稱和速度的標簽
labels = ['{} {} km/h'.format(animal, speed) for animal, speed in zip(animals, speeds)]

# 畫餅狀圖，并指定標簽和對應顏色
ax.pie(speeds, labels=labels, colors=colors)

plt.show()

在這段代碼中又出現(xiàn)了一個新的東西叫做，一個用ax命名的對象。在Matplotlib中，畫圖時有兩個常用概念，一個是平時畫圖蹦出的一個窗口，這叫一個figure。Figure相當于一個大的畫布，在每個figure中，又可以存在多個子圖，這種子圖叫做axes。顧名思義，有了橫縱軸就是一幅簡單的圖表。在上面代碼中，先把figure定義成了一個一行兩列的大畫布，然后通過fig.add_subplot()加入兩個新的子圖。subplot的定義格式很有趣，數(shù)字的前兩位分別定義行數(shù)和列數(shù)，最后一位定義新加入子圖的所處順序，當然想寫明確些也沒問題，用逗號分開即可。。上面這段代碼產(chǎn)生的圖像如下：

5.3.1 3D圖表

Matplotlib中也能支持一些基礎的3D圖表，比如曲面圖，散點圖和柱狀圖。這些3D圖表需要使用mpl_toolkits模塊，先來看一個簡單的曲面圖的例子：
import matplotlib.pyplot as plt
import numpy as np

# 3D圖標必須的模塊，project='3d'的定義
from mpl_toolkits.mplot3d import Axes3D

np.random.seed(42)

n_grids = 51 # x-y平面的格點數(shù)
c = n_grids / 2 # 中心位置
nf = 2 # 低頻成分的個數(shù)

# 生成格點
x = np.linspace(0, 1, n_grids)
y = np.linspace(0, 1, n_grids)

# x和y是長度為n_grids的array
# meshgrid會把x和y組合成n_grids*n_grids的array，X和Y對應位置就是所有格點的坐標
X, Y = np.meshgrid(x, y)

# 生成一個0值的傅里葉譜
spectrum = np.zeros((n_grids, n_grids), dtype=np.complex)

# 生成一段噪音，長度是(2*nf+1)**2/2
noise = [np.complex(x, y) for x, y in np.random.uniform(-1,1,((2*nf+1)**2/2, 2))]

# 傅里葉頻譜的每一項和其共軛關于中心對稱
noisy_block = np.concatenate((noise, [0j], np.conjugate(noise[::-1])))

# 將生成的頻譜作為低頻成分
spectrum[c-nf:c+nf+1, c-nf:c+nf+1] = noisy_block.reshape((2*nf+1, 2*nf+1))

# 進行反傅里葉變換
Z = np.real(np.fft.ifft2(np.fft.ifftshift(spectrum)))

# 創(chuàng)建圖表
fig = plt.figure('3D surface & wire')

# 第一個子圖，surface圖
ax = fig.add_subplot(1, 2, 1, projection='3d')

# alpha定義透明度，cmap是color map
# rstride和cstride是兩個方向上的采樣，越小越精細，lw是線寬
ax.plot_surface(X, Y, Z, alpha=0.7, cmap='jet', rstride=1, cstride=1, lw=0)

# 第二個子圖，網(wǎng)線圖
ax = fig.add_subplot(1, 2, 2, projection='3d')
ax.plot_wireframe(X, Y, Z, rstride=3, cstride=3, lw=0.5)

plt.show()

這個例子中先生成一個所有值均為0的復數(shù)array作為初始頻譜，然后把頻譜中央部分用隨機生成，但同時共軛關于中心對稱的子矩陣進行填充。這相當于只有低頻成分的一個隨機頻譜。最后進行反傅里葉變換就得到一個隨機波動的曲面，圖像如下：

3D的散點圖也是常常用來查看空間樣本分布的一種手段，并且畫起來比表面圖和網(wǎng)線圖更加簡單，來看例子：
import matplotlib.pyplot as plt
import numpy as np

from mpl_toolkits.mplot3d import Axes3D

np.random.seed(42)

# 采樣個數(shù)500
n_samples = 500
dim = 3

# 先生成一組3維正態(tài)分布數(shù)據(jù)，數(shù)據(jù)方向完全隨機
samples = np.random.multivariate_normal(
np.zeros(dim),
np.eye(dim),
n_samples
)

# 通過把每個樣本到原點距離和均勻分布吻合得到球體內均勻分布的樣本
for i in range(samples.shape[0]):
r = np.power(np.random.random(), 1.0/3.0)
samples[i] *= r / np.linalg.norm(samples[i])

upper_samples = []
lower_samples = []

for x, y, z in samples:
# 3x+2y-z=1作為判別平面
if z > 3*x + 2*y - 1:
upper_samples.append((x, y, z))
else:
lower_samples.append((x, y, z))

fig = plt.figure('3D scatter plot')
ax = fig.add_subplot(111, projection='3d')

uppers = np.array(upper_samples)
lowers = np.array(lower_samples)

# 用不同顏色不同形狀的圖標表示平面上下的樣本
# 判別平面上半部分為紅色圓點，下半部分為綠色三角
ax.scatter(uppers[:, 0], uppers[:, 1], uppers[:, 2], c='r', marker='o')
ax.scatter(lowers[:, 0], lowers[:, 1], lowers[:, 2], c='g', marker='^')

plt.show()

這個例子中，為了方便，直接先采樣了一堆3維的正態(tài)分布樣本，保證方向上的均勻性。然后歸一化，讓每個樣本到原點的距離為1，相當于得到了一個均勻分布在球面上的樣本。再接著把每個樣本都乘上一個均勻分布隨機數(shù)的開3次方，這樣就得到了在球體內均勻分布的樣本，最后根據(jù)判別平面3x+2y-z-1=0對平面兩側樣本用不同的形狀和顏色畫出，圖像如下：

5.3.1 圖像顯示

Matplotlib也支持圖像的存取和顯示，并且和OpenCV一類的接口比起來，對于一般的二維矩陣的可視化要方便很多，來看例子：
import matplotlib.pyplot as plt

# 讀取一張小白狗的照片并顯示
plt.figure('A Little White Dog')
little_dog_img = plt.imread('little_white_dog.jpg')
plt.imshow(little_dog_img)

# Z是上小節(jié)生成的隨機圖案，img0就是Z，img1是Z做了個簡單的變換
img0 = Z
img1 = 3*Z + 4

# cmap指定為'gray'用來顯示灰度圖
fig = plt.figure('Auto Normalized Visualization')
ax0 = fig.add_subplot(121)
ax0.imshow(img0, cmap='gray')

ax1 = fig.add_subplot(122)
ax1.imshow(img1, cmap='gray')

plt.show()
這段代碼中第一個例子是讀取一個本地圖片并顯示，第二個例子中直接把上小節(jié)中反傅里葉變換生成的矩陣作為圖像拿過來，原圖和經(jīng)過乘以3再加4變換的圖直接繪制了兩個形狀一樣，但是值的范圍不一樣的圖案。顯示的時候imshow會自動進行歸一化，把最亮的值顯示為純白，最暗的值顯示為純黑。這是一種非常方便的設定，尤其是查看深度學習中某個卷積層的響應圖時。得到圖像如下：

只講到了最基本和常用的圖表及最簡單的例子，更多有趣精美的例子可以在Matplotlib的官網(wǎng)找到：
Thumbnail gallery - Matplotlib 1.5.3 documentation