秘笈十 輕松估計負載瞬態響應

　　本篇電源設計小貼士介紹了一種通過了解控制帶寬和輸出濾波器電容特性估算電源瞬態響應的簡單方法。該方法充分利用了這樣一個事實，即所有電路的閉環輸出阻抗均為開環輸出阻抗除以 1 加環路增益，或簡單表述為：

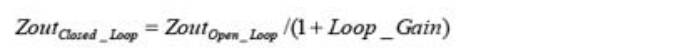
　　圖10.1以圖形方式說明了上述關系，兩種阻抗均以dB-Ω或20*log ［Z］為單位。在開環曲線上的低頻率區域內，輸出阻抗取決于輸出電感阻抗和電感。當輸出電容和電感發生諧振時，形成峰值。高頻阻抗取決于電容輸出濾波器特性、等效串聯電阻 （ESR） 以及等效串聯電感 （ESL）。將開環阻抗除以1加環路增益即可計算得出閉環輸出阻抗。

　　由于該圖形以對數表示，即簡單的減法，因此在增益較高的低頻率區域阻抗會大大降低；在增益較少的高頻率區域閉環和開環阻抗基本上是一樣的。在此需要說明如下要點：1）峰值環路阻抗出現在電源交叉頻率附近，或出現在環路增益等于1（或0dB） 的地方； 以及2） 在大部分時間里， 電源控制帶寬都將會高于濾波器諧振，因此峰值閉環阻抗將取決于交叉頻率時的輸出電容阻抗。

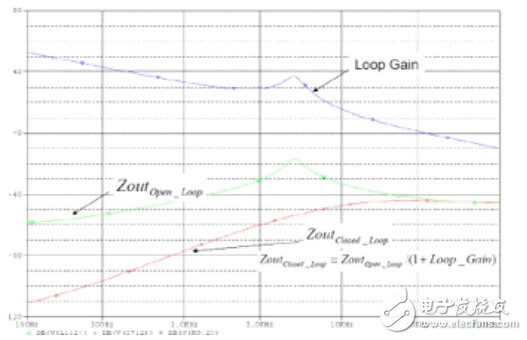
　　圖10.1閉環輸出阻抗峰值Zout出現在控制環路交叉頻率處

　　一旦知道了峰值輸出阻抗，就可通過負載變動幅度與峰值閉環阻抗的乘積來輕松估算瞬態響應。有幾點注意事項需要說明一下，由于低相位裕度會引起峰化，因此實際的峰值可能會更高些。 然而， 就快速估計而言， 這種影響可以忽略不計 ［1］ 。第二個需要注意的事項與負載變化幅度上升有關。如果負載變化幅度變化緩慢較低），則響應取決于與上升時間有關的低頻率區域閉環輸出阻抗；如果負載變化幅度變化極為快速， 則輸出阻抗將取決于輸出濾波器ESL。 如果確實如此， 則可能需要更多的高頻旁通。最后，就極高性能的系統而言，電源的功率級可能會限制響應時間，即電感器中的電流可能不能像控制環路期望的那樣快速響應，這是因為電感和施加的電壓會限制電流轉換速率。

　　下面是一個如何使用上述關系的示例。 問題是根據200kHz開關電源10amp變化幅度允許范圍內的50mV 輸出變化挑選一個輸出電容。所允許的峰值輸出阻抗為：

　　Zout=50mV/10 amps或5毫歐。這就是最大允許輸出電容ESR。接下來就是建立所需的電容。 幸運的是， ESR和電容均為正交型， 可單獨處理。 一個高 （Aggressive） 電源控制環路帶寬可以是開關頻率的1/6或30 kHz。于是在30 kHz 時輸出濾波電容就需要一個不到5毫歐的電抗， 或高于1000uF的電容。 圖10.2顯示了在5毫歐ESR、 1000uF電容以及30kHz 電壓模式控制條件時這一問題的負載瞬態仿真。就校驗這一方法是否有效的10amp負載變動幅度而言，輸出電壓變化大約為52mV。

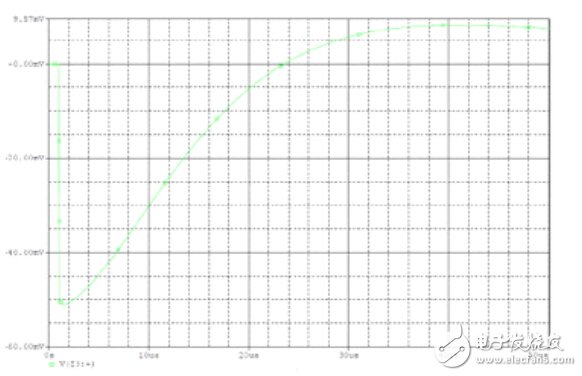
　　圖 10.2 仿真校驗估計負載瞬態性能

　　秘笈十一 解決電源電路損耗問題

　　您是否曾詳細計算過設計中的預計組件損耗，結果卻發現與實驗室測量結果有較大出入呢？本電源設計小貼士介紹了一種簡便方法，以幫助您消除計算結果與實際測量結果之間的差異。該方法基于泰勒級數展開式，其中規定（在賦予一定自由條件下）任何函數都可分解成一個多項式，如下所示：

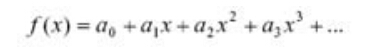
?????? 如果意識到電源損耗與輸出電流相關 （可用輸出電流替換X） ， 那么系數項就能很好地與不同來源的電源功率損耗聯系起來。例如，ao代表諸如柵極驅動、偏壓電源和磁芯的固定開銷損耗以及功率晶體管Coss充電與放電之類的損耗。這些損耗與輸出電流無關。第二項相關聯的損耗a1直接與輸出電流相關，其典型表現為輸出二極管損耗和開關損耗。在輸出二極管中，大多數損耗是由于結電壓引起的，因此損耗會隨著輸出電流成比例地增加。

　　類似地，開關損耗可通過輸出電流關聯項與某些固定電壓的乘積近似得出。第三項很容易被識別為傳導損耗。 其典型表現為 FET 電阻、 磁性布線電阻和互聯電阻中的損耗。高階項可能在計算非線性損耗（如磁芯損耗）時有用。只有在考慮前三項情況下才能得出有用結果。

　　計算三項系數的一種方法是測量三個工作點的損耗并成矩陣求解結果。如果損耗測量結果其中一項是在無負載的工況下得到 （即所有損耗均等于第一項系數a0） ，那么就能簡化該解決方法。隨后問題簡化至容易求解的兩個方程式和兩個未知數。一旦計算出系數，即可構建出類似于圖11.1、顯示三種損耗類型的損耗曲線。該曲線在消除測量結果和計算結果之間的偏差時大有用處，并且有助于確定能夠提高效率的潛在區域。例如，在滿負載工況下，圖 1中的損耗主要為傳導損耗。為了提高效率，就需要降低 FET 電阻、電感電阻和互聯電阻。

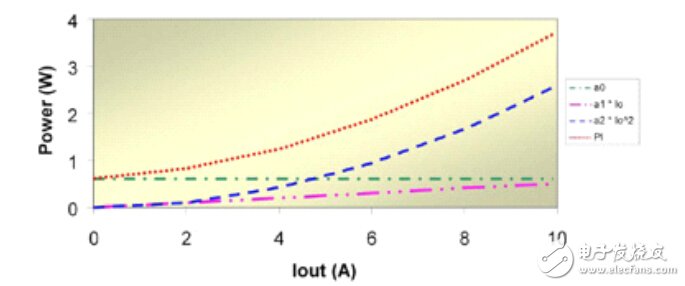
　　圖11.1：功率損耗組件與二次項系數相匹配

　　實際損耗與三項式之間的相關性非常好。圖11.2對同步降壓穩壓器的測量數據與曲線擬合數據進行了對比。我們知道，在基于求解三個聯立方程組的曲線上將存在三個重合點。對于曲線的剩余部分，兩個曲線之間的差異小于2%。由于工作模式（如連續或非連續）不同、脈沖跳頻或變頻運行等原因，其他類型的電源可能很難以如此匹配。 這種方法并非絕對可靠， 但是有助于電源設計人員理解實際電路損耗情況。

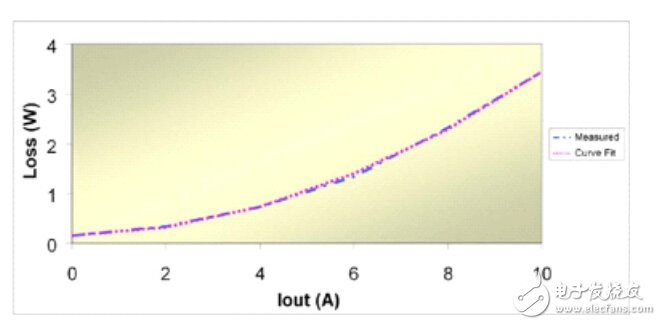
　　圖11.2 前三個損耗項提供了與測量值良好的相關性

　　秘笈十二 電源效率最大化

　　在《電源設計秘笈11》中，我們討論了如何利用泰勒級數 （Taylor series） 查找電源中的損耗源。在本篇電源設計秘笈中，我們將討論如何使用相同的級數最大化特定負載電流的電源效率。在《電源設計秘笈11》中，我們建議使用如下輸出電流函數來計算電源損耗：

　　下一步是利用上述簡單表達式，并將其放入效率方程式中：

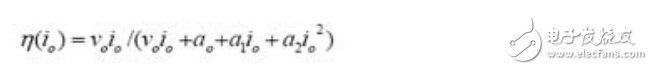
　　這樣，輸出電流的效率就得到了優化（具體論證工作留給學生去完成）。這種優化可產生一個有趣的結果。當輸出電流等于如下表達式時，效率將會最大化。

?????? 需要注意的第一件事是，a1項對效率達到最大時的電流不產生影響。這是由于它與損耗相關，而上述損耗又與諸如二極管結點的輸出電流成比例關系。因此，當輸出電流增加時，上述損耗和輸出功率也會隨之增加，并且對效率沒有影響。需要注意的第二件事是，最佳效率出現在固定損耗和傳導損耗相等的某個點上。這就是說， 只要控制設置a0和a2值的組件， 便能夠獲得最佳效率。 還是要努力減小a1的值，并提高效率。控制該項所得結果對所有負載電流而言均相同，因此如其他項一樣沒有出現最佳效率。a1項的目標是在控制成本的同時達到最小化。

　　表1概括總結了各種電源損耗項及其相關損耗系數， 該表提供了一些最佳化電源效率方面的折中方法。例如，功率MOSFET導通電阻的選擇會影響其柵極驅動要求及Coss損耗和潛在的緩沖器損耗。低導通電阻意味著，柵極驅動、Coss和緩沖器損耗逆向增加。因此，您可通過選擇 MOSFET 來控制a0和a2。

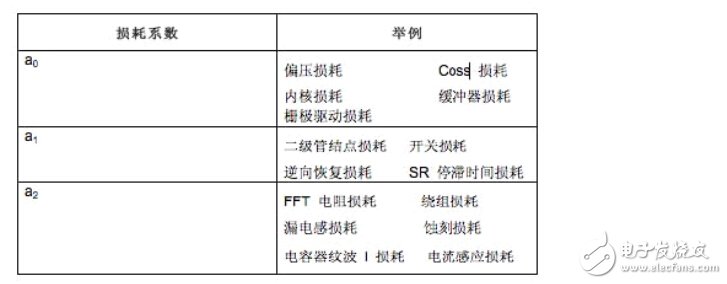
　　表1 損耗系數及相應的電源損耗

　　代數式下一位將最佳電流代回到效率方程式中，解得最大效率為：

　　需要最小化該表達式中的最后兩項， 以最佳化效率。 a1 項很簡單， 只需對其最小化即可。末尾項能夠實現部分優化。如果假設 MOSFET 的 Coss 和柵極驅動功率與其面積相關， 同時其導通電阻與面積成反比， 則可以為它選擇最佳面積 （和電阻） 。

　　圖12.1顯示了裸片面積的優化結果。裸片面積較小時，MOSFET的導通電阻變為效率限制器。隨著裸片面積增加，驅動和Coss損耗也隨之增加，

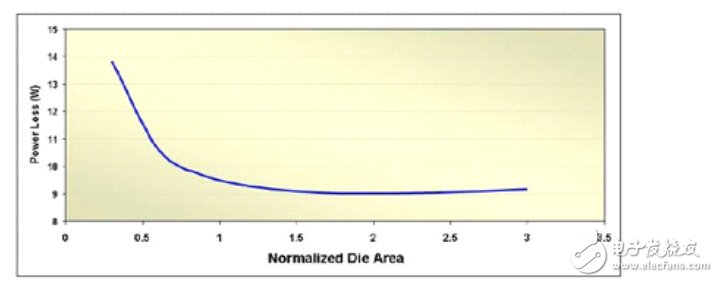
　　圖12.1 調節 MOSFET 裸片面積來最小化滿負載功率損耗

　　圖12.2是圍繞圖12.1最佳點的三種可能設計效率圖。圖中分別顯示了三種設計的正常裸片面積。輕負載情況下，較大面積裸片的效率會受不斷增加的驅動損耗影響，而在重負載條件下小尺寸器件因高傳導損耗而變得不堪重負。這些曲線代表裸片面積和成本的三比一變化，注意這一點非常重要。正常芯片面積設計的效率只比滿功率大面積設計的效率稍低一點，而在輕載條件下（設計常常運行在這種負載條件下）則更高

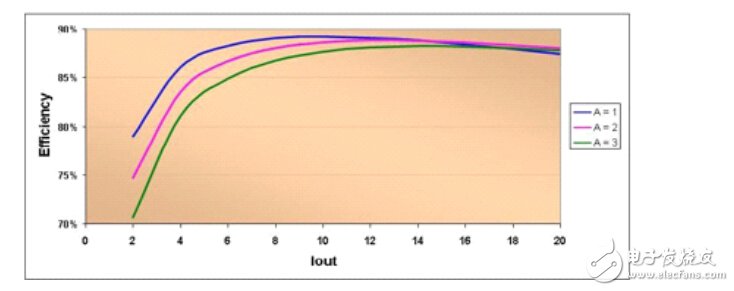
　　圖 12.2 效率峰值出現在滿額定電流之前

?